
Example Hodr S,=∫yg,w,dr=[S]* 中=C1+C2Ψ2 6= Soodr =∫y,wdr=Sn 「pdr=∫(cy,+c2y2)'(c4,+c22)dr =∫(G2441+cc4iw2+cc441+c22')dr =∫(G4,+2cc,4i2+c,)dr =q+2cc,S2+6 (S=∫yiy,dr=S) =c12S1+2cc2S2+022S2 (S11=S22=1) ∫pidr=∫(c,+c,4)广(cw4+c业,)dr =∫(cwa4+cc4ay2+ccy,户ay4,+c'w,iw)dr =c2H1+2cc,H2+c22H2 (H,=Hr=∫y,Awdr)
) ˆ 2 ( ) ˆ ˆ ˆ ˆ ( ( ) ˆ ( ) ˆ 2 ( 1 ) 2 ( ) ( 2 ) ( ) ( ) ( ) ˆ * 22 2 11 1 2 12 2 2 1 2 * 2 2 1 2 * 2 1 2 2 * 1 1 2 1 * 1 2 1 1 1 2 2 * 1 1 2 2 * 22 11 22 2 11 1 2 12 2 2 1 ji 2 * 1 2 12 2 2 1 2 * 2 2 2 2 * 1 1 2 1 * 1 2 1 2 * 2 2 1 2 * 2 1 2 2 * 1 1 2 1 * 1 2 1 1 1 2 2 * 1 1 2 2 * * * 1 1 2 2 c H c c H c H H H H d c H c c H c c H c H d H d c c H c c d c S c c S c S S S c c c S c S d S c c c c d c c c c c c d d c c c c d d H d c c ij ji i j ij i j = Example i j ji ij i j ij d S S d S * * [ ] *

let cHu+2cc,Hu+c;H=y c'Su+2cc,Sn+e2Sx x make E→Eo 0=e-10y-yx Oc x Oc x20c 2eha+2eHe-¥2as,+2cs.) 2cH1+2cH.)+256+2c5+2cSe=0 c12S1+2cc2S2+c22S2 (2cH1+2c2H12)-E(2cS1+2c2S2)=0 (cH1+c2H12)-E(cS11+c2S12)=0 (H1-ES1)c+(H2-ES2)c2=0 () same as 08 0s 8c2 (H21-ES21)c1+(H2-ES2)c2=0 (2)
( ) ( ) 0 (2) 0 ( ) ( ) 0 (1) ( ) ( ) 0 (2 2 ) (2 2 ) 0 (2 2 ) 0 22 (2 2 ) (2 2 ) (2 2 ) 1 1 0 2 2 21 21 1 22 22 2 2 11 11 1 12 12 2 1 11 2 12 1 11 2 12 1 11 2 12 1 11 2 12 1 11 2 12 22 2 11 1 2 12 2 2 1 22 2 11 1 2 12 2 2 1 1 11 2 12 1 11 2 12 2 1 11 2 12 1 2 1 1 0 22 2 11 1 2 12 2 2 1 22 2 11 1 2 12 2 2 1 H ES c H ES c c same as H ES c H ES c c H c H E c S c S c H c H E c S c S c S c S c S c c S c S c H c c H c H c H c H c S c S x y c H c H x c x x y c y c x make E x y c S c c S c S c H c c H c H let

seqular equation made equation resolved(G,C2≠O) Hu-ESu H12-ES12 =0 H21-ES21 H22-ES22 get E→get C1,C2get p The algebraic equation has 2 roots,E and E2. =C1+C22+.+CnΨn Hu-ESu H12-ES2 ..Hin-ESun H21-ES21H22-ES2 H2n-ES2n =0 Hn-ESn Hn2-ES2 .. Hm-ESm The algebraic equation has n roots,which can be shown to be real. Arranging these roots in order of increasing value:E<E2<...<E
get E get c c get H ES H ES H ES H ES made equation resolved c c seqular equation 1 2 21 21 22 22 11 11 12 12 1 2 , 0 ( , 0) 0 ... . . ... . . . ... . ... ... ... 1 1 2 2 21 21 22 22 2 2 11 11 12 12 1 1 1 1 2 2 n n n n nn nn n n n n n n H ES H ES H ES H ES H ES H ES H ES H ES H ES c c c The algebraic equation has n roots, which can be shown to be real. Arranging these roots in order of increasing value: E1 E2… En. The algebraic equation has 2 roots, E1 and E2

From the variation theorem,we know that the lowest value of root (W)is the upper bound for the system's ground-state energy. ESWI Moreover,it can be proved that the linear variation method provides upper bounds to the energies of the lowest n states of the system. E2≤Wz,E3≤W3,…,En≤Wn We use the roots as approximations to the energies of the lowest states If approximation to the energies of more states are wanted,we add more functions/to the trial function. The addition of more functions f can be shown to increase the accuracy of the previously calculated energies
• From the variation theorem, we know that the lowest value of root (W1) is the upper bound for the system’s ground-state energy. E 1 W 1 • Moreover, it can be proved that the linear variation method provides upper bounds to the energies of the lowest n states of the system. • We use the roots as approximations to the energies of the lowest states. • If approximation to the energies of more states are wanted, we add more functions fk to the trial function . • The addition of more functions fk can be shown to increase the accuracy of the previously calculated energies. E 2 W2, E 3 W3, … , En W n
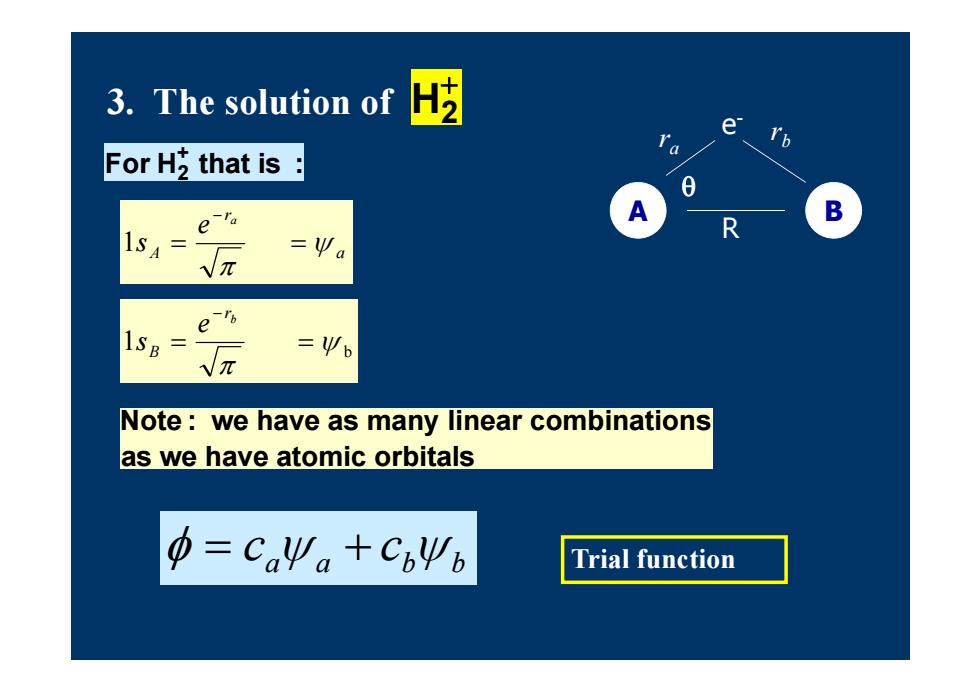
3.The solution of t H For H2 that is 0 e-ra A B D 1S4= -Wa Vπ e √元 =业6 Note:we have as many linear combinations as we have atomic orbitals 中=CaΨ。+CbVΨb Trial function
3. The solution of H2 A B e- r r b a R For H2+ that is : Note : we have as many linear combinations as we have atomic orbitals a r A a e s 1 b 1 br B e s a a b b c c Trial function