
Chap 4:lattice dynamics and lattice capacity Objectives At the end of this Chapter,you should: 1.Know the dispersion relation of 1D monoatom chain and diatom chain. 2.Know the difference between acoustic branch and optic branch. 3.Understand the concept of density of states. 4.Know the capacity difference between Eistein modes and Debye modes. 5.Establish the concept of phonons. 6.Understand the anharmonic effects
Chap 4: lattice dynamics and lattice capacity Objectives At the end of this Chapter, you should: 1. Know the dispersion relation of 1D monoatom chain and diatom chain. 2. Know the difference between acoustic branch and optic branch . 3. Understand the concept of density of states. 4. Know the capacity difference between Eistein modes and Debye modes. 5. Establish the concept of phonons. 6. Understand the anharmonic effects

4.1 Normal Modes of Vibration 4.1.1 One dimensional model 1:The Monatomic Chain Consider a Monatomic Chain of Identical Atoms with nearest-neighbor,"Hooke's Law"type forces(F=-kx) between the atoms.Aforce-spring model,with masses m spring constants K. (+1)a(+2a 1(m2)a m-1)a This is the simplest possible solid.Assume that the chain contains a very large number (N->oo)of atoms with identical masses m. Let the atomic separation be a distance a.we must Assume that the atoms move only in a direction parallel to the chain,and that only nearest-neighbours interact with each other
4.1 Normal Modes of Vibration 4.1.1 One dimensional model 1: The Monatomic Chain • Consider a Monatomic Chain of Identical Atoms with nearest-neighbor,“Hooke’s Law” type forces (F = - kx) between the atoms. Aforce-spring model, with masses m & spring constants K. • This is the simplest possible solid.Assume that the chain contains a very large number (N → ) of atoms with identical masses m. Let the atomic separation be a distance a. we must Assume that the atoms move only in a direction parallel to the chain, and that only nearest-neighbours interact with each other
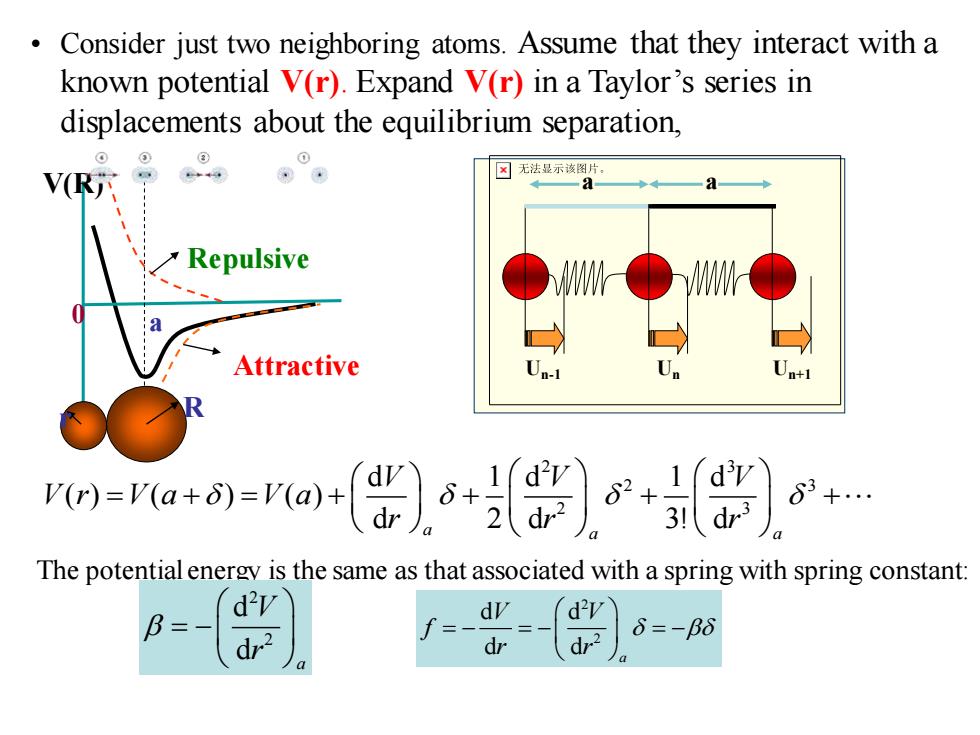
Consider just two neighboring atoms.Assume that they interact with a known potential V(r).Expand V(r)in a Taylor's series in displacements about the equilibrium separation, V(R苏 ☒无法显示该图片 Repulsive Attractive Un+1 13T V(r)=V(a+δ)=V(a)+ dr 63+. (d2 2 31dr3 The potential energy is the same as that associated with a spring with spring constant: d" B= 6=-B6 dr dr
• Consider just two neighboring atoms. Assume that they interact with a known potential V(r). Expand V(r) in a Taylor’s series in displacements about the equilibrium separation, The potential energy is the same as that associated with a spring with spring constant: r R V(R) 0 a Repulsive Attractive 2 3 2 3 2 3 d 1 d 1 d ( ) ( ) ( ) d 2 d 3! d a a a V V V V r V a V a r r r = + = + + + + a a Un-1 Un Un+1 2 2 d d d d a V V f r r = − = − = − 2 2 d d a V r = −

n=f+f方=-B(4n-+)-B(4,-n1)=B(41+4n1-24n) dw=B(4+4-2n.) m The Equation of Motion ofeach atom is of this form.Only the value of 'n'changes. 。Assume Lng Aeflo-nag) 2π q A,amplitude;o,frequency;q,wavenumber;A,wavelength -mo2=B(e-iag +eiag-2)=2B(cosaq-1) 0=21 m 2 max m The only allowed vibration frequencies o must be related to the wavenumber in this way."Phonon Dispersion Relation"for the chain,even though these are classical lattice vibrations in the classical theory
The Equation of Motion of each atom is of this form. Only the value of ‘n’ changes. ( ) ( ) ( ) f f f n n n n n n n n = + = − − − − = + − 1 2 1 1 1 1 + − + − 2 ( ) 2 2 1 1 d 2 d n n n n u m t = + − + − • Assume 1 2 sin 2 aq m = ( ) ( ) 2 2 2 cos 1 iaq iaq m e e aq − − = + − = − ( ) nq i t naq Ae − = 2 q = A, amplitude; ω, frequency; q, wavenumber;λ,wavelength The only allowed vibration frequencies ω must be related to the wavenumber in this way. “Phonon Dispersion Relation” for the chain, even though these are classical lattice vibrations in the classical theory
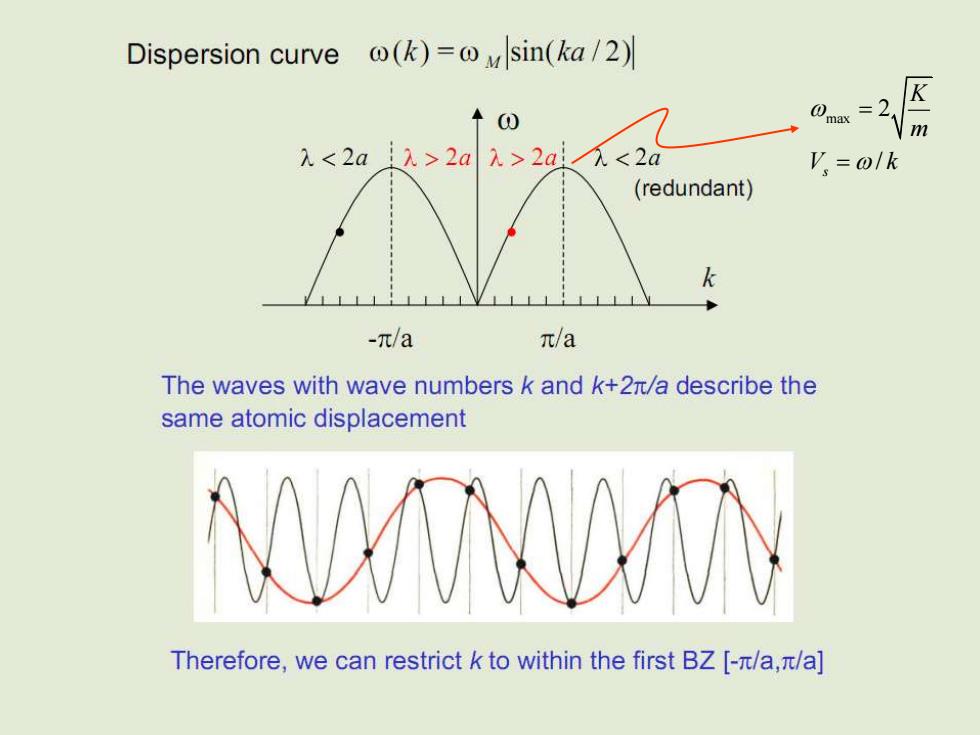
Dispersion curve (k)=sin(ka/2) ↑0 @max =2 m λ<2a1>2aλ>2a<2a V,=olk (redundant) -n/a n/a The waves with wave numbers k and k+2n/a describe the same atomic displacement Therefore,we can restrict k to within the first BZ [-/a,/a]
max 2 / s K m V k = =