
5.3 Nearly Free Electron The potential of electron is weaker than the kinetics of electron, and the motion could be seen as almost free.So,free electron motion is supposed to be the zeroth order approximation and the influence of periodical potential is regarded as the perturbation.at the same time,the motion must also obeys the symmetry condition This model is called empty lattice model. potential U ion core 1D periodical potential field for the electrons in the crystal
5.3 Nearly Free Electron The potential of electron is weaker than the kinetics of electron, and the motion could be seen as almost free. So, free electron motion is supposed to be the zeroth order approximation and the influence of periodical potential is regarded as the perturbation. at the same time, the motion must also obeys the symmetry condition. This model is called empty lattice model. 1D periodical potential field for the electrons in the crystal

for the case of 1D,the state function and energy for the empty lattice model should be: 1 2m where 0 indicates the solution with no perturbation.The relation between energy and wave vector is parabolic.Considering the requirement of symmetry,it is splitted into many parts.The energy of any two equivalent points could be the same by translatingthe integer multi of reciprocal vector G= a The values ofk for free e is not limited and the energy is continuous
for the case of 1D, the state function and energy for the empty lattice model should be: 2 2 (0) (0) 1 , 2 ik r k k k e E L m = = where 0 indicates the solution with no perturbation. The relation between energy and wave vector is parabolic. Considering the requirement of symmetry, it is splitted into many parts. The energy of any two equivalent points could be the same by translating the integer multi of reciprocal vector 2 Gh a = The values of k for free e is not limited and the energy is continuous
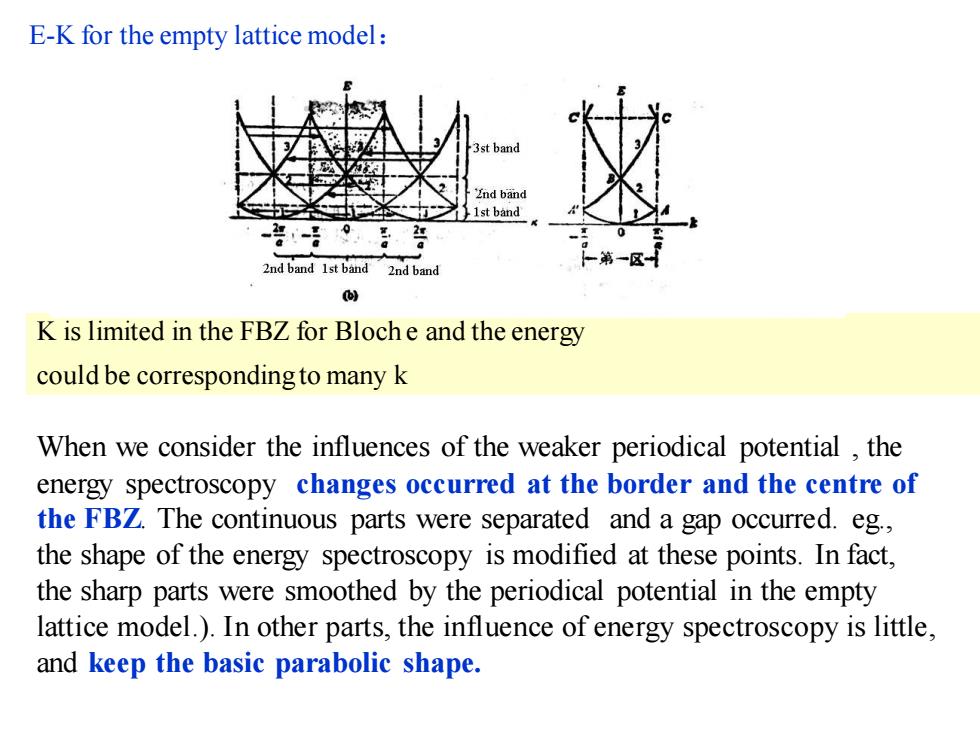
E-K for the empty lattice model: End band Ist band 24 2nd band Ist band 2nd band K is limited in the FBZ for Bloche and the energy could be corresponding to many k When we consider the influences of the weaker periodical potential,the energy spectroscopy changes occurred at the border and the centre of the FBZ.The continuous parts were separated and a gap occurred.eg., the shape of the energy spectroscopy is modified at these points.In fact, the sharp parts were smoothed by the periodical potential in the empty lattice model.).In other parts,the influence of energy spectroscopy is little, and keep the basic parabolic shape
E-K for the empty lattice model: K is limited in the FBZ for Bloch e and the energy could be corresponding to many k When we consider the influences of the weaker periodical potential , the energy spectroscopy changes occurred at the border and the centre of the FBZ. The continuous parts were separated and a gap occurred. eg., the shape of the energy spectroscopy is modified at these points. In fact, the sharp parts were smoothed by the periodical potential in the empty lattice model.). In other parts, the influence of energy spectroscopy is little, and keep the basic parabolic shape
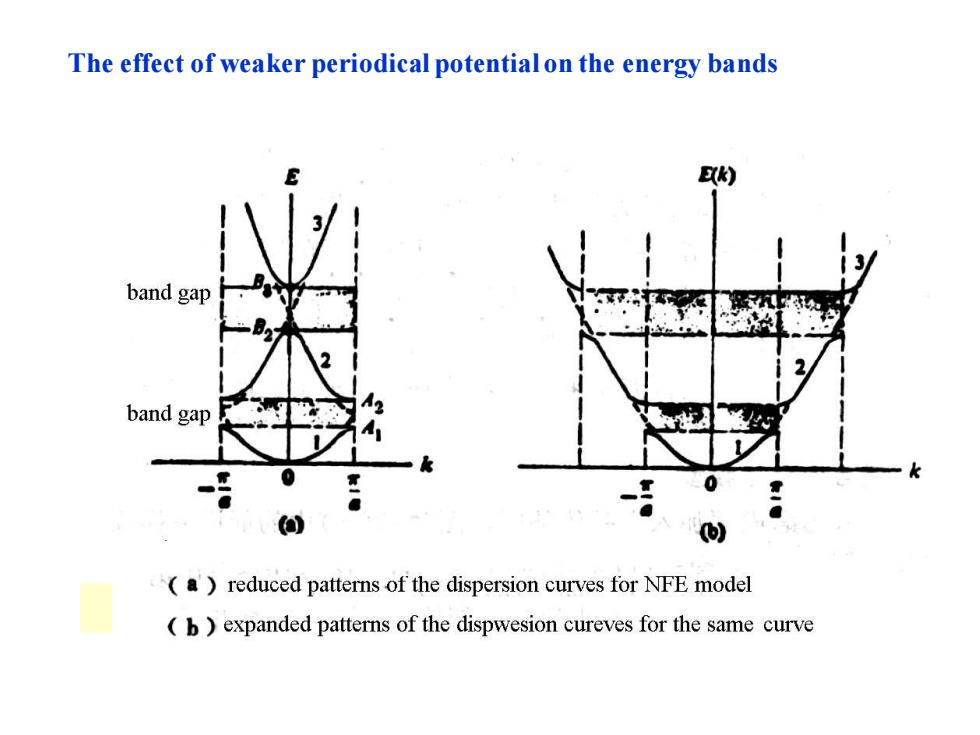
The effect of weaker periodical potential on the energy bands band gap band gap (a)reduced patterns of the dispersion curves for NFE model b expanded patterns of the dispwesion cureves for the same curve
The effect of weaker periodical potential on the energy bands
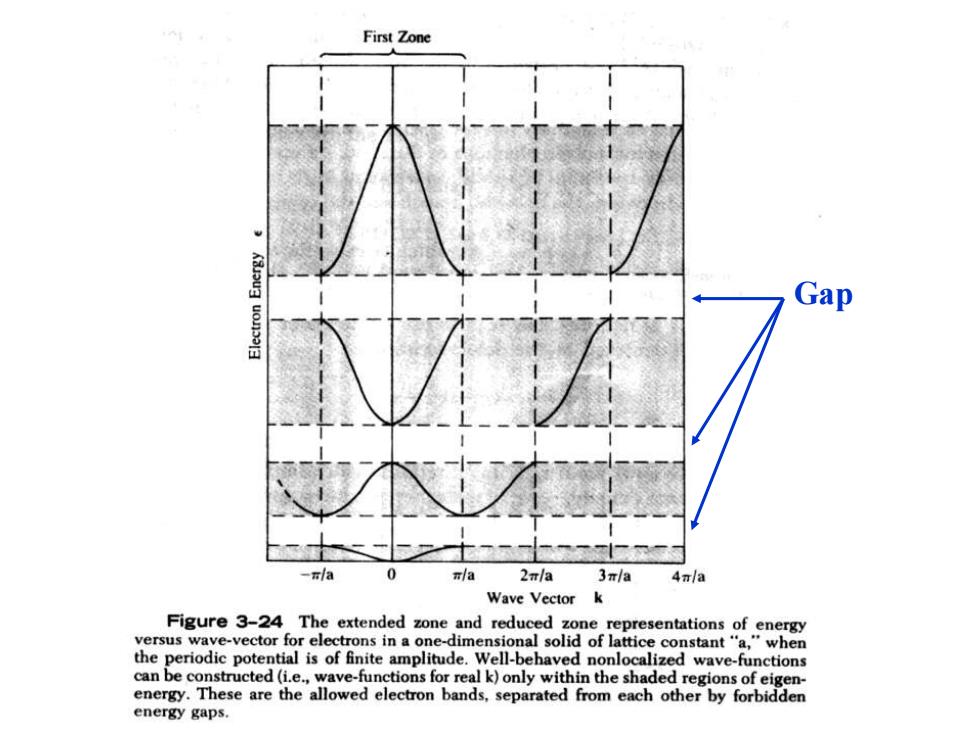
First Zone Gap -/a la2πla3πla4/a Wave Vector k Figure 3-24 The extended zone and reduced zone representations of energy versus wave-vector for electrons in a one-dimensional solid of lattice constant"a,"when the periodic potential is of finite amplitude.Well-behaved nonlocalized wave-functions can be constructed(i.e.,wave-functions for real k)only within the shaded regions of eigen- energy.These are the allowed electron bands,separated from each other by forbidden energy gaps
Gap