
5.5 The symmetry of bands The symmetry of crystal leads to the symmetry of electron motion.So,the eigenenergy and states also possess symmetry which describe the electron motion status.The understanding of the symmetry is favorable to the simplification of problems.For example,when we are calculating or draw the diagram of bands in the k space,we can fully exploit the band symmetry
5.5 The symmetry of bands The symmetry of crystal leads to the symmetry of electron motion. So, the eigenenergy and states also possess symmetry which describe the electron motion status. The understanding of the symmetry is favorable to the simplification of problems. For example, when we are calculating or draw the diagram of bands in the k space, we can fully exploit the band symmetry

The symmetry of E(k)function 5.5.1 E(k)=E(k+Gp) Translation symmetry If reduced wave vector k is changed by a reciprocal vector,the phase change indeed is the same,eg,k is equal to k+GSo,we can regard that E(k)is the periodic function in the k space,whose periodicity is the reciprocal vector.The values scope of the k is the Wigner-Seitz cell in the reciprocal lattice space,eg,the FBZ Based on the translation symmetry,we can translate the parts of the second Brillouin zone into the FBZ by a reciprocal vector. Similarly,More terms of Brillouin zone can also be superposed with the FBZ by the appropriate translation.Noteworthily,the above expression could only be correct in the same band
If reduced wave vector k is changed by a reciprocal vector, the phase change indeed is the same, eg, k is equal to k+Gh . So, we can regard that En (k) is the periodic function in the k space, whose periodicity is the reciprocal vector. The values scope of the k is the Wigner-Seitz cell in the reciprocal lattice space, eg, the FBZ. Based on the translation symmetry, we can translate the parts of the second Brillouin zone into the FBZ by a reciprocal vector. Similarly, More terms of Brillouin zone can also be superposed with the FBZ by the appropriate translation. Noteworthily, the above expression could only be correct in the same band. The symmetry of En (k) function ( ) ( ) n n Gh E k E k 5.5.1 = + Translation symmetry
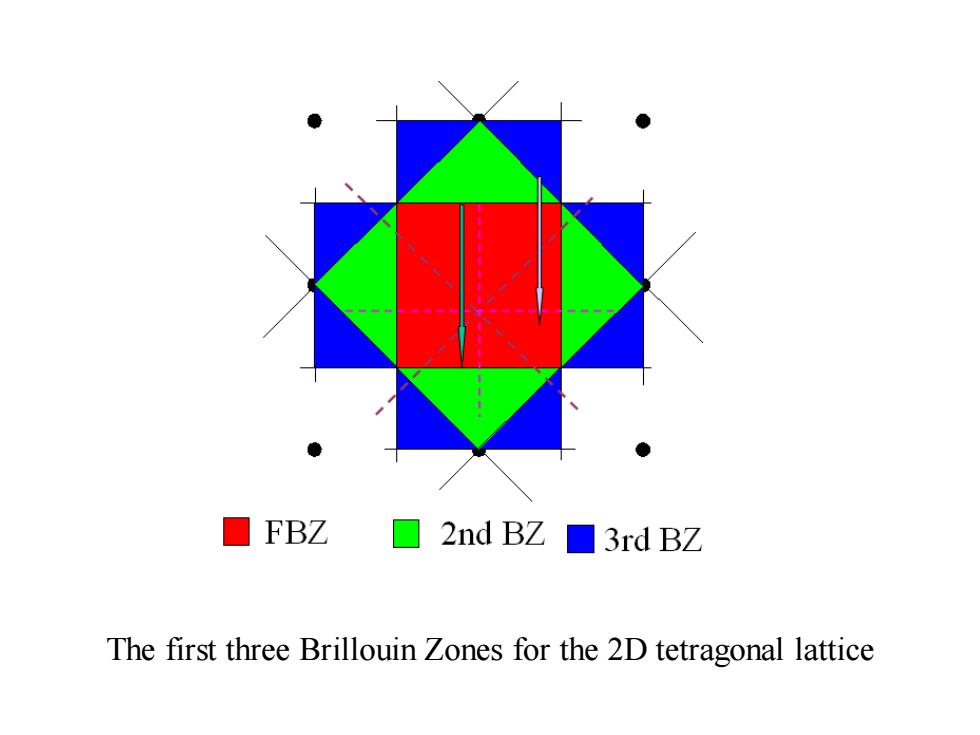
☐FBZ □ 2ndBZ■3rdBZ The first three Brillouin Zones for the 2D tetragonal lattice
The first three Brillouin Zones for the 2D tetragonal lattice

FBZ 2nd BZ 3rd BZ 4th BZ Simple Cubic Lattice,FBZ; 2nd BZ:3rd BZ:4th BZ
Simple Cubic Lattice, FBZ; 2nd BZ; 3rd BZ; 4th BZ FBZ 2nd BZ 3rd BZ 4th BZ

5.5.2 En(k)=En(ak) Point group symmetry the bands have the same symmetry with the lattice,where a is an any point symmetry operator Based on the Schrodinger equation HVn()=E,(kwnk() For the fact that the point group of crystal is kept unchanged after the point operator,so after the operation of a,the wavefunction is changed as (F)=Wnk(ar) Which should be a eigenfunction with the same eigenvalue V(+aR)=eark(cF The dot product is supposed to be the same after the point operation
E (k ) E ( k ) n n = the bands have the same symmetry with the lattice, where is an any point symmetry operator 5.5.2 Point group symmetry ( ) ( ) ( ) ˆ H r E k r nk n nk = Based on the Schrodinger equation Which should be a eigenfunction with the same eigenvalue For the fact that the point group of crystal is kept unchanged after the point operator, so after the operation of , the wavefunction is changed as (r) ( r) n nk = ( r R ) e ( r) nk ik R nk n n + = The dot product is supposed to be the same after the point operation