
6.4 The electron motion in a constant electric field Take the 1D tight-binding approximation as an example E'(k)=E;-Jo-2J coska s is the atomic energy level.SetJ>0,thus,k=0 is the band bottom;k=±π/a is the band top. ()=I ds2asinka h2 h2 ,m*= h dk h d2E dk2 2a2J coska At k=0 and k=tn/a,the velocity of electron is v(k)=0;but at k=+n/2a,v(k)is maximum or minimum values,respectively
Take the 1D tight-binding approximation as an example ( ) 0 1 2 cos i E k J J ka i = − − I is the atomic energy level. Set J1 >0, thus, k=0 is the band bottom; k=/a is the band top. ( ) 1 1 d 2 sin d E aJ v k ka k = = 2 2 2 1 2 2 d d 2 cos E k m a J ka = = At k = 0 and k= /a, the velocity of electron is v(k)=0; but at k= /2a, v(k) is maximum or minimum values, respectively. 6.4 The electron motion in a constant electric field

E(k) m (k) -h-2a -元归 a 0 2a xa -元da 0 π/a Clearly,at the top and bottom of energy band,the velocity is zero. There are maximum and minimum value between them.at the bottom:m*>0,at top:m*<0,in the middle:m*co. We will discuss the movement of electrons in constant electric field starting based on the images
Clearly, at the top and bottom of energy band, the velocity is zero. There are maximum and minimum value between them. at the bottom: m*>0,at top: m*<0, in the middle: m*→±∞. We will discuss the movement of electrons in constant electric field starting based on the images

a)The motion vision in the k space Apply a constant electric field along the -x direction,the force on the electrons equals:Fe along the +x direction. k dk es There is F=h =eg we can obtained: =const dt dt h which means that the speed of electrons is a constant in the k space. In the quasi-classical motion,electrons travel in the same band. Therefore,the motion of electrons with constant velocity in k space means that the curve of energy eigenvalues of electrons are periodically changed as a function of E(k),that is,electrons are doing circular movement in k space,which can be understood from the Brillouin zone map in the next page
In the quasi-classical motion, electrons travel in the same band. Therefore,the motion of electrons with constant velocity in k space means that the curve of energy eigenvalues of electrons are periodically changed as a function of E(k), that is, electrons are doing circular movement in k space, which can be understood from the Brillouin zone map in the next page. a) The motion vision in the k space Apply a constant electric field along the –x direction, the force on the electrons equals: F=e along the +x direction. There is , we can obtained: which means that the speed of electrons is a constant in the k space. d d k F e t = = d const d k e t = =
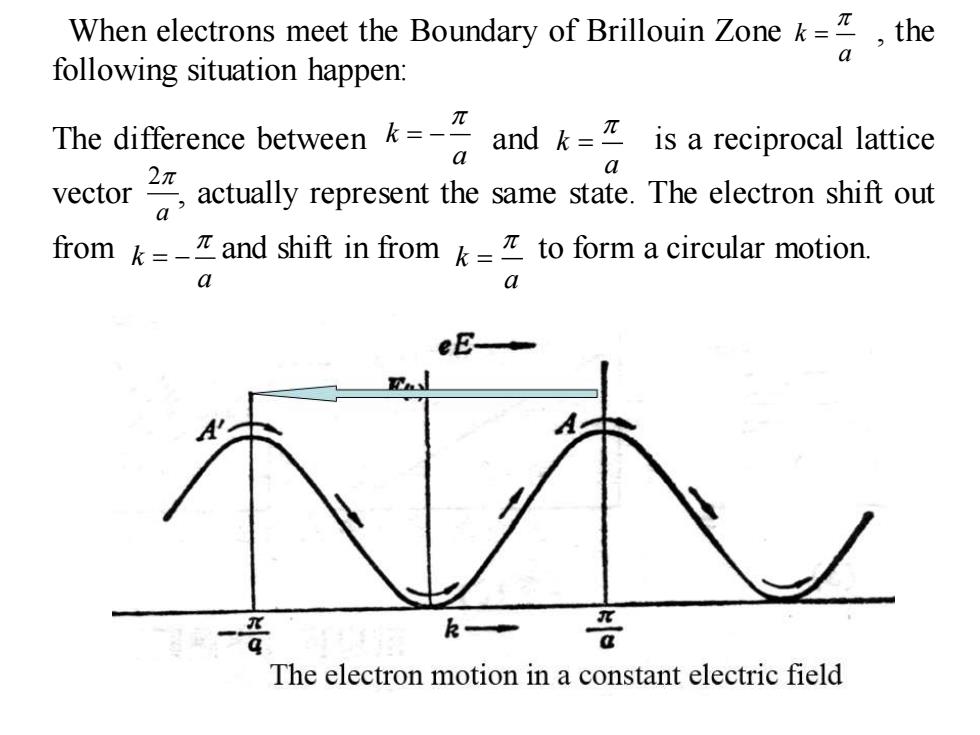
When electrons meet the Boundary of Brillouin Zone k=,the following situation happen: The difference betweenand reiprocal lattice oractually represent the same state.The electron shif from=and shift in from=to form a circular motion. eE k The electron motion in a constant electric field
When electrons meet the Boundary of Brillouin Zone , the following situation happen: The difference between and is a reciprocal lattice vector , actually represent the same state. The electron shift out from and shift in from to form a circular motion. k a = k a = k a = − k a k = a = − 2 a

when t=0,electron is located at the band bottom,k=0,m*>0. The velocity of electrons v can be accelerated by external force. When arrival at k=z/2a m*->o,v reach maximum.When k go over this point,m*<0,the velocity of electrons will be decelerated by external force,until k=-/2a the velocity decreased to be zero and electrons are at the top of band,m*<0.The velocity reversed and reach the maximum reverse speed at k=z/a When k exceeds this value,m*>0,so that the reverse speed decreases until k-0 and v-0.This is the speed of oscillation in a constant external field.(See above diagram
when t=0, electron is located at the band bottom, k=0, m*>0. The velocity of electrons v can be accelerated by external force. When arrival at , m*→∞, v reach maximum. When k go over this point, m*<0, the velocity of electrons will be decelerated by external force, until the velocity decreased to be zero and electrons are at the top of band, m*<0. The velocity reversed and reach the maximum reverse speed at . When k exceeds this value, m*>0, so that the reverse speed decreases until k=0 and v=0. This is the speed of oscillation in a constant external field. (See above diagram k a = 2 k a = k a = − 2