
4.5 Heat capacity of the lattice 6E Cy Dugong-Petit law,numerical value aT =3R independent of T Classical Statistical no numerical value at finite T Mechanics >k. For a vibrating atom: E=K+U .N =m+号mv2+m+号k,x2+k,y2+号k.z2 Classical statistical mechanics-equipartition theorem:in thermal equilibrium each quadratic term in the E has an average energy 5kg7,s0:E,=6kT)=3k7 Classically for a vibrator Cy
4.5 Heat capacity of the lattice Classical Statistical Mechanics Dugong-Petit law, numerical value independent of T no numerical value at finite T Classically for a vibrator 2 2 2 1 2 2 1 2 2 1 2 2 1 2 2 1 2 1 1 mv mv mv k x k y k z E K U = x + y + z + x + y + z m = + ky kx kz For a vibrating atom: Classical statistical mechanics — equipartition theorem: in thermal equilibrium each quadratic term in the E has an average energy , so: k T 2 B 1 E 6( kB T) 3kB T 2 1 1 = =
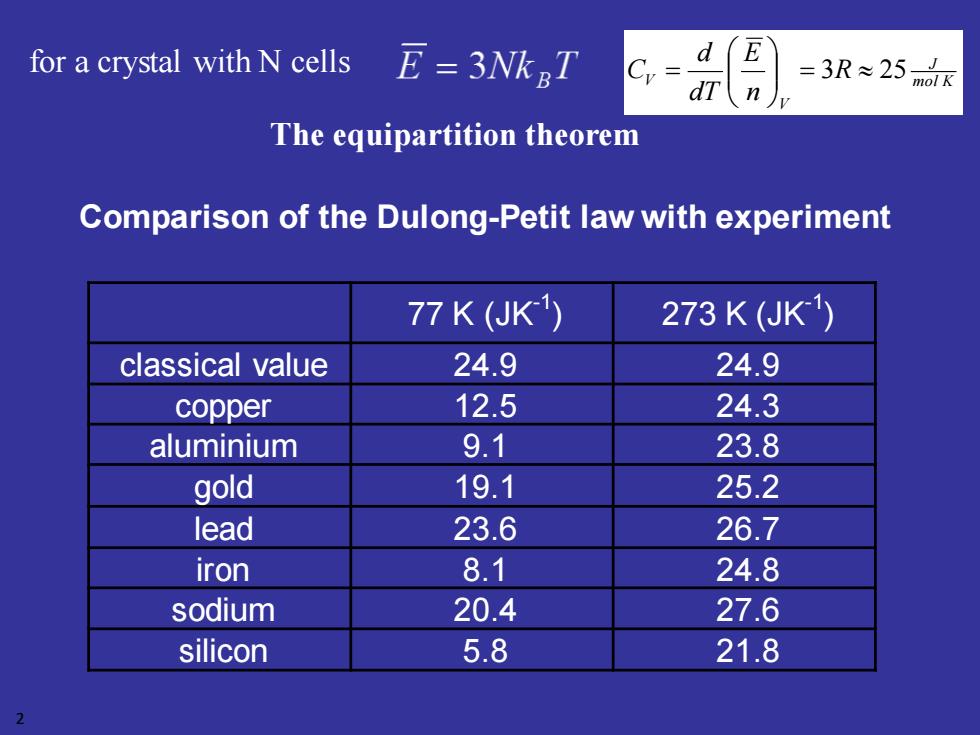
for a crystal with N cells E=3NkT d E =3R≈25 dT mol K n The equipartition theorem Comparison of the Dulong-Petit law with experiment 77K(UK1) 273K(JK1) classical value 24.9 24.9 copper 12.5 24.3 aluminium 9.1 23.8 gold 19.1 25.2 lead 23.6 26.7 iron 8.1 24.8 sodium 20.4 27.6 silicon 5.8 21.8 2
Comparison of the Dulong-Petit law with experiment 77 K (JK-1 ) 273 K (JK-1 ) classical value 24.9 24.9 copper 12.5 24.3 aluminium 9.1 23.8 gold 19.1 25.2 lead 23.6 26.7 iron 8.1 24.8 sodium 20.4 27.6 silicon 5.8 21.8 2 for a crystal with N cells The equipartition theorem mol K J V V R n E dT d C = 3 25 =

The vibration mode with frequency of is composed of subsystems 1 E,=(n,+ho, ThepmhabitoisuoyseanthegentmsaeorE-ah -n ho/kgT e P n ho/kgT P=e-eo)∑=-x Theavcrmgeprohabilit T'heaverngeenenyTor thivihrntionmoie E=∑PE ho e (eho,kar-1) the relation between lattice vibration frequency and temperature
The vibration mode with frequency of j is composed of subsystems The probability of subsystem in the quantum state of The average probability The average energy for this vibration mode / 1 ( ) 2 1 j B j E Tj j k T e = + − the relation between lattice vibration frequency and temperature / 2 / 2 ( ) ( 1) j B j B k T j V B k T B e C k k T e = −

oj/kgT C,=k, e o,k-1) (e kgT >>ho ha, =1+ hightemperature ho Cy= Cr≈kB Dugong-Petit law 00088 kgT<h0,ehok,≥>1 T→0 Cv→0 consistent with the experimental results
/ 2 / 2 ( ) ( 1) j B j B k T j V B k T B e C k k T e = − 2 2 2 (1 ) ( ) 1 [ ( ) ] 2 j j B V B B j j B B k T C k k T k T k T + + = + high temperature Dugong-Petit law 2 / 1 ( ) j B j V B k T B C k k T e = —— consistent with the experimental results low temperature

4.5.1 Einstein model ho e isuWehecrlcopeselofNatomsvibrnteswiththesnme freuenyog 3N E= ho Nha+ 3Nh@ Total energy )=2 ehab/kgT eha/kgT capacity Cy=( (e C,=3Nk/.K hoo/kgT e -Einstein heat e capacity function
3 ( ) 0 k T C Nk f B V B B = 4.5.1 Einstein model Assume the crystal composed of N atoms vibrates with the same frequency 0 / 1 ( ) 2 1 j B j E Tj j k T e = + − capacity Total energy / 2 / 0 0 2 ( 1) ( ) ( ) 0 0 − = k T k T B B B B B e e k T k T f -Einstein heat capacity function