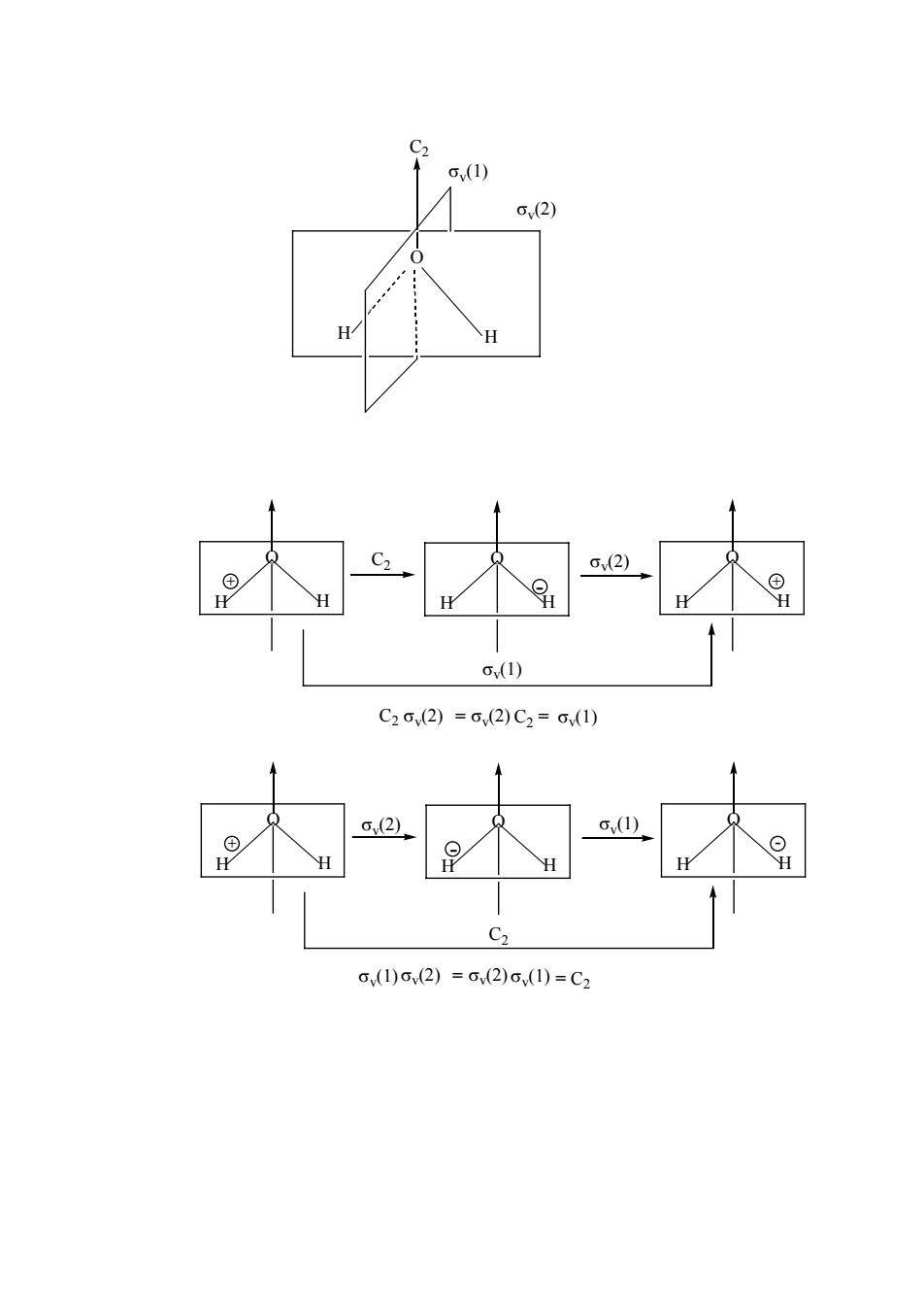
.2 G(1) C2,(2)=G2)C2=(1) C2 c(1)(2)=(2)c(1)=C2
O H H C2 σv(1) σv(2) - O H H C2 + O H H O H H σv(2) + σv(1) O H H C2 + O H H - O H H σv(2) σv(1) - C2 σv(2) σv = = (2) C2 σv(1) C2 σv(2) σv σv(1) = (2) σv(1) =
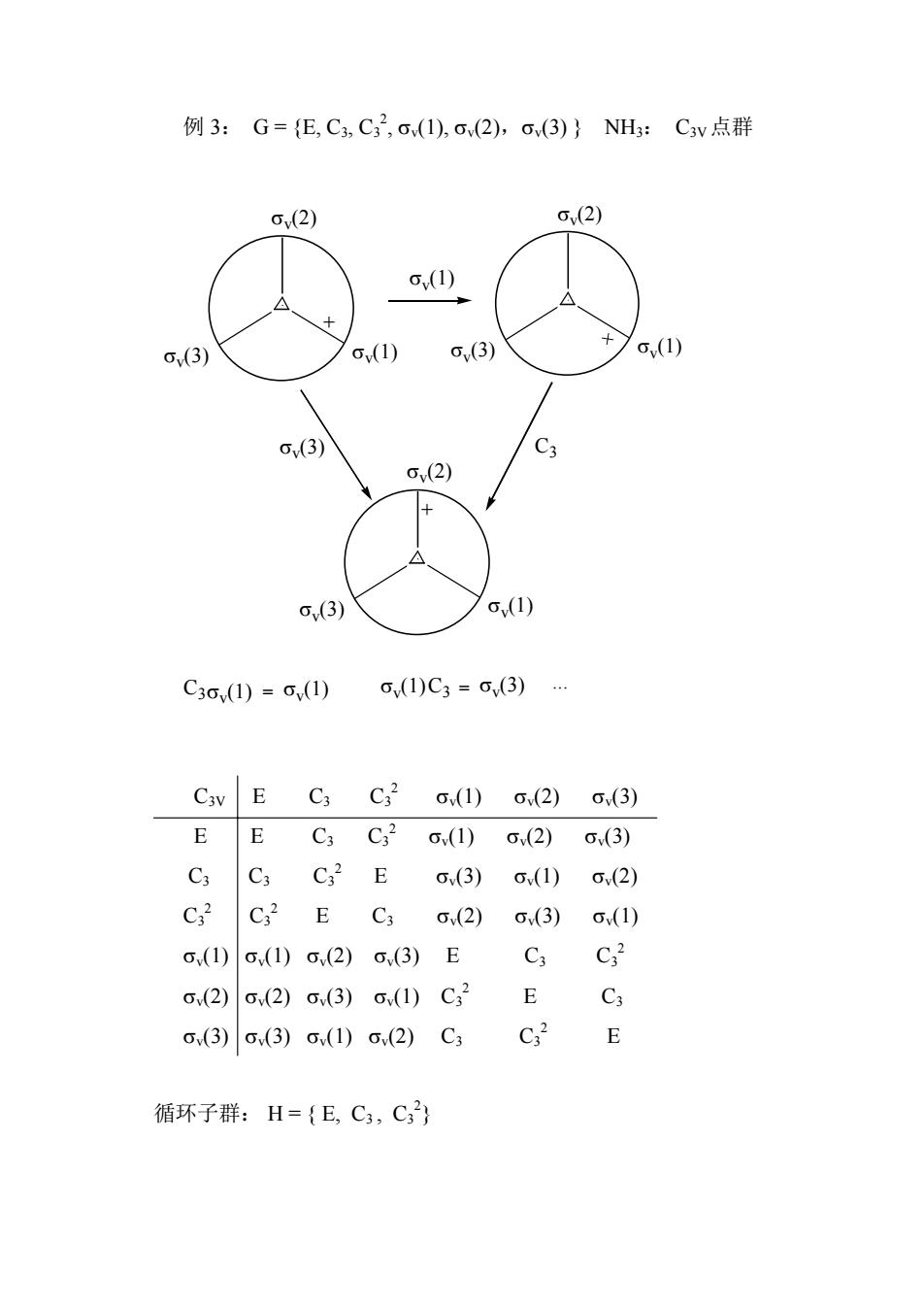
例3:G={E,C,C32,o(1),o(2),G(3)}NH3:C3v点群 0(2) 2) σ(1) o(3) o(1) c(3) o(1) (3) o(2) (3) C361)=o(1) o(1)C3=(3)… Cav E C3 C (1)G(2)G(3) EEC3C,2o(1)c2)o(3) CC3C2Eo.(3)G(1)o(2) C C2 E C3 (2)(3)(10) ()o,().2)(3)ECC2 o(2)o,(2)0(3)6(1)C32EC3 o(3)σ(3)(6.2)C3C2E 循环子群:H={E,C,C)
例 3: G = {E, C3, C3 2 , σv(1), σv(2),σv(3) } NH3: C3V点群 σv(1) σv(2) σv(3) + σv(1) σv(2) σv(3) σv(1) σv(1) σv(2) σv(3) + σv C3 (3) σv C3 (1) = σv(1) σv(1)C3 = σv(3) ... C3V E C3 C3 2 σv(1) σv(2) σv(3) E E C3 C3 2 σv(1) σv(2) σv(3) C3 C3 C3 2 E σv(3) σv(1) σv(2) C3 2 C3 2 E C3 σv(2) σv(3) σv(1) σv(1) σv(1) σv(2) σv(3) E C3 C3 2 σv(2) σv(2) σv(3) σv(1) C3 2 E C3 σv(3) σv(3) σv(1) σv(2) C3 C3 2 E 循环子群: H = { E, C3 , C3 2 }
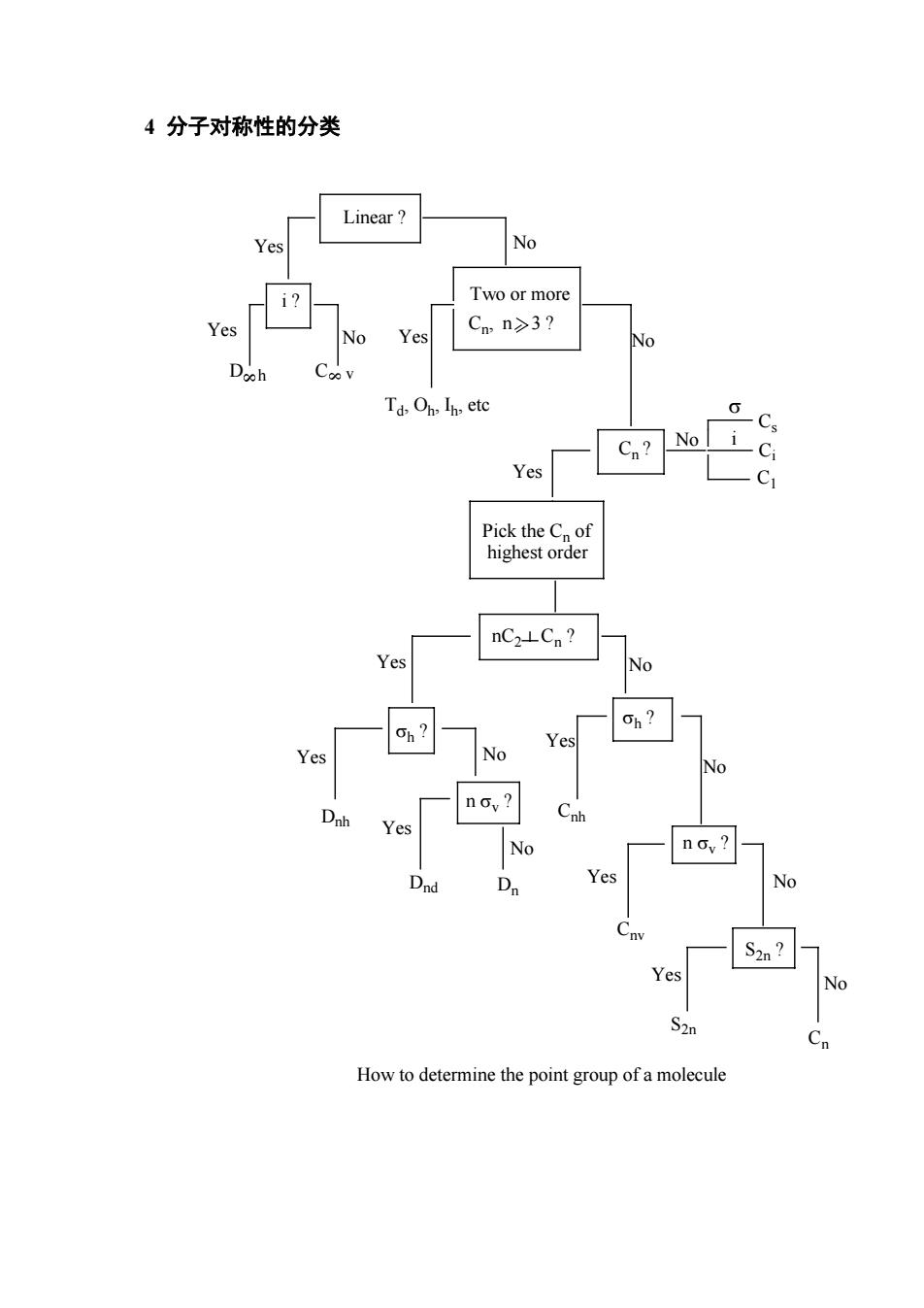
4分子对称性的分类 Linear? Yes i? Two or more Ye Td.Oh-Ih etc Yes ca nC2-Cn? Yes Ch? Ch? Yes No n Gy? Yes No Dnd Dn Yes How to determine the point group of a molecule
4 分子对称性的分类 Linear ? i ? No Two or more Cn, n 3 ? Yes No Yes D h C v Td, Oh, Ih, etc Yes No Cn ? Cs Ci C1 No σ i Pick the Cn of highest order nC2 Cn ? Yes Yes No σh ? n σv ? σh ? Yes No Dnh Yes No Dnd Dn Yes Cnh n σv ? No Yes No Cnv S2n ? Yes No S2n Cn How to determine the point group of a molecule
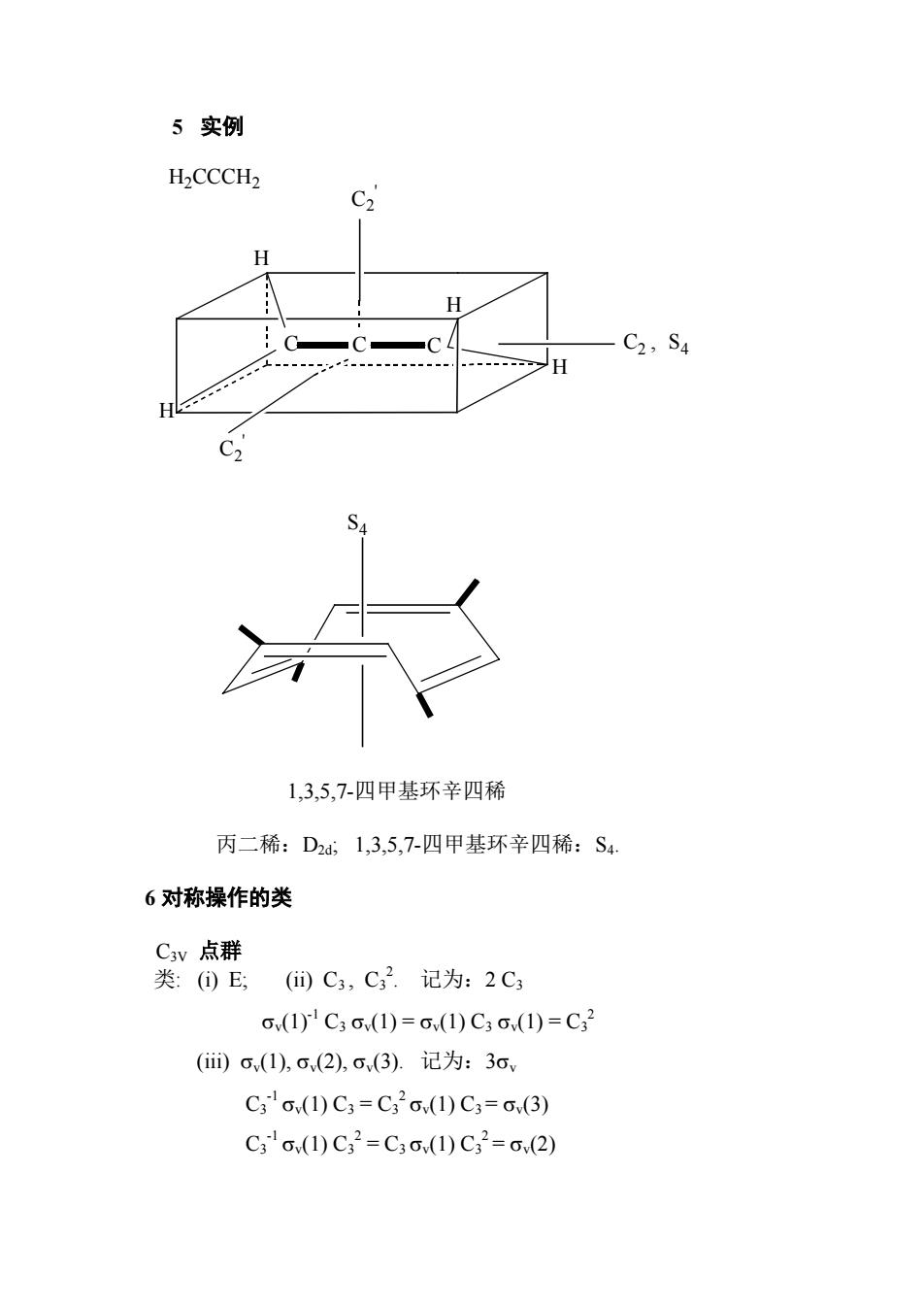
5实例 H>CCCH2 C,1 C2,S4 ..H 1,3,5,7-四甲基环辛四稀 丙二稀:D2d,1,3,5,7-四甲基环辛四稀:S4 6对称操作的类 C3v点群 类:(①E,(C,C2.记为:2C (1)'C3o(1)=o(1)C3o(1)=C2 (ii)o,(1),o(2),o(3).记为:3o C3o(1)C3=C32o(1)C3=o,(3) C3o1)C32=C3o1)C32=o(2)
5 实例 C C C H H H H C2 ' C2 ' C2 , S4 H2CCCH2 S4 1,3,5,7-四甲基环辛四稀 丙二稀:D2d; 1,3,5,7-四甲基环辛四稀:S4. 6 对称操作的类 C3V 点群 类: (i) E; (ii) C3 , C3 2 . 记为:2 C3 σv(1)-1 C3 σv(1) = σv(1) C3 σv(1) = C3 2 (iii) σv(1), σv(2), σv(3). 记为:3σv C3 -1 σv(1) C3 = C3 2 σv(1) C3 = σv(3) C3 -1 σv(1) C3 2 = C3 σv(1) C3 2 = σv(2)