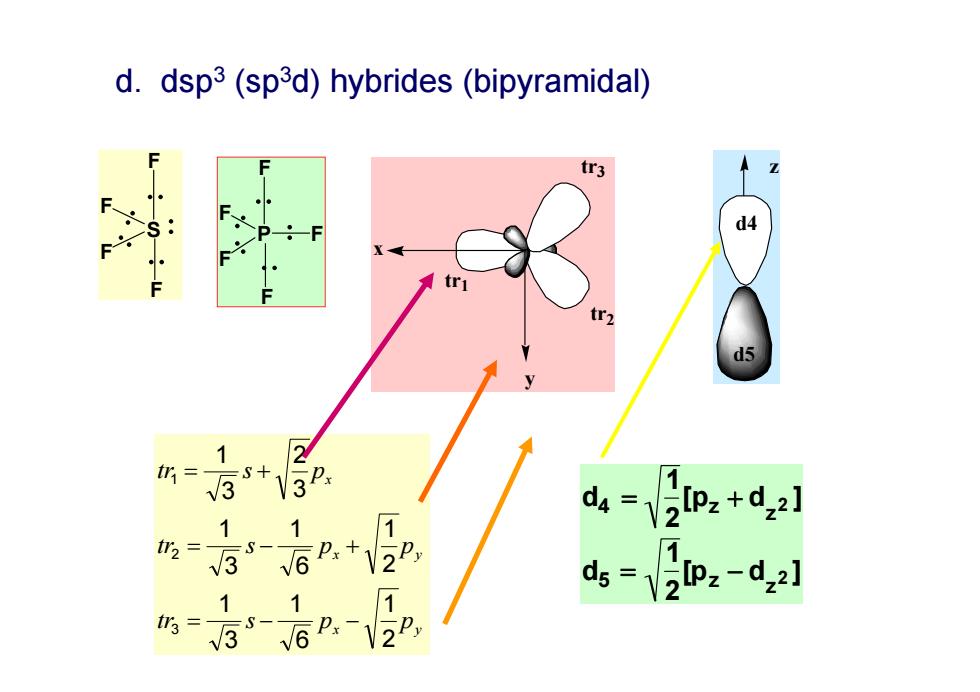
d.dsp3(sp3d)hybrides(bipyramidal) d4 所s1 3+3P. 1.1 1 4=2lp:+d2l S一 3 Px+ √6 ds-yz:-dz:] 1 3-6P.-12P
P F F F F F x y x y x tr s p p tr s p p tr s p 2 1 6 1 3 1 2 1 6 1 3 1 3 2 3 1 3 2 1 tr1 tr2 x y tr3 d4 12[pz dz2 ] d5 12[pz dz2 ] d4 d5 z S F F F F d. dsp3 (sp3d) hybrides (bipyramidal)
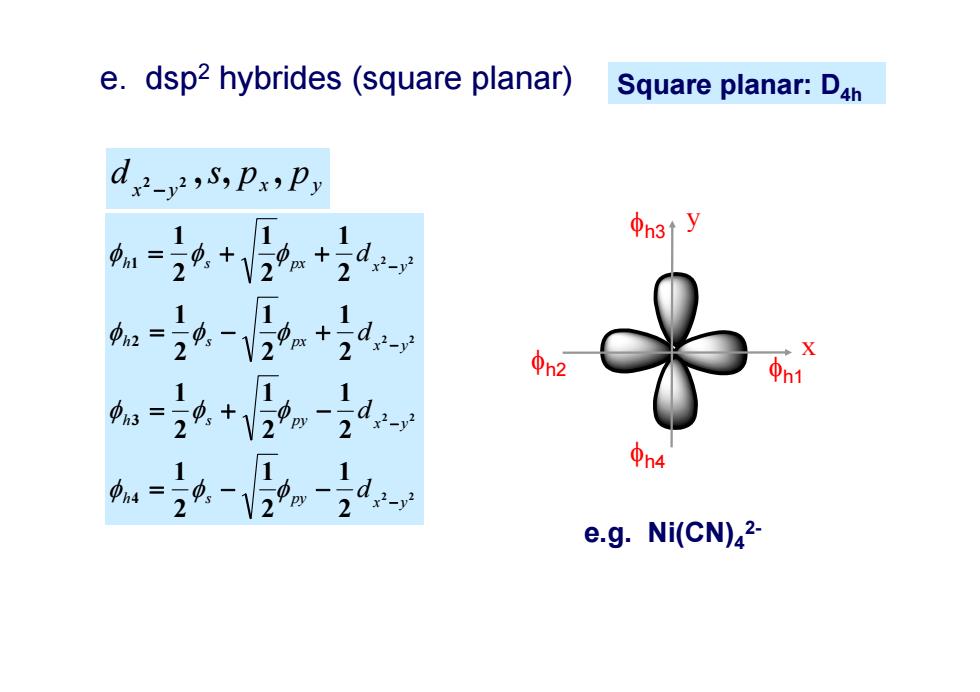
e.dsp2 hybrides (square planar) Square planar:D4h de,5,Px,Py φh3ty 1= 21 d- d2-y φ3 ①4 e.g.Ni(CN)2-
Square planar: D4h 2 2 2 2 2 2 2 2 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 4 3 2 1 py x y h s py x y h s px x y h s px x y h s d d d d x y x y d 2 2 ,s, p , p h1 x y h3 h2 h4 e.g. Ni(CN)42- e. dsp2 hybrides (square planar)
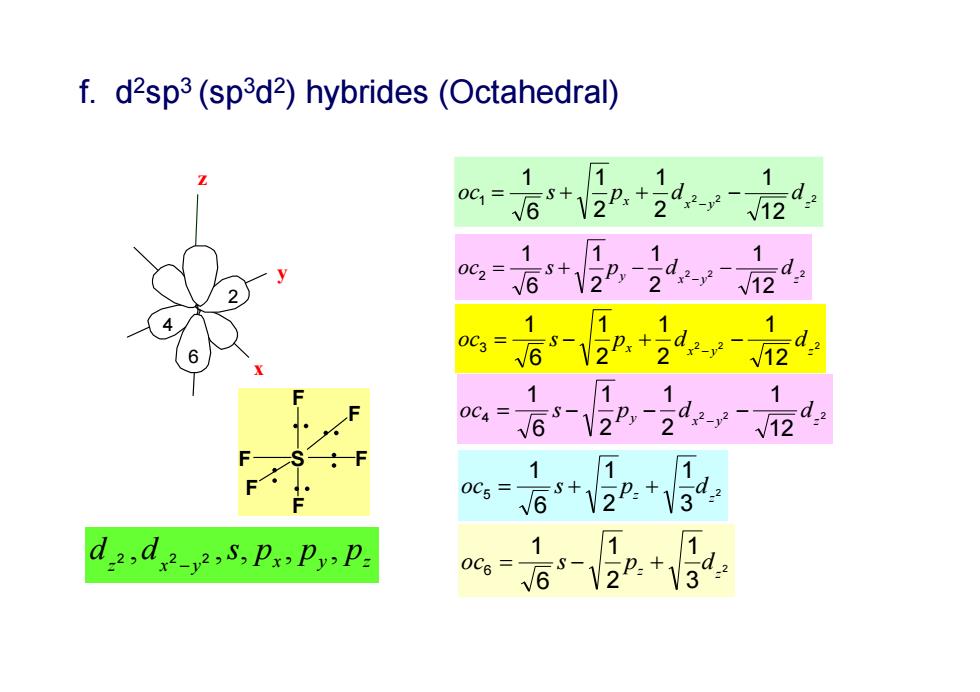
f.d2sp3(sp3d2)hybrides(Octahedral) 1 1 1 oc,=6s+22:+ d,2-y-12 1 1 +2P,2129 =S 1 , 1 0C3= -V2+ d2-y2- √12 1 1 1 0C4= 69-2,242 √12 1 1 0C5= +2P.+3 dad5,PxPy.P: 1 1 0c6= s-V2P:+V39
5 1 2 3 4 6 x y z 2 3 1 2 1 6 1 5 z z oc s p d 2 2 2 12 1 2 1 2 1 6 1 1 x y z x oc s p d d 2 2 2 12 1 2 1 2 1 6 1 2 x y z oc s py d d 2 2 2 12 1 2 1 2 1 6 1 3 x y z oc s px d d 2 2 2 12 1 2 1 2 1 6 1 4 x y z oc s py d d 2 3 1 2 1 6 1 6 z z x y x y z oc s pz d d 2 ,d 2 2 ,s, p , p , p f. d2sp3 (sp3d2) hybrides (Octahedral) F S F F F F F

Hybridization schemes spndm gives a“complete'”set of hybrid orbitals for“any'geometry. sp linear sp2 trigonal planar sp3 tetrahedral sp3d (d,2) trigonal bipyramidal sp3d(dx2-y2) square-based pyramidal sp3d2 octahedral sp2d square planar
Hybridization schemes sp n d m gives a “complete” set of hybrid orbitals for “any” geometry. sp linear sp 2 trigonal planar sp 3 tetrahedral sp 3d (d z 2) trigonal bipyramidal sp 3d(d x 2 - y 2) square-based pyramidal sp 3 d 2 octahedral sp 2d square planar

3.The angle between two hybrid orbitals spn hybridation pn=Vap,+√1-Qφ2p pn=VC,p。+V1-02n ,=Va项.+V-a,p 中p=x,中x+y,02py+,中2p
3. The angle between two hybrid orbitals sp n hybridation h 2 s 2 p 1 p j h j j 2 s j 2 1 i hi i 2 s 1 i 2 p p i px i py i pz x y z i 2 2 where pi is