
随机事件 1.定义(p3定义1.1.2)试验中可能出现或可能不出现的情 况叫“随机事件”,简称"事件”记作A、B、C等 任何事件均可表示为样本空间的某个子集, 称事件A发生当且仅当试验的结果是子集A中的元素 2.两个特殊事件:必然事件S、不可能事件φ.(p3) 例如对于试验E,以下A、B、C即为三个随机事件: A=“至少出一个正面” =HHH,HHT,HTH,THH,HTT,THT,TTH; B=“两次出现同一面”={HHH,TTT} C=恰好出现一次正面”={HTT,THT,TTH} 再如,试验E6中D=“灯泡寿命超过1000小时” ={x:1000<x<T(小时)}
随机事件 1.定义 (p3定义1.1.2) 试验中可能出现或可能不出现的情 况叫“随机事件”, 简称“事件”.记作A、B、C等 任何事件均可表示为样本空间的某个子集. 称事件A发生当且仅当试验的结果是子集A中的元素 2.两个特殊事件: 必然事件S 、不可能事件.(p3) 例如 对于试验E2,以下A 、 B、C即为三个随机事件: A=“至少出一个正面” ={HHH, HHT, HTH, THH,HTT,THT,TTH}; B=“两次出现同一面”={HHH,TTT} C=“恰好出现一次正面”={HTT,THT,TTH} 再如,试验E6中D=“灯泡寿命超过1000小时” ={x:1000<x<T(小时)}

可见,可以用文字表示事件,也可以将事件表示为样本空 间的子集,后者反映了事件的实质,且更便于今后计算概 率 还应注意,同一样本空间中,不同的事件之间有一定的关 系,如试验邻,当试验的结果是HHH时,可以说事件A和B 同时发生了,但事件B和C在任何情况下均不可能同时发生 。易见,事件之间的关系是由他们所包含的样本点所决定 的,这种关系可以用集合之间的关系来描述。 三、事件之间的关系
三、事件之间的关系 可见,可以用文字表示事件,也可以将事件表示为样本空 间的子集,后者反映了事件的实质,且更便于今后计算概 率 还应注意,同一样本空间中,不同的事件之间有一定的关 系,如试验E2,当试验的结果是HHH时,可以说事件A和B 同时发生了;但事件B和C在任何情况下均不可能同时发生 。易见,事件之间的关系是由他们所包含的样本点所决定 的,这种关系可以用集合之间的关系来描述
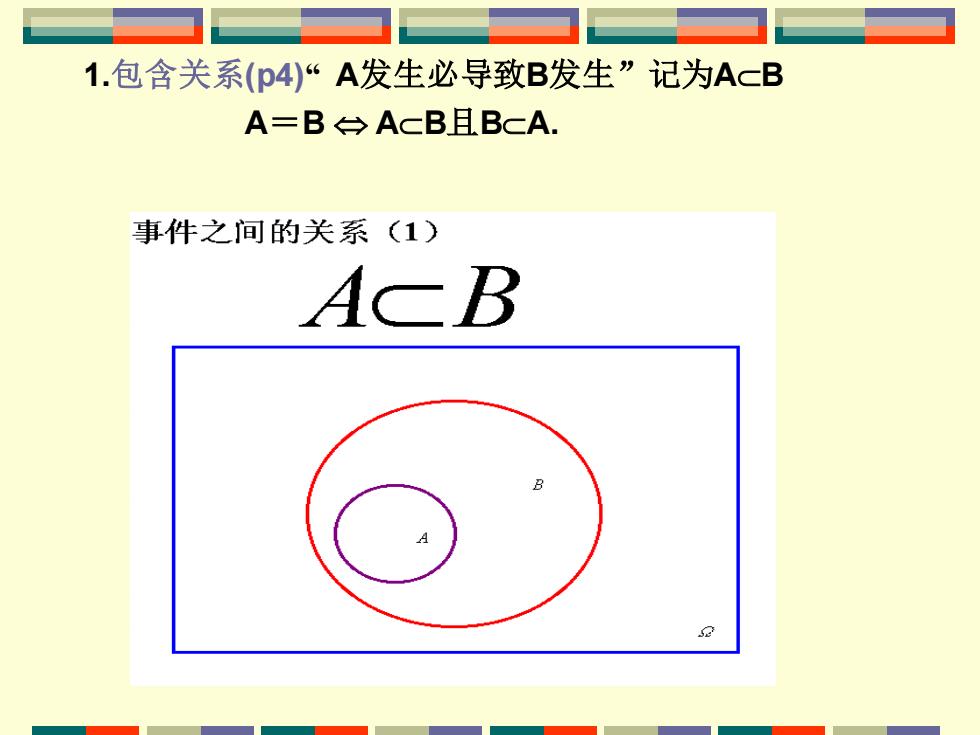
1.包含关系(p4)“A发生必导致B发生”记为AcB A=B台ACB且BCA. 事件之间的关系(1) ACB
1.包含关系(p4)“ A发生必导致B发生”记为AB A=B AB且BA
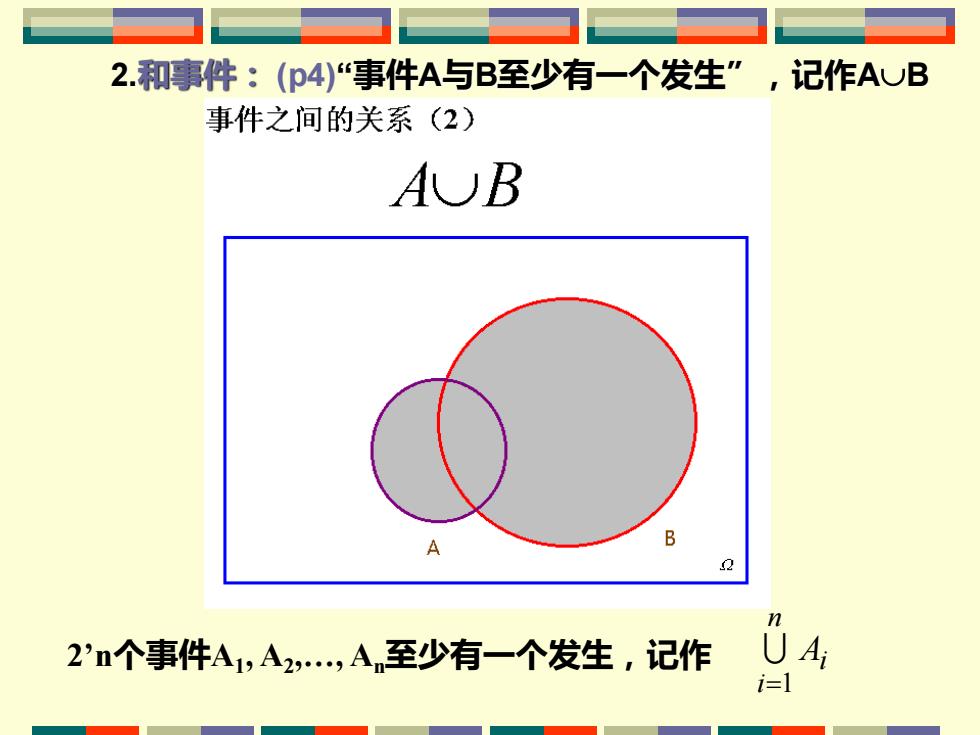
2.和事件:(p4)事件A与B至少有一个发生”,记作AUB 事件之间的关系(2) AUB B 2 n 2'n个事件A1,A2,A至少有一个发生,记作 i=l
2.和事件: (p4)“事件A与B至少有一个发生”,记作AB 2’n个事件A1 , A2 ,., An至少有一个发生,记作 i n i A =1
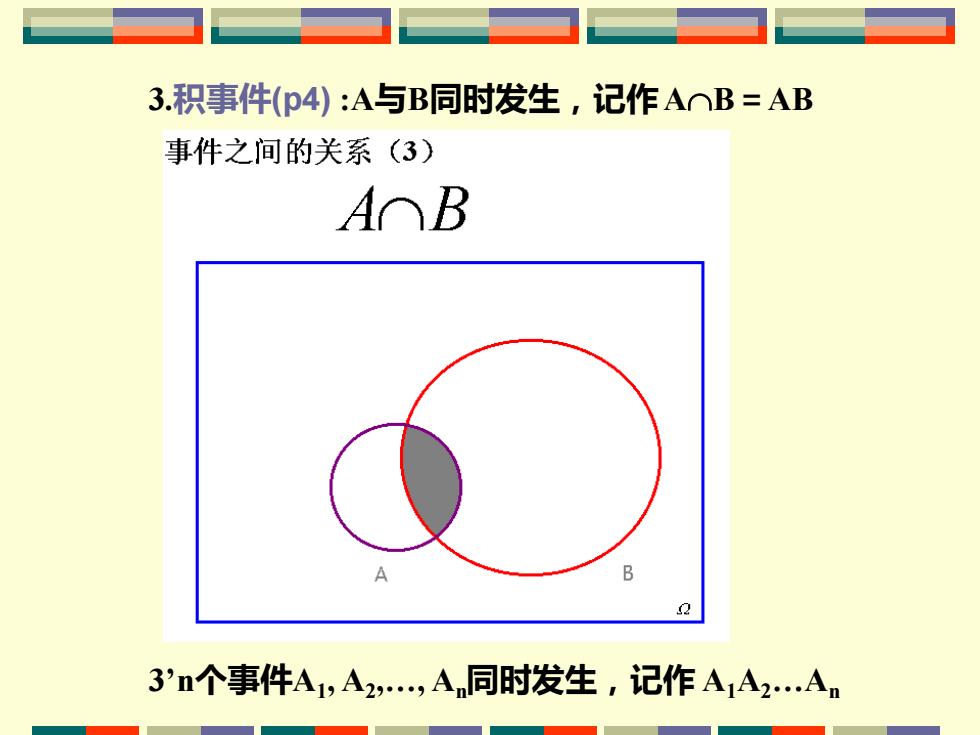
3.积事件(p4):A与B同时发生,记作A⌒B=AB 事件之间的关系(3) A⌒B B 2 3'n个事件A1,A2,A同时发生,记作A1A2An
3.积事件(p4) :A与B同时发生,记作AB=AB 3’n个事件A1 , A2 ,., An同时发生,记作 A1A2.An