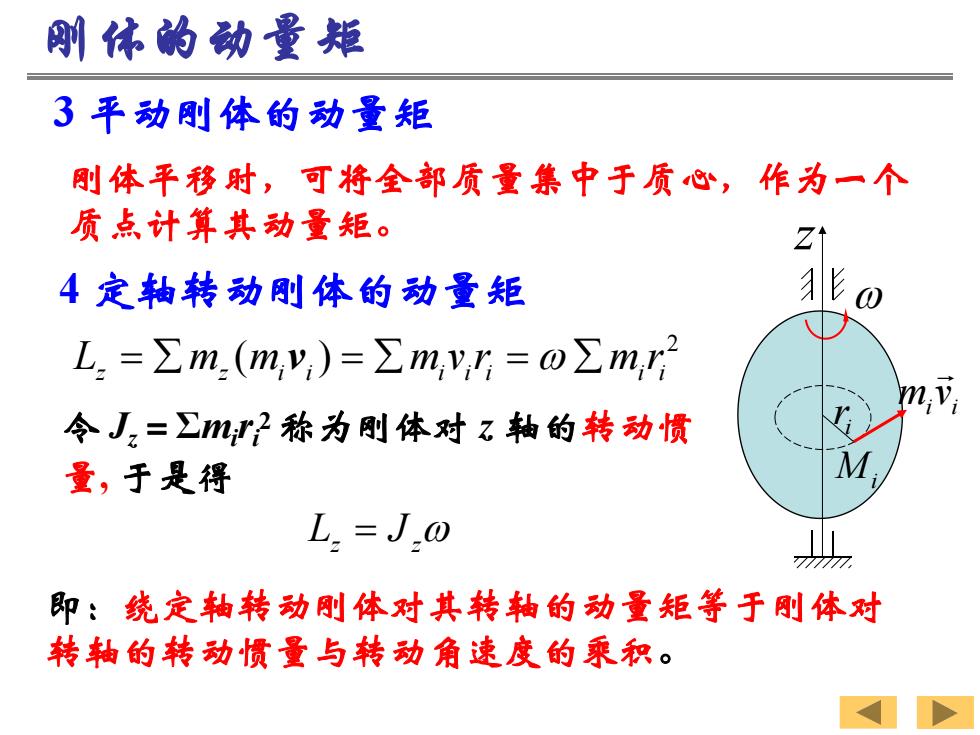
刚体的动量矩 了平动刚体的动量矩 则体平移时,可将全部质量集中于质心,作为一个 质点计算其动量矩。 Z1 4定轴转动则体的动量矩 L.=∑m(m,y)=∑m,y,=o∑m,r2 令J,=卫mH2称为则体对z轴的转动惯 量,于是得 L.=J.@ 即:绕定轴转动刚体对其转轴的动量矩等于刚体对 转轴的转动惯量与转动角速度的乘积
3 平动刚体的动量矩 刚体平移时,可将全部质量集中于质心,作为一个 质点计算其动量矩。 刚体的动量矩 4 定轴转动刚体的动量矩 2 ( ) L z mz mi i mi i i i i v v r m r 令 Jz=Σmiri 2 称为刚体对 z 轴的转动惯 量, 于是得 Lz J z 即:绕定轴转动刚体对其转轴的动量矩等于刚体对 转轴的转动惯量与转动角速度的乘积。 z Mi ir i i m v
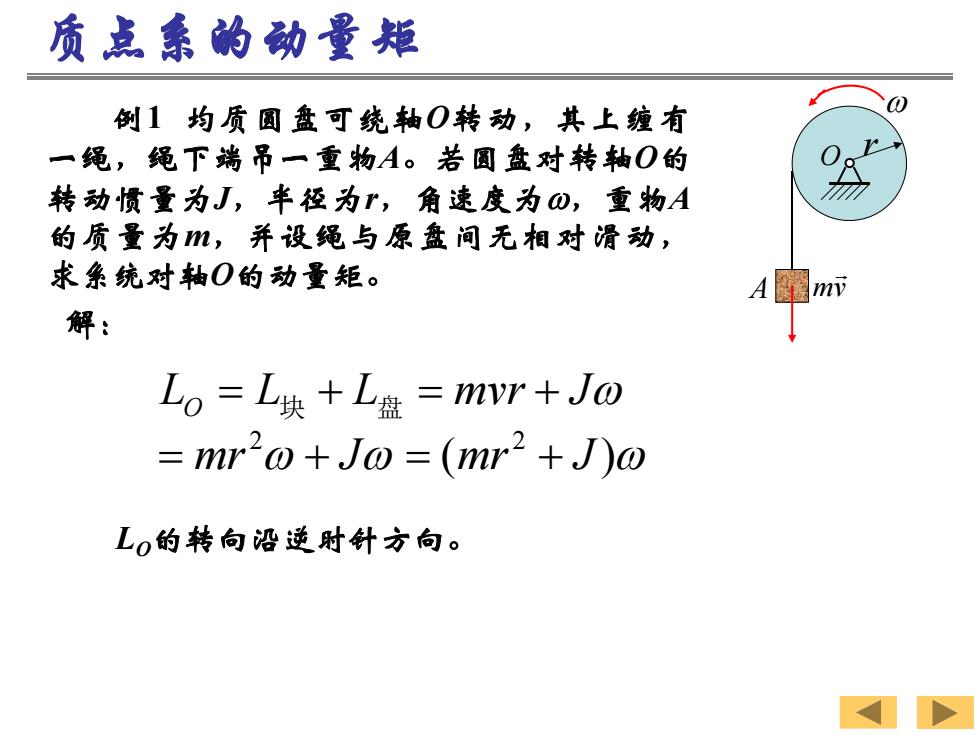
质点集的动量矩 例1均质圆盘可绕轴O转动,其上缠有 一绳,绳下端吊一重物A。若圆盘对转轴O的 转动惯量为J,半径为r,角速度为0,重物A 的质量为m,并设绳与原盘问无相对滑动, 求系统对轴O的动量矩。 解: Lo=L块+L盘=mr+J0 mr-@+Jo =(mr2+J)@ L0的转向沿逆时针方向
r O A mv 例1 均质圆盘可绕轴O转动,其上缠有 一绳,绳下端吊一重物A。若圆盘对转轴O的 转动惯量为J,半径为r,角速度为,重物A 的质量为m,并设绳与原盘间无相对滑动, 求系统对轴O的动量矩。 解: ( ) 2 2 mr J mr J L L L mvr J O 块 盘 LO的转向沿逆时针方向。 质点系的动量矩

11.2动量矩定理 11.2.1质点的动量矩定理 设质点对固定点0的动 量矩为Mo(w),作用力F对 Mo(mv) 同一点的矩为Mo(F可,如图 所示。 将动量矩对时间取一 Mo(F) 次导数,得 o(m)= d (r×mv) dt dr d ×mv+rx (mv) dt
11.2.1 质点的动量矩定理 设质点对固定点O的动 量矩为MO(mv),作用力F对 同一点的矩为MO(F) ,如图 所示。 d d ( ) ( ) d d d d ( ) d d O m m t t m m t t M v r v r v r v 11.2 动量矩定理 x y z O MO(mv) Q mv MO r (F) F 将动量矩对时间取一 次导数,得
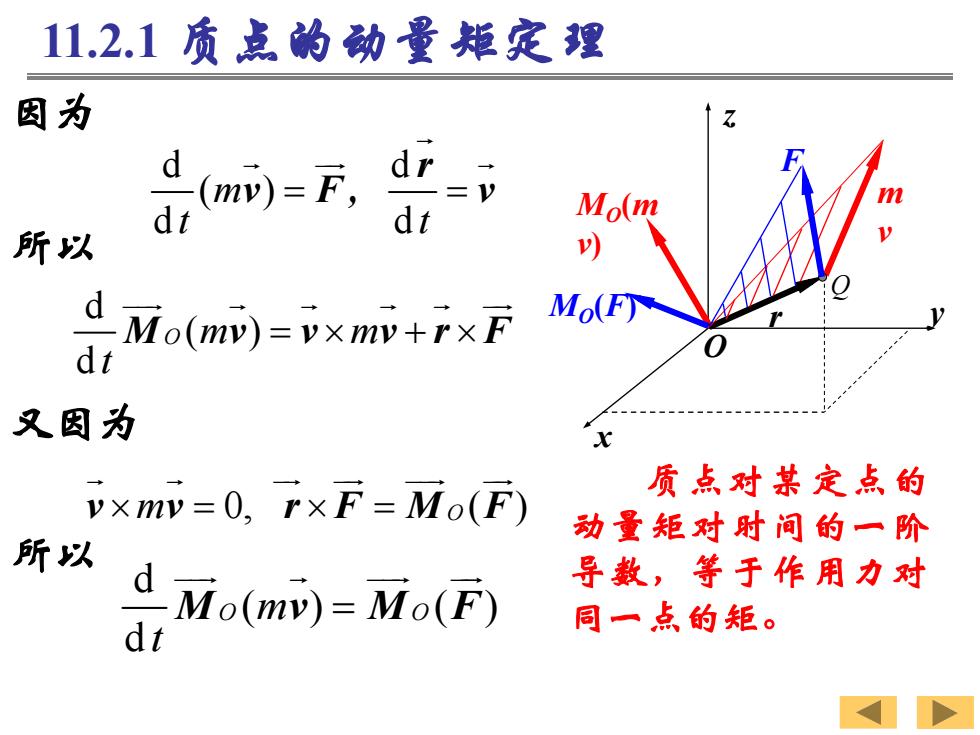
11.2.1质点的动量矩定理 因为 dmm=万,d=v dt Mo(m 所以 d Mo(mD)=vxmv+r×F Mo(F dt 又因为 v×mv=0,r×F=Mo(F) 质点对某定点的 动量矩对附间的一阶 所以 dio0mm=Mo( 导数,等于作用力对 dt 同一点的矩
m 0, O ( ) v v r F M F d ( ) ( ) d O m O t M v M F 11.2.1 质点的动量矩定理 d d ( ) d d m t t r v F , v d ( ) d O m m t M v v v r F 因为 所以 又因为 所以 x y z O MO(m v) Q m v MO r (F) F 质点对某定点的 动量矩对时间的一阶 导数,等于作用力对 同一点的矩
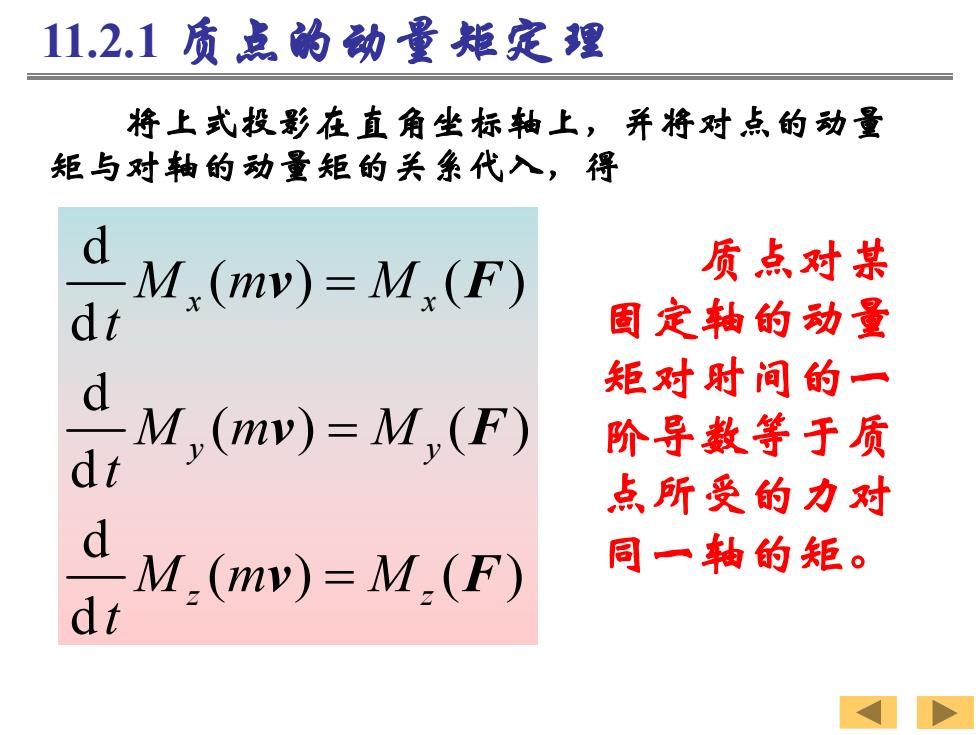
11.2.1质点的动量矩定理 将上式投影在直角坐标轴上,并将对点的动量 矩与对轴的动量矩的关系代入,得 d M.(mv)=M,(F) 质点对某 d t 固定轴的动量 d 矩对时间的一 M,(mv)=M,(F) 阶导数等于质 点所受的力对 d M.(mv)=M.(F) 同一轴的矩。 dt
将上式投影在直角坐标轴上,并将对点的动量 矩与对轴的动量矩的关系代入,得 d ( ) ( ) d d ( ) ( ) d d ( ) ( ) d x x y y z z M m M t M m M t M m M t v F v F v F 质点对某 固定轴的动量 矩对时间的一 阶导数等于质 点所受的力对 同一轴的矩。 11.2.1 质点的动量矩定理