
=a,,+b,中2x+C,02pmy For equivalent hybridization:the weighting of s orbital in each hybrid orbital is 1/3,and therefore a,=V1/3 中i=V1/34,+b,42m+C,中2py Supposed is parallel to the x-axis and is perpendicular to the y-axis 中n1=V1/30,+b,2m Normalization 中a1=V1/30,+V2/30 中1=V1/30+√21342x 中n=V1/30,+b,2x+C,py Normalization and orthogonality a,2+b2+c,2=1 2 1/3+b,2+c,2-1 a1a2+b,b2+cc2=0 1/3+√2/3b2+0c2=0 b2=-1/6 C2=±V1/2 h2 =V1/3。-1/642x+1/24p =V1/30,-V1/64m-V1/24m
hi i s i px i py a b c φ = φ + φ2 + φ2 For equivalent hybridization: the weighting of s orbital in each hybrid orbital is 1/3, and therefore = 1/ 3 i a Supposed φh1 is parallel to the x-axis and is perpendicular to the y-axis. h s px h s i px b 1 2 1 2 1/ 3 2 / 3 1/ 3 φ φ φ φ φ φ = + = + Normalization hi s i px i py b c 2 2 φ = 1/ 3φ + φ + φ hi s i px i py b c 2 2 φ = 1/ 3φ + φ + φ h1 s 3 2 px φ = 1/ 3φ + 2 / φ Normalization and orthogonality 1/ 3 2 / 3 0 0 1/ 3 1 2 2 2 2 2 2 + + ⋅ = + + = b c b c 0 1 1 2 1 2 1 2 2 2 2 2 2 2 + + = + + = a a b b c c a b c b2 = − 1/ 6 c2 = ± 1/ 2 h2 s 2 px 2 py φ = 1/ 3φ − 1/ 6φ + 1/ 2φ h3 s 2 px 2 py φ = 1/ 3φ − 1/ 6φ − 1/ 2φ
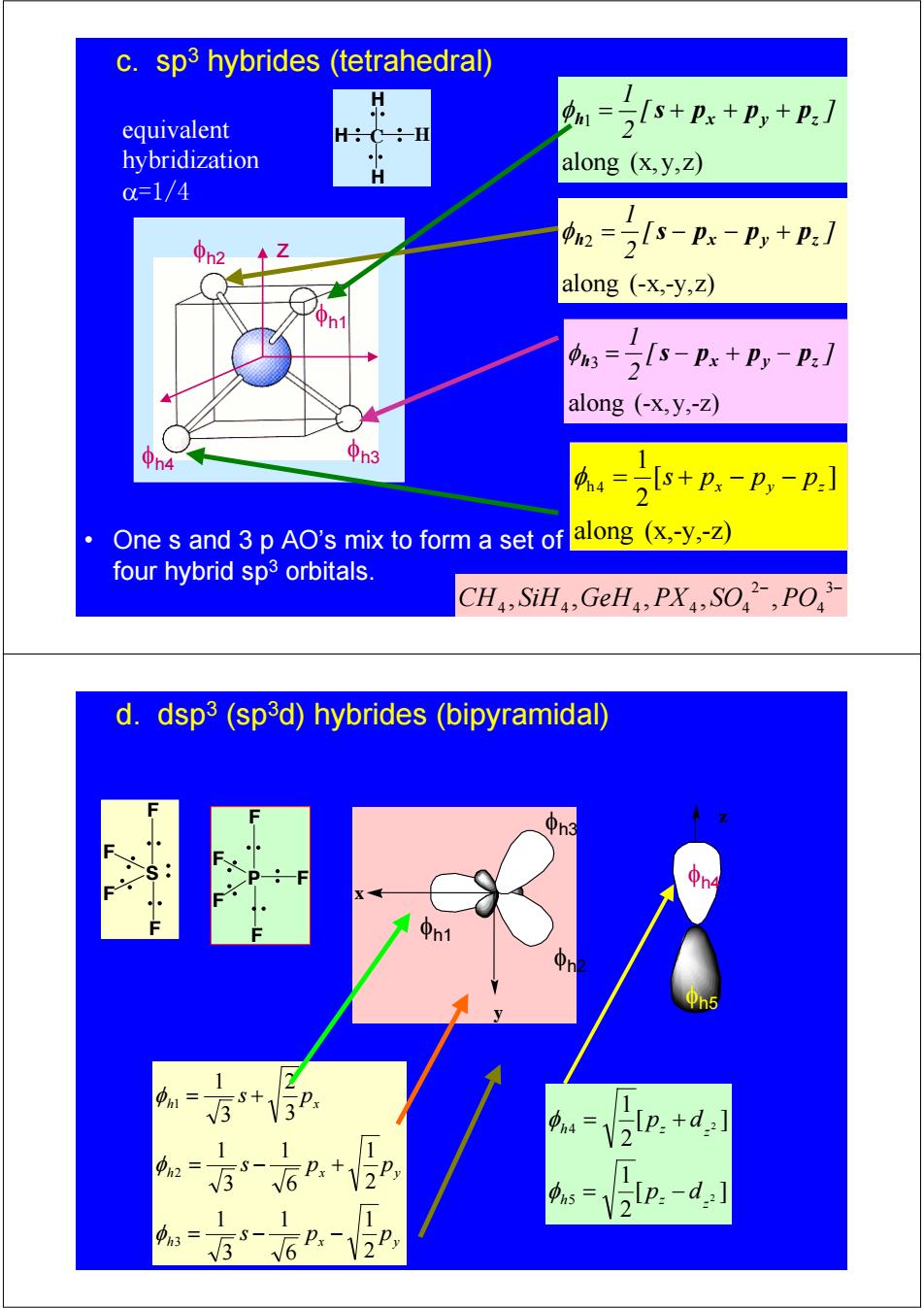
c.sp3 hybrides (tetrahedral) equivalent 1= 2+px+p,+P:] -H hybridization H along (x,y,z) c=1/4 2 22s-n-p,+:/ along (-x,-y,Z) 1 :=2s-Px+P,-P:] along (-x,y,-Z) h4 中n3 s+px -Py-p: 2 One s and 3 p AO's mix to form a set of along (x,-y,-Z) four hybrid sp3 orbitals. CH,SiH,GeHa,PX,SO,PO d.dsp3(sp3d)hybrides (bipyramidal) n3 1 m= 1 =V2Ip.+d:] 0h2= 12 Vlp:-d:] 1 1 S- 3 6 Px 2
H C H H H φh1 φh2 φh4 φh3 z along (-x,-y,z) 2 [ ] 2 1 h px py pz φ = s − − + along (x, y,z) 1 [ ] 2 1 h x y z φ = s + p + p + p along (x,-y,-z) [ ] 2 1 h 4 x y z φ = s + p − p − p along (-x,y,-z) 3 [ ] 2 1 h px py pz φ = s − + − • One s and 3 p AO’s mix to form a set of four hybrid sp3 orbitals. equivalent hybridization α=1/4 c. sp3 hybrides (tetrahedral) − 3− 4 2 4 4 4 4 4 CH , SiH ,GeH , PX , SO , PO P F F F F F h x y h x y h x s p p s p p s p 2 1 6 1 3 1 2 1 6 1 3 1 3 2 3 1 3 2 1 = − − = − + = + φ φ φ φh1 φh2 x y φh3 [ ] 2 1 [ ] 2 1 2 2 5 4 z h z z h z p d p d = − = + φ φ φh4 φh5 z S F F F F d. dsp3 (sp3d) hybrides (bipyramidal)
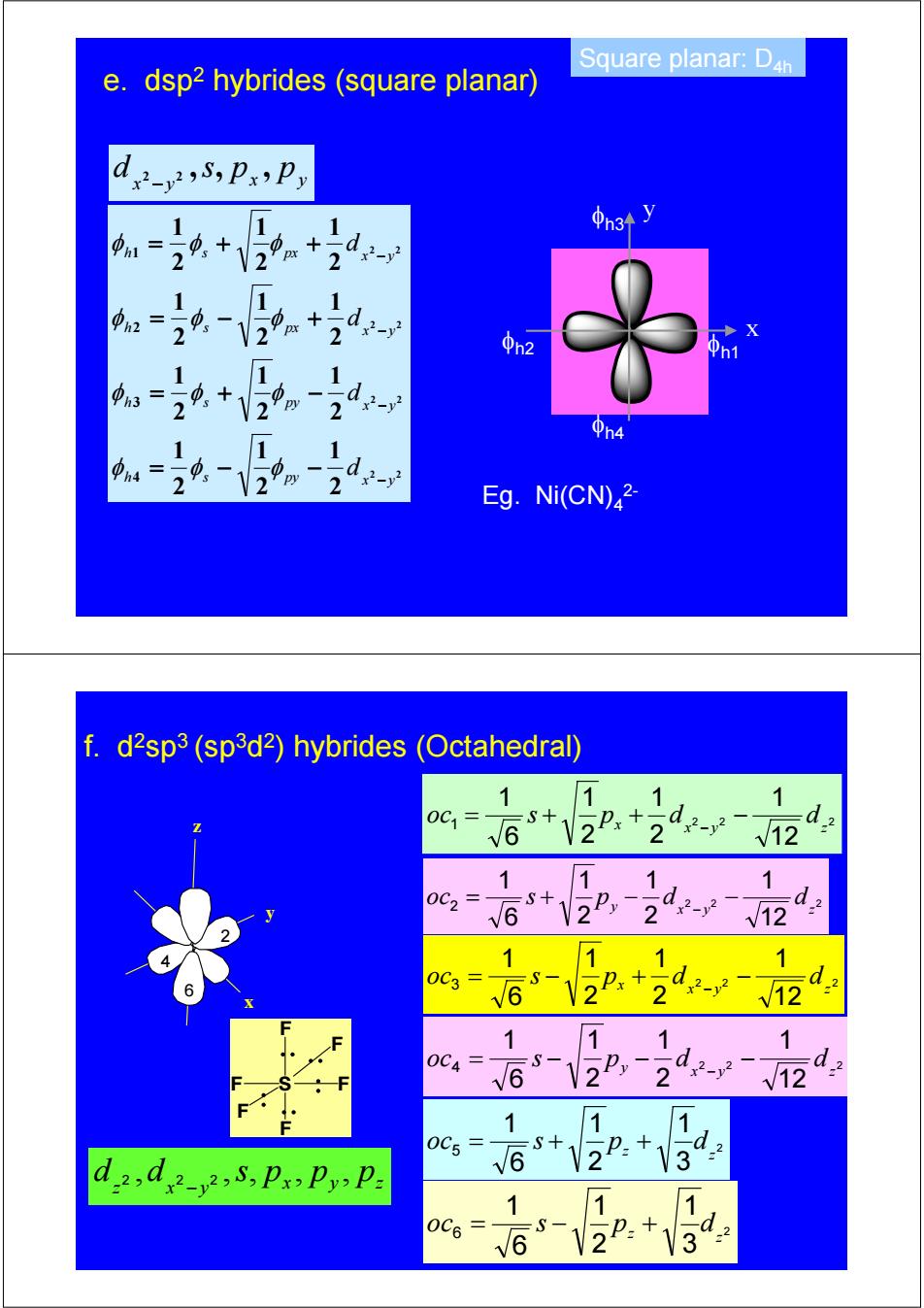
Square planar:D4h e.dsp2 hybrides (square planar) 中1= 9 d: φn2 h2 中n31 2 2 2 Eg.Ni(CN)2- f.d2sp3 (sp3d2)hybrides (Octahedral) 1 1 0G6+22.+24 V12 11 1 oc=65+12P, d2- 2V12 11 6-2+ -dz 1 11 oc=16-V2P,-2d2 1 0C5 =S十 d2 dd5,PxPyP= √ 1 1 0C6 √6 2P+3
Square planar: D4h 2 2 2 2 2 2 2 2 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 4 3 2 1 h s py x y py x y h s px x y h s px x y h s d d d d − − − − = − − = + − = − + = + + φ φ φ φ φ φ φ φ φ φ φ φ x y x y d 2 2 ,s, p , p − φh1 x y φh3 φh2 φh4 Eg. Ni(CN)4 2- e. dsp2 hybrides (square planar) 5 1 2 3 4 6 x y z 2 3 1 2 1 6 1 5 z z oc = s + p + d 2 2 2 12 1 2 1 2 1 6 1 1 x y z oc = s + px + d − d − 2 2 2 12 1 2 1 2 1 6 1 2 x y z oc = s + py − d − d − 2 2 2 12 1 2 1 2 1 6 1 3 x y z oc = s − px + d − d − 2 2 2 12 1 2 1 2 1 6 1 4 x y z oc = s − py − d − d − 2 3 1 2 1 6 1 6 z z oc = s − p + d x y z z x y d 2 ,d 2 2 ,s, p , p , p − f. d2sp3 (sp3d2) hybrides (Octahedral) F S F F F F F

Hybridization schemes spndm gives a“complete'”set of hybrid orbitals for“any”geometry. sp linear sp2 trigonal planar sp3 tetrahedral sp3d (d,2) trigonal bipyramidal sp3d(d,2-y2) square-based pyramidal sp3d2 octahedral sp2d square planar 3.The angle between two hybrid orbital spn hybridation 4n=Va02、+V1-a42p 中m=Va功,+V1-a,2n ,=Va中,+V1-a,4p whereφnmis 中p=X,中x+y,02py+2,02p
Hybridization schemes spndm gives a “complete” set of hybrid orbitals for “any” geometry. sp octahedral 3d2 sp trigonal bipyramidal 3d (dz 2) square-based pyramidal sp3d(dx 2-y 2) sp square planar 2d sp tetrahedral 3 sp trigonal planar 2 sp linear 3. The angle between two hybrid orbital spn hybridation h 2s 2 p φ = αφ + 1−αφ p j φh j = α j φ2s + 1−α j φ2 pi hi i 2s i 2 φ = α φ + 1−α φ p i px i py i pz x y z i φ = φ + φ2 + φ2 where φpi is

Normalization and orthogonality 0=∫44,dr=∫(Va4+V1-g)(Wa4,+V1-cgn)dr -aaSdr+(1-@)-@)o.dr+0+0 O-aa,+/(1-a)(-@,)cose aa V1-a)0-a) (c0s00,0>90°) Equivalent hybridzation.Example:CH4 i≠0j Non-equivalent hybridzation.Example:CHCl3,CHaCl Equivalent hybridization sp3-hybrides 1 Q= 4 1 aaj 4 1 V1-a,1-a) 3 4 sp3 0=10928" 109.5 109.5° 109.59 109.5
(1 )(1 ) cos 0 (1 )(1 ) cos (1 )(1 ) 0 0 0 ( 1 )( 1 ) 2 2 2 2 i j i j ij i j i j ij i j s i j pi pj hi hj i s i pi j s j pj d d d d α α αα θ αα α α θ αα φ τ α α φ φ τ φ φ τ αφ αφ α φ α φ τ − − =− = + − − = + − − + + = = + − + − ∫ ∫ ∫ ∫ Equivalent hybridzation. Example: CH4 Non-equivalent hybridzation. Example: CHCl3, CH3Cl i j i j α α α α ≠ = (cosθij<0, θij>90°) φ hi φ hj θ ij Normalization and orthogonality sp3 − hybrides 109 28" 3 1 4 3 4 1 (1 )(1 ) cos 4 1 0 = = − = − − − = − = θ α α α α θ α i j i j ij Equivalent hybridization