
Chapter 2 Atomic structure 2.1 The Schrodinger equation and its solution for one-electron atoms 2.1.1 The Schrodinger equation The Hamiltonian Operator of one-electron atoms H atom,He+and Li2+ =in+元+ne= 2mn n 2m。 V:+P-
Chapter 2 Atomic structure 2.1 The Schrödinger equation and its solution for one-electron atoms 2.1.1 The Schrödinger equation The Hamiltonian Operator of one-electron atoms H atom, He+ and Li2+ e n e e n n n e n e V m m H = T +T +V − = − ∇ − ∇ + − ˆ 2 2 ˆ ˆ ˆ ˆ 2 2 2 2 h h e N
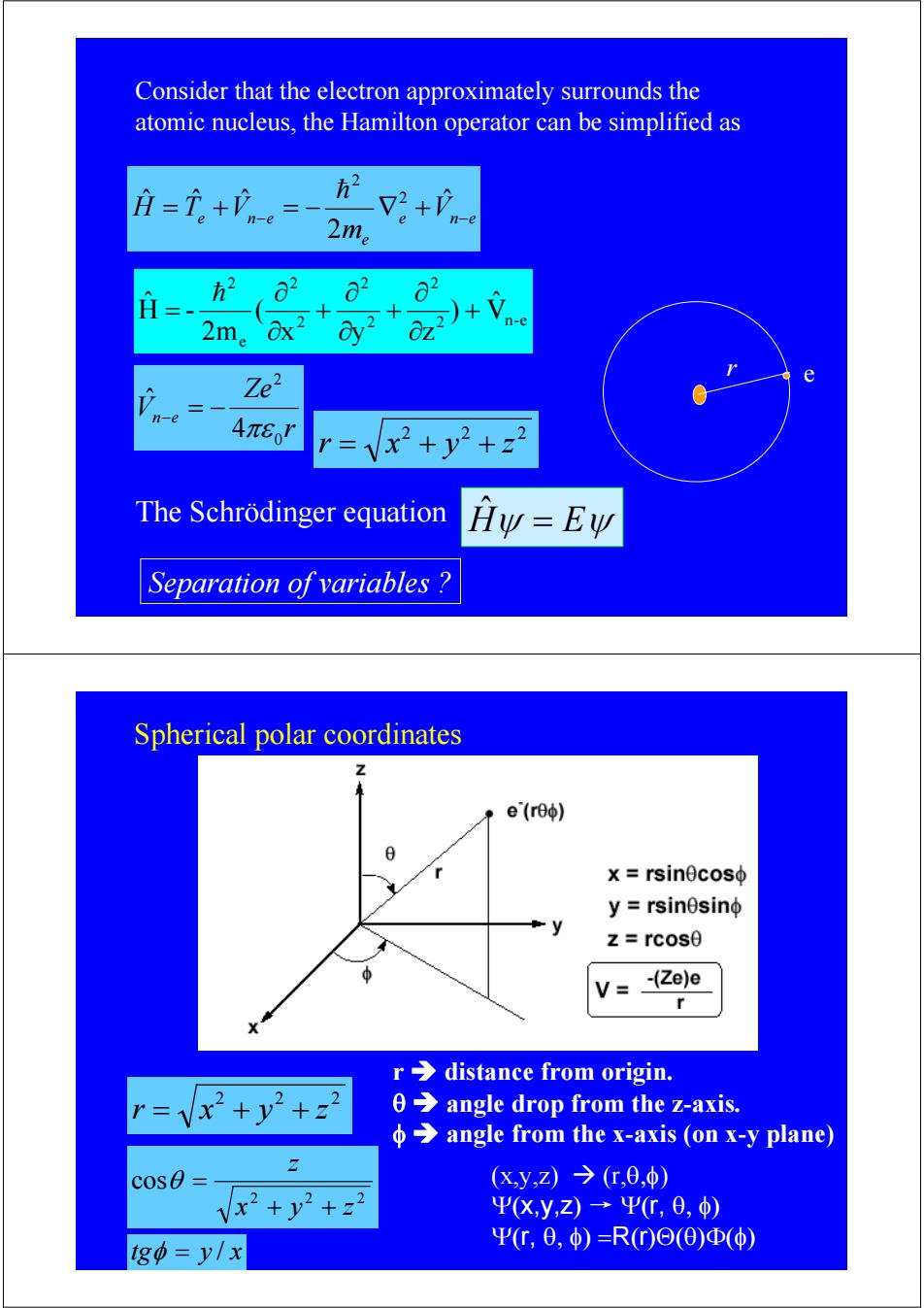
Consider that the electron approximately surrounds the atomic nucleus,the Hamilton operator can be simplified as =i。+n= 2+心 2m。 o2 62 2m。 2)+Vn-e OZ Ze2 e n-e 4πer r=Vx2+y2+z2 The Schrodinger equation Hy=Ew Separation of variables Spherical polar coordinates Z e(re) x rsinecoso y=rsinesinφ z=rcos0 V=_ (Ze)e r r>distance from origin. =Vx+y2+z2 0 angle drop from the z-axis. angle from the x-axis (on x-y plane) cos0= (x,y,Z)→(,0,φ) Vx2+y2+22 ΨX,y,z)→Ψr,6,) g中=y/x Ψr,0,φ)=R(r)Θ(Θ)Φ(φ)
e n e e e n e V m H = T +V − = − ∇ + − ˆ 2 ˆ ˆ ˆ 2 2 h r Ze Vn e 0 2 4 ˆ πε − = − Consider that the electron approximately surrounds the atomic nucleus, the Hamilton operator can be simplified as r e 2 2 2 r = x + y + z 2 n-e 2 2 2 2 2 e 2 Vˆ ) x y z ( 2m H - ˆ + ∂ ∂ + ∂ ∂ + ∂ ∂ = h Separation of variables ? The Schrödinger equation Hˆψ = Eψ Spherical polar coordinates 2 2 2 r = x + y + z (x,y,z) Æ (r,θ,φ) Ψ(x,y,z) → Ψ(r, θ, φ) Ψ(r, θ, φ) =R(r)Θ(θ)Φ(φ) r Î distance from origin. θ Î angle drop from the z-axis. φ Î angle from the x-axis (on x-y plane) 2 2 2 cos x y z z + + θ = tgφ = y / x

Spherical polar coordinates ar、aa0、op、a +( + Ox Ox op sine coso- cosecoso a sinΦ 0 r 00 rsine00 a 0 cos0sinφ a coso a sinsin 的 a a0 rsine dd sine 02 =Cos0. or a0 D2 1 1 (S11n7○ 1 o2 r2 ar Or r2 sine d0 a0' r2sin20062 Ze2 n-e (4πE)r The Schrodinger equation 1 1 a Ze2 (sin 十 ay8π2m(E+ )w=0 or r2sin 00 ae r2sin20862 h2 4π8' 2.1.2 The solution --separation of variables Substitute P(r,0,Φ)=R(r)⊙(O)Φ(φ)into the equation 1 )+7sin0 1 a 1 y8πm(E+ Or sn0c%+7sn900伊 Ze2 )w=0 a0 π8I and multiply with r2 R(r)Θ(0)Φ(φ) 1 1 (sin 1 )+ R(r)ar (0)sine a0 a0 ao0+8(E+4 ()sin20 02 h2 e2r2=0 1 0 2aR(r)、, 8m(E AnEo ze 1 R(r)or Or h2 er=o0)sino o0 (sin) 1 aΦ() + a01 Φ()sin20ap2
Spherical polar coordinates () ( ) ( ) r x xr x xp θ φ θ ∂ ∂∂ ∂ ∂ ∂ ∂ =+ + ∂ ∂∂ ∂∂ ∂∂ cos cos sin sin cos rr rsin θ φ φ θ φ θ θ φ ∂ ∂ ∂ =+ − ∂ ∂∂ cos sin cos sin sin y rr rsin θ φ φ θ φ θ θ φ ∂ ∂ ∂∂ = + ⋅+ ⋅ ∂ ∂ ∂∂ θ θ θ ∂ ∂ − ⋅ ∂ ∂ = ∂ ∂ z r r sin cos 2 2 2 2 2 2 2 2 sin 1 (sin ) sin 1 ( ) 1 θ θ φ θ θ θ ∂ ∂ + ∂ ∂ ∂ ∂ + ∂ ∂ ∂ ∂ ∇ = r r r r r r 2 0 (4 ) n e Ze V πε r − = − The Schrödinger equation 2 2 2 2 2 2 22 2 2 0 11 1 8 ( ) (sin ) ( ) 0 sin sin 4 me Ze r E rr r r r h r ψ ψψ π θ ψ θ θ θ θ φ πε ∂∂ ∂ ∂ ∂ + + + += ∂∂ ∂ ∂ ∂ 2.1.2 The solution --- separation of variables Substitute Ψ(r, θ, φ) =R(r)Θ(θ)Φ(φ) into the equation 2 2 2 2 2 2 22 2 2 0 11 1 8 ( ) (sin ) ( ) 0 sin sin 4 me Ze r E rr r r r h r ψ ψψ π θ ψ θ θ θ θ φ πε ∂∂ ∂ ∂ ∂ + + + += ∂∂ ∂ ∂ ∂ and multiply with ( ) ( ) ( ) 2 R r Θ θ Φ φ r ) 0 4 ( ( ) 8 ( )sin 1 ) ( ) (sin ( )sin 1 ) ( ) ( ( ) 1 2 0 2 2 2 2 2 2 2 + + = ∂ ∂ Φ Φ + ∂ ∂Θ ∂ ∂ Θ + ∂ ∂ ∂ ∂ r r ze E h m r R r r R r r e πε π φ φ θ φ θ θ θ θ θ θ ] ( ) ( )sin 1 ) ( ) (sin ( )sin 1 ) [ 4 ( 8 ) ( ) ( ( ) 1 2 2 2 2 0 2 2 2 2 φ φ θ φ θ θ θ πε θ θ θ π ∂ ∂ Φ Φ + ∂ ∂Θ ∂ ∂ Θ + + = − ∂ ∂ ∂ ∂ r r ze E h m r R r r R r r e

1 8(rOR(r)+8'm (E+e e)r2=[ 10 (sin8(0、 aΦ(p) R(r) 4πEJ (0)sine a0 a0 Φ()sin20ap2 1(r) ze- let 8πm(E+ )r2=B R(r)Or h2 Radial part,R eq. 4πE1 1 a (sin() 1 a2D() =-B Angular part ⊙(0)sin0aa a0 Φ()sin20ap2 multiplied sin20 sine (sin 1 ()=-Bsin20 ⊙(0)a 60 Φ()ab2 sine o (sin() +Bsin20=- 1 aΦ() ⊙()a8 a0 ()ap2 sin0 let (sin() +Bsin20=m2 Θ(0)a a0 p©eq. 1 ∂Φ() 三-ml DΦ Φ()a2 eq. a.Φ(b)equation d2Φ(p) dd +m2Φ()=0 Its complex form: Φ=Aetilml№,letm=±ml,Φ=Aem Normalization 2 ΦΦdΦ-=4eme地=l 1 A= V2π 1 m -cosm+- -sin mo V2元 √2 2 Φm(φ)=Φm(p+2π The values of m must be eim(+2r)=eimp.em2r m=0,±1,±2, =1 m magnetic quantum cos2mπ+isin2mn=1 number
β πε π + + = ∂ ∂ ∂ ∂ 2 0 2 2 2 2 ) 4 ( 8 ) ( ) ( ( ) 1 r r ze E h m r R r r R r r let e ] ( ) ( )sin 1 ) ( ) (sin ( )sin 1 ) [ 4 ( 8 ) ( ) ( ( ) 1 2 2 2 2 0 2 2 2 2 φ φ θ φ θ θ θ πε θ θ θ π ∂ ∂ Φ Φ + ∂ ∂Θ ∂ ∂ Θ + + = − ∂ ∂ ∂ ∂ r r ze E h m r R r r R r r e f Angular part f Radial part, R eq. β φ φ θ φ θ θ θ θ θ θ = − ∂ ∂ Φ Φ + ∂ ∂Θ ∂ ∂ Θ 2 2 2 ( ) ( )sin 1 ) ( ) (sin ( )sin 1 β θ φ φ θ φ θ θ θ θ θ θ 2 2 2 2 sin ( ) ( ) 1 ) ( ) (sin ( ) sin sin = − ∂ ∂ Φ Φ + ∂ ∂Θ ∂ ∂ Θ multiplied 2 2 2 ( ) ( ) 1 ) sin ( ) (sin ( ) sin φ φ φ β θ θ θ θ θ θ θ ∂ ∂ Φ Φ + = − ∂ ∂Θ ∂ ∂ Θ 2 2 ) sin ( ) (sin ( ) sin let + = m ∂ ∂Θ ∂ ∂ Θ β θ θ θ θ θ θ θ 2 2 2 ( ) ( ) 1 = −m ∂ ∂ Φ Φ φ φ φ fΘ eq. fΦ eq. a. Φ(φ) equation Its complex form: Φ =Ae±i|m|φ , let m= ±|m|, Φ =Aeim φ ( ) 0 ( ) 2 2 2 + Φ = Φ φ φ φ m d d 1 2 2 0 2 0 * Φ Φ Φ = Φ = − ∫ ∫ d A e e d Normalization im im m m φ φ π π Φ (φ) = Φ (φ + 2π ) m m The values of m must be m = 0,±1,±2,⋅⋅⋅⋅⋅⋅ m : magnetic quantum number 2π 1 A = φ π φ π π φ m i e m im m sin 2 cos 2 1 2 1 Φ = = + imφ im(φ 2π ) imφ im2π e = e = e ⋅e + cos 2 sin 2 1 1 2 + = = π π π m i m eim

complex function Φn=Aemo (m=0,±1,±2,…) Usually,real functions are used,which are deduced from the complex function according to the assumption of the linear combination of these states Aeo=Acosmo+iAsinmo -m=Ae mo=Acosmo-iAsin mo ④D1=Φm+①-m=2Ac0smp=Bcosmp Φ2=Φm-Φm=2 iAsin mo=B'sinmo m normalization condition 1 (2 (Bcosmo)2dΦ=B2π=1 Φ Jo ΦΦdΦ= cosmo B sinmo Table The solution ofΦ(φ)equation m complex form real form 1 1 0 Φ0=1 2元 D022r 1 ①1= cos √2π Vπ 1 Φ1= e ip Φ= 1 sin √2元 Vπ 1 1 2 Φ2= cos20 √2π Φ= Vπ -2= Φ -sin 20 √2π Vπ
ϕ ϕ ϕ ϕ iA m B m A m B m m m m m 2 sin 'sin 2 cos cos 2 1 Φ = Φ − Φ = = Φ = Φ + Φ = = − − Usually, real functions are used, which are deduced from the complex function according to the assumption of the linear combination of these states . complex function Φ = Ae (m = 0,±1,±2,⋅⋅⋅⋅⋅⋅) im m ϕ ϕ ϕ ϕ ϕ ϕ ϕ Ae A m iA m Ae A m iA m im m im m cos sin cos sin Φ = = − Φ = = + − − π ϕ π π π 1 ( cos ) 1 2 2 2 0 1 * 1 2 0 = Φ Φ Φ = Φ = = ∫ ∫ B d B m d B normalization condition ϕ π ϕ π m m sin 1 cos 1 2 1 Φ = Φ = Table The solution of Φ(φ) equation ϕ π π ϕ π π ϕ π π ϕ π π π π ϕ ϕ ϕ ϕ sin 2 1 2 1 2 cos 2 1 2 1 2 sin 1 2 1 1 cos 1 2 1 1 2 1 2 1 0 sin 2 2 2 cos 2 2 2 sin 1 1 cos 1 1 0 0 − Φ = Φ = Φ = Φ = − Φ = Φ = Φ = Φ = Φ = Φ = ± − − ± ± − − ± i i i i e e e e m complex form real form