
Chapter 8 The structures and properties of metals and alloys 8.1 The metallic bond and the general properties of metals 8.1.1 The "free-electron"model of the metallic bond The Schrodinger equation for the "free electrons"is V2y+[8π2m]/h2]Evw=0 V=0 Er=5.04*10-19 J or 3.15eV (for Na) Experimental value 3.2 eV 8.1.2 The band theory of solids Considering the electrons in metals moving in a periodic potential field of the metal atoms,the Schrodinger equation is (-h2/[8π2m]72+V)w=Ey Insulator: Metal: Semiconductor: Empty band Thermally Conduction band excited electrons Band gap Eg≥5eV “Bandgap' Eg<3eV Empty states: Filled band Valence band "holes'” Partially filled bands ---conduction bands
Chapter 8 The structures and properties of metals and alloys 8.1 The metallic bond and the general properties of metals 8.1.1 The “free-electron” model of the metallic bond The Schrödinger equation for the “free electrons” is ∇2ψ + [8π2m]/h2]Eψ=0 EF = 5.04*10-19 J or 3.15eV (for Na) Experimental value 3.2 eV V=0 8.1.2 The band theory of solids Considering the electrons in metals moving in a periodic potential field of the metal atoms, the Schrodinger equation is (-h2/[8π2m] ∇2+ V) ψ = Eψ Band gap Partially filled bands ---- conduction bands Eg≥5eV Eg<3eV Empty band Filled band
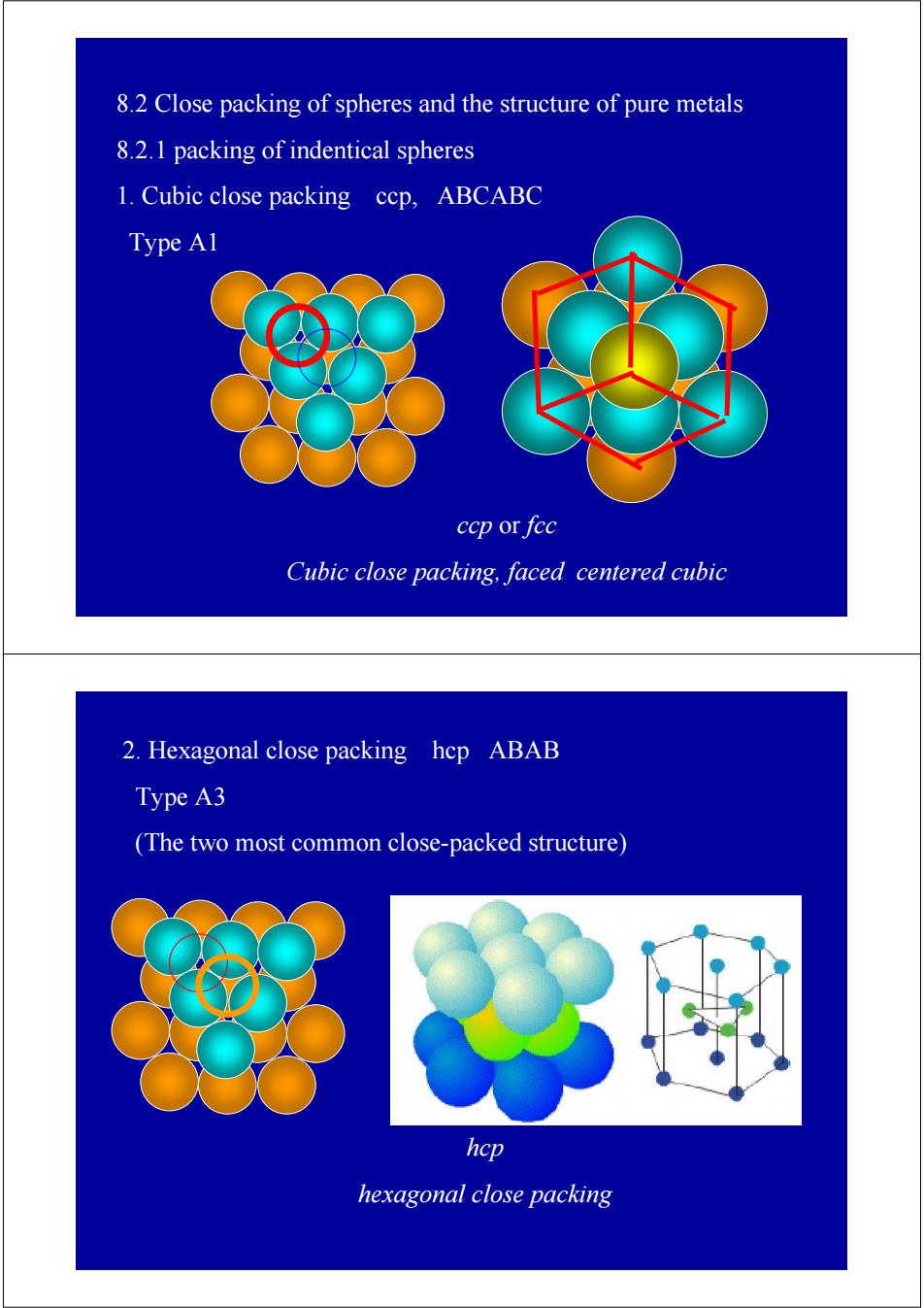
8.2 Close packing of spheres and the structure of pure metals 8.2.1 packing of indentical spheres 1.Cubic close packing ccp,ABCABC Type A1 ccp or fcc Cubic close packing,faced centered cubic 2.Hexagonal close packing hcp ABAB Type A3 (The two most common close-packed structure) 多胶 hcp hexagonal close packing
8.2 Close packing of spheres and the structure of pure metals 8.2.1 packing of indentical spheres 1. Cubic close packing ccp, ABCABC Type A1 ccp or fcc Cubic close packing, faced centered cubic 2. Hexagonal close packing hcp ABAB Type A3 (The two most common close-packed structure) hcp hexagonal close packing
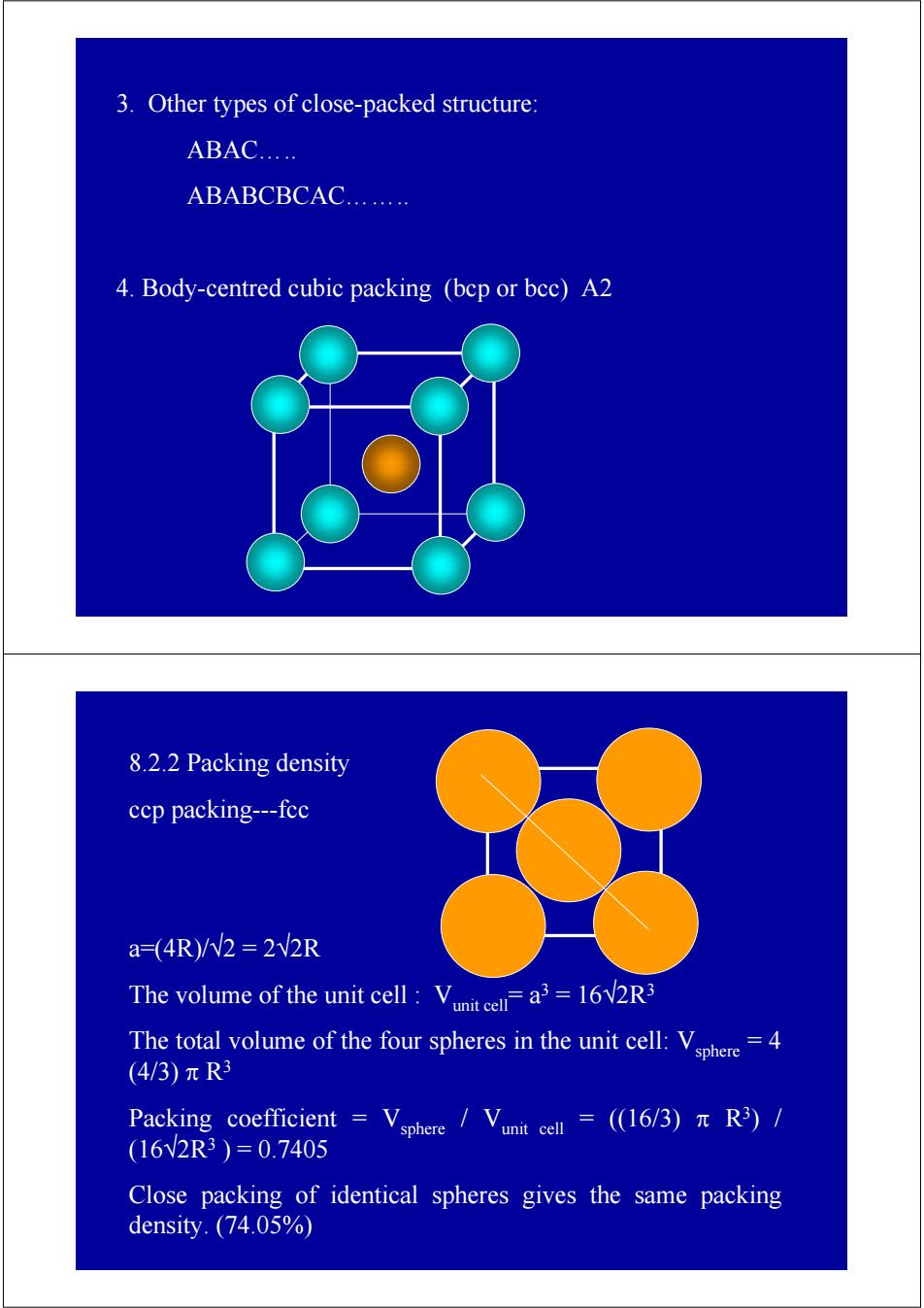
3.Other types of close-packed structure: ABAC..… ABABCBCAC........ 4.Body-centred cubic packing (bep or bec)A2 8.2.2 Packing density ccp packing---fcc a=(4R)/W2=2V2R The volume of the unit cell:Va=16V2R3 The total volume of the four spheres in the unit cell:Vhere=4 (4/3)πR3 Packing coefficient Vsphere ,/Vunit cell=(16/3)πR)/ (16V2R3)=0.7405 Close packing of identical spheres gives the same packing density.(74.05%)
3. Other types of close-packed structure: ABAC….. ABABCBCAC…….. 4. Body-centred cubic packing (bcp or bcc) A2 8.2.2 Packing density ccp packing---fcc a=(4R)/√2 = 2√2R The volume of the unit cell : Vunit cell= a3 = 16√2R3 The total volume of the four spheres in the unit cell: Vsphere = 4 (4/3) π R3 Packing coefficient = Vsphere / Vunit cell = ((16/3) π R3) / (16√2R3 ) = 0.7405 Close packing of identical spheres gives the same packing density. (74.05%)
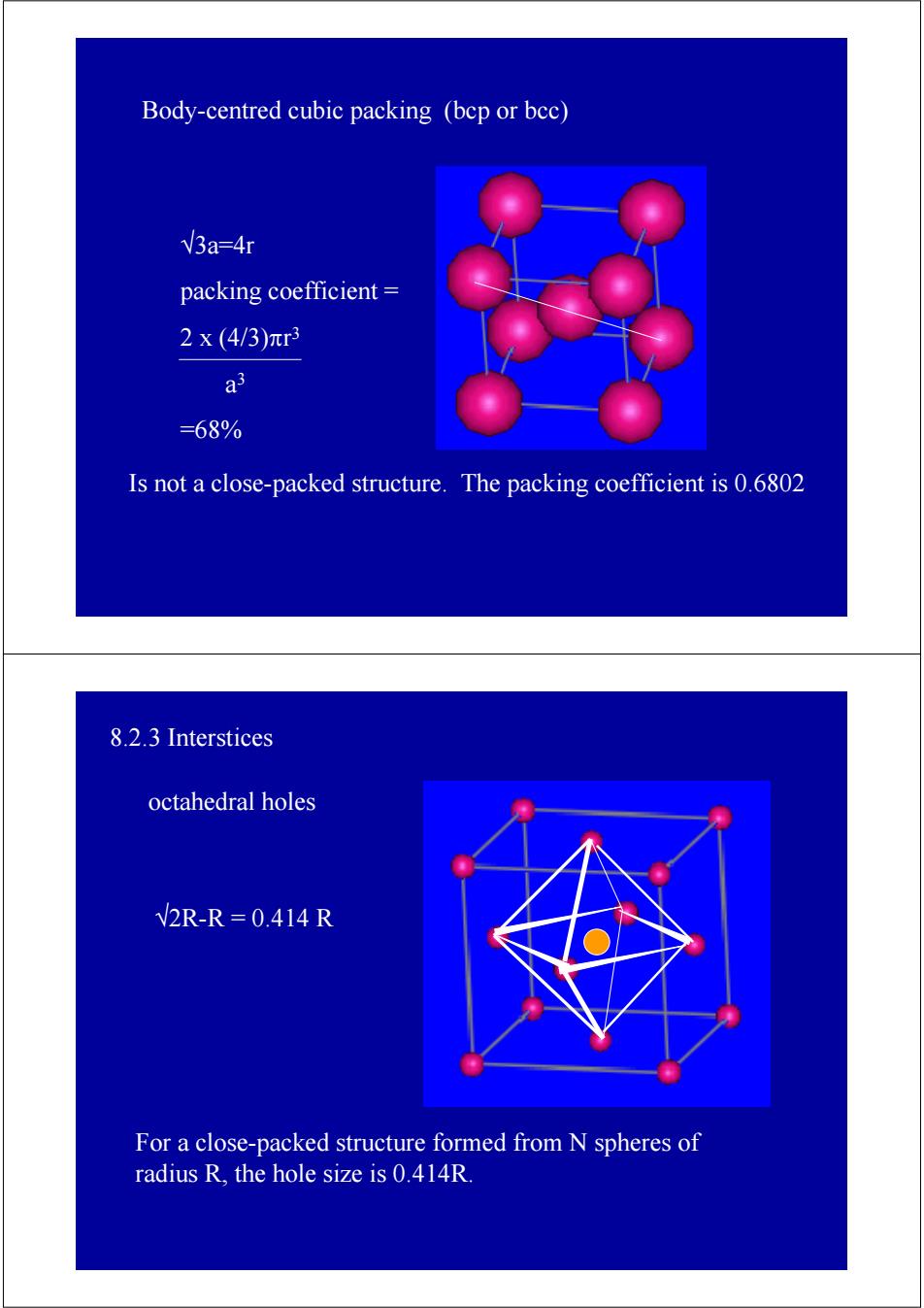
Body-centred cubic packing (bcp or bec) V3a-4r packing coefficient 2x(4/3)πr3 a =68% Is not a close-packed structure.The packing coefficient is 0.6802 8.2.3 Interstices octahedral holes V2R-R=0.414R For a close-packed structure formed from N spheres of radius R,the hole size is 0.414R
Body-centred cubic packing (bcp or bcc) Is not a close-packed structure. The packing coefficient is 0.6802 √3a=4r packing coefficient = 2 x (4/3)πr3 a3 =68% 8.2.3 Interstices For a close-packed structure formed from N spheres of radius R, the hole size is 0.414R. octahedral holes √2R-R = 0.414 R
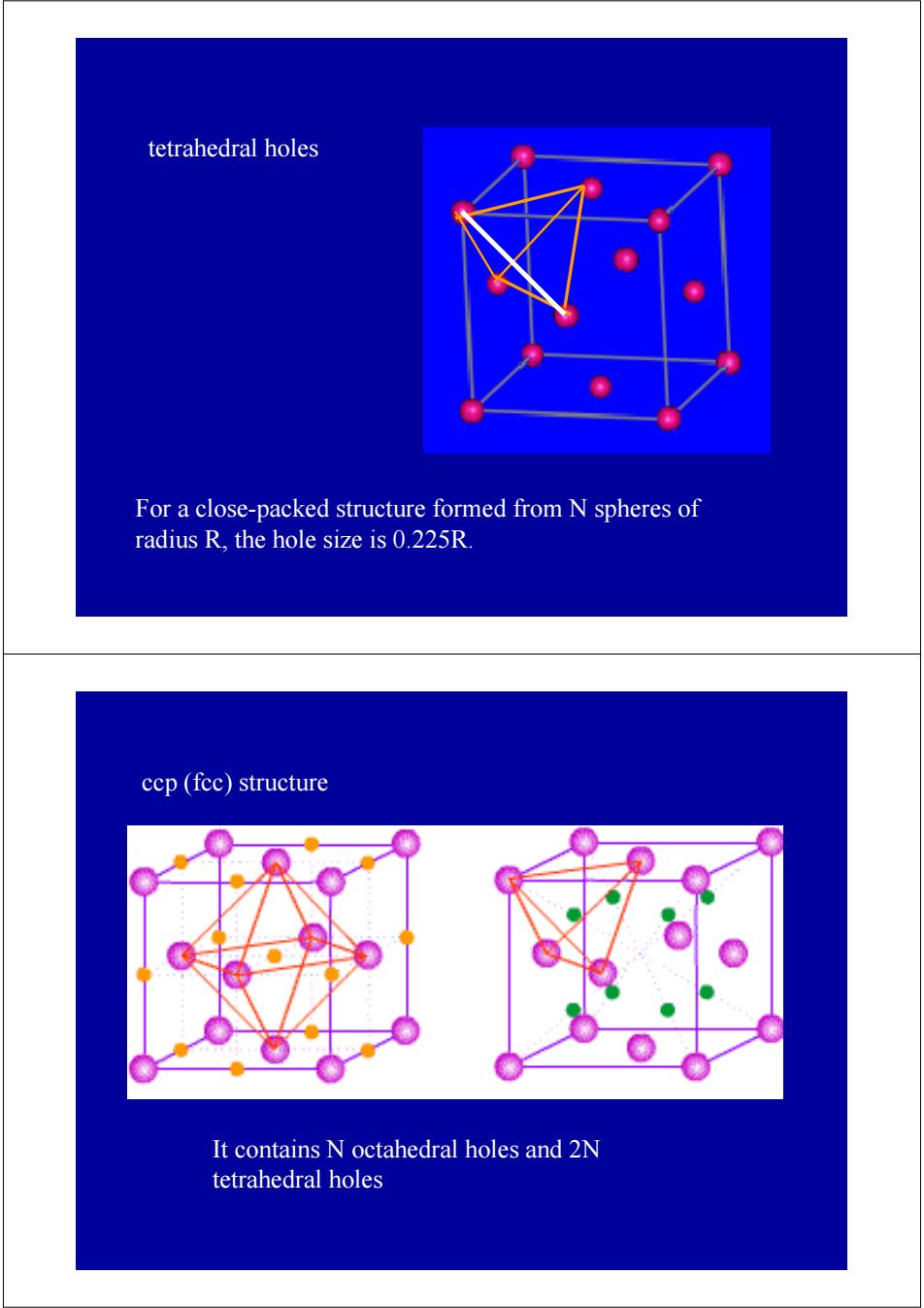
tetrahedral holes For a close-packed structure formed from N spheres of radius R,the hole size is 0.225R. ccp(fec)structure It contains N octahedral holes and 2N tetrahedral holes
For a close-packed structure formed from N spheres of radius R, the hole size is 0.225R. tetrahedral holes It contains N octahedral holes and 2N tetrahedral holes ccp (fcc) structure