《理论力学》课程教学资源（PPT课件）动量定理

py =2m Vc cos wt +mvc cos ot +mvB lo 2mo comco+m.2lo.coso (5m +4m.)cosot y 所以机构动量的大小和方向为 p=+-(5m+4m） B 2% cos(元，i)=cosP:=sinot p

m m t l t m l t l m l t m p m v t m v t m v y C C B           (5 4 ) cos 2 cos 2 cos 2 2 cos 2 cos cos 1 2 1 1 2 1 1 1 2         所以机构动量的大小和方向为 (5 4 ) 2 1 2 2 2 m m l p  px  py    t p p p i x cos( , )  cos  sin   x y O t  C C A B C1 B m v  2 A m v  2 C m v  2 1 1 C1 m v 

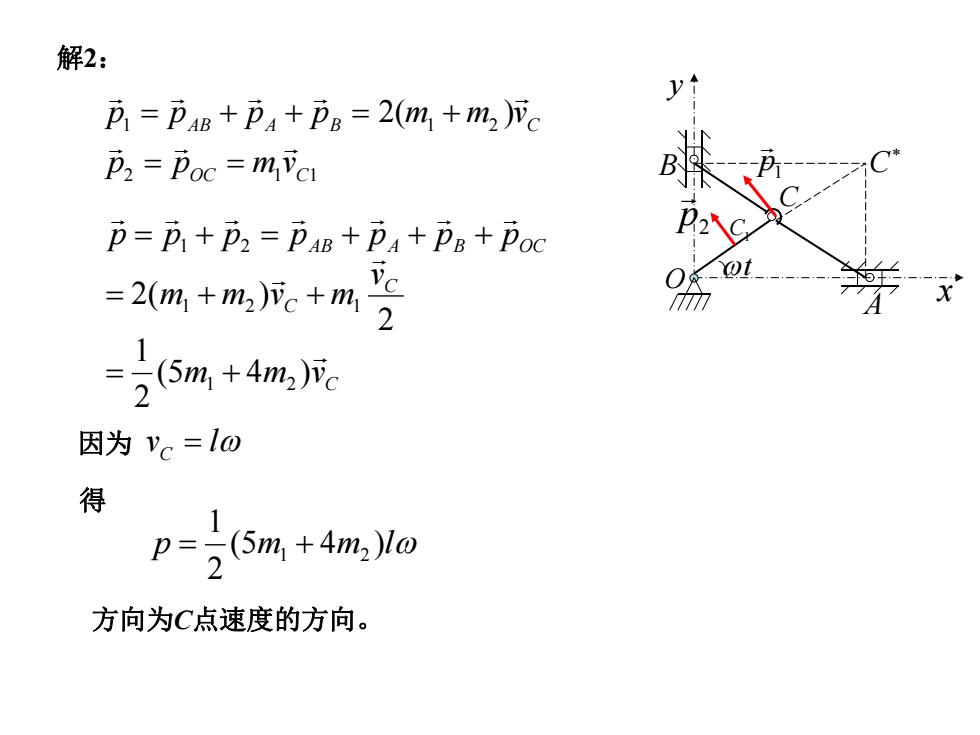
解2： y D PaB +Pa+Pe=2(m+m2)c P2=Poc =mVc B p=p+p2=PaB +Pa+PB+Poc C =2m,+m)成e+m2 =5m+4m城 因为vc=lo 得 p=25m+4m,l0 方向为C点速度的方向

x yO t  C C A B C1 1 p p2  C C C AB A B OC m m v v m m v m p p p p p p p           (5 4 ) 21 2 2( ) 1 2 1 2 1 1 2            解2：1 1 2 2 1 1 2( ) AB A B C OC C p p p p m m v p p m v                vC  l p (5m 4m )l 21  1  2 方向为C点速度的方向。 因为得

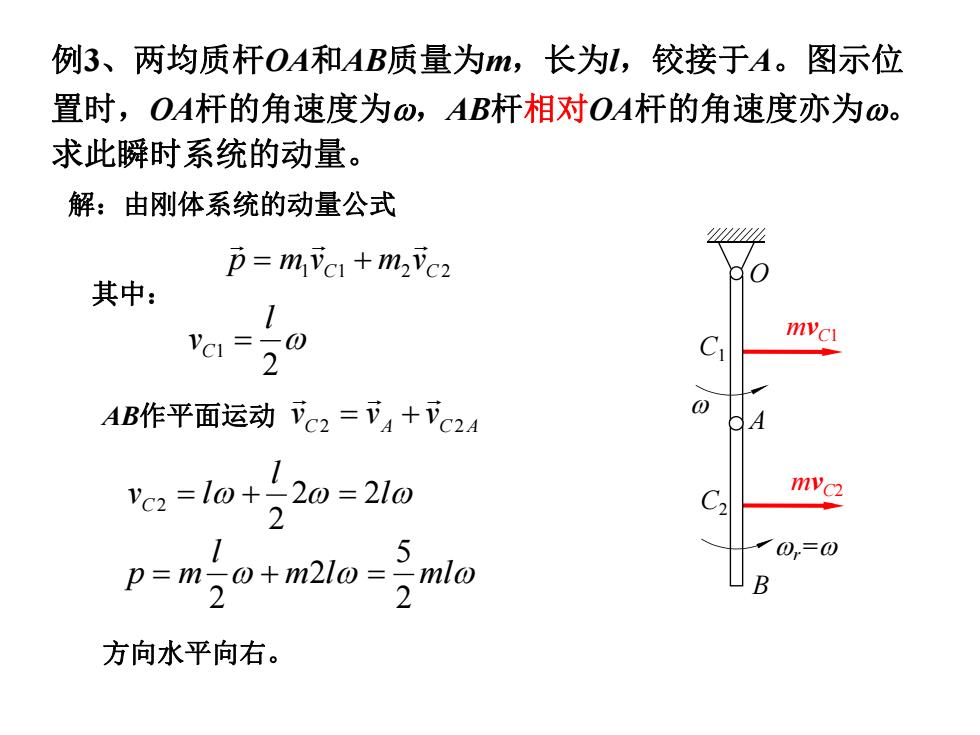
例3、两均质杆OA和AB质量为m,长为L,铰接于A。图示位 置时，OA杆的角速度为0，AB杆相对OA杆的角速度亦为o. 求此瞬时系统的动量。 解：由刚体系统的动量公式 p=mVc+m2vc2 其中： 1 'c1=50 mycI 2 AB作平面运动币c2=下4+c2A vc2=10+20=2lo myc2 2 C2 「0=0 p=m20+m210=2mla B 方向水平向右

例3、两均质杆OA和AB质量为m，长为l，铰接于A。图示位 置时，OA杆的角速度为，AB杆相对OA杆的角速度亦为。 求此瞬时系统的动量。 解：由刚体系统的动量公式 1 C1 2 C2 p m v m v      其中：  2 1 l vC    l l v l C 2 2 2 2     m l ml l p m 2 5 2 2    方向水平向右。 mvC1 mvC2 O A B C1 C2  r= C A C A v v v 2 2    AB作平面运动  

10.1动量与冲量 10.1.2冲量 作用力与作用时间的乘积称为常力的冲量。 冲量是矢量，方向与力的方向一致。冲量的单位为NS, 与动量的量纲相同。 •常力的冲量 i-F 变力的冲量一元冲量 dI=Fdt 而力F在作用时间内的冲量是矢量积分 I=fFdr

10.1 动量与冲量 10.1.2 冲量 作用力与作用时间的乘积称为常力的冲量。 冲量是矢量，方向与力的方向一致。冲量的单位为N•s， 与动量的量纲相同。 •常力的冲量 I  Ft   •变力的冲量－元冲量 d I  F d t   而力F 在作用时间 内的冲量是矢量积分  t 0 d t  t  I F  

10.2动量定理 10.2.1质点的动量定理 d d ma m- （m)=F 'dt dt d(mv)=Fdt=dI 微分形式 质点动量的增量等于作用于质点上的力的元冲量。 mw-m,=∫Fdt=i 积分形式 在某一时间间隔内，质点动量的变化等于作用于质 点的力在此段时间内的冲量

10.2.1 质点的动量定理 质点动量的增量等于作用于质点上的力的元冲量。 d(mv)  F d t  d I    微分形式 10.2 动量定理 在某一时间间隔内，质点动量的变化等于作用于质 点的力在此段时间内的冲量。 0 0 d t m  m  t   v v F I     积分形式 d d ( ) d d m m m t t    v a v F    