8.1刚体平面运动概述和运动分解 对于任意的平面运动, 可在平面图形上任取一点O', 称为基点。在这一点假想地 安上一个平移参考条Oxy'; 平面图形运动时,动坐标轴 方向始终保持不变,可令其 分别平行于定坐标轴Ox和 Oy。于是平面图形的平面 o' 运动可看成为随同基点的平 移和随基点转动这两部分运 动的合成
8.1 刚体平面运动概述和运动分解 对于任意的平面运动, 可在平面图形上任取一点O' , 称为基点。在这一点假想地 安上一个平移参考系O'x'y'; 平面图形运动时,动坐标轴 方向始终保持不变,可令其 分别平行于定坐标轴Ox和 Oy 。于是平面图形的平面 运动可看成为随同基点的平 移和随基点转动这两部分运 动的合成。 y' O x' ' y x O
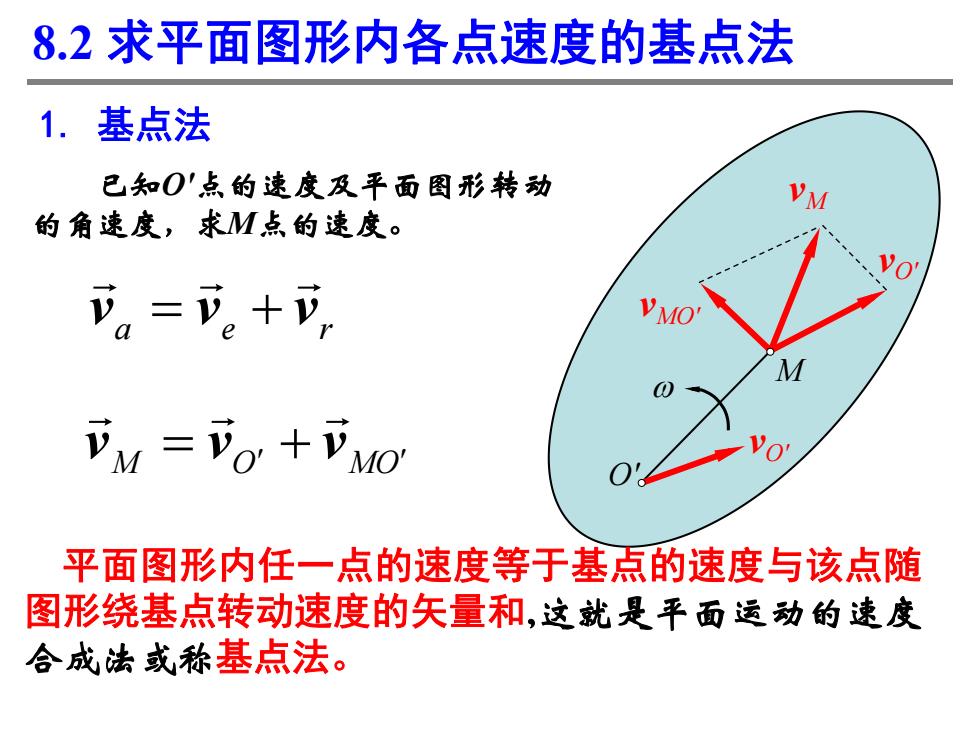
8.2求平面图形内各点速度的基点法 1.基点法 已知O'点的速度及平面图形转动 的角速度,求M点的速度。 可a=可。+, M=O+MO 平面图形内任一点的速度等于基点的速度与该点随 图形绕基点转动速度的矢量和,这就是平面运动的速度 合成法或称基点法
O' M 平面图形内任一点的速度等于基点的速度与该点随 图形绕基点转动速度的矢量和,这就是平面运动的速度 合成法或称基点法。 1. 基点法 已知O'点的速度及平面图形转动 的角速度,求M点的速度。 8.2 求平面图形内各点速度的基点法 w vM vO' vMO' vO' a e r v v v M O MO v v v

例1椭圆规机构如图。已知连杆AB的长度l=20cm,滑块A 的速度v4=10cm/s,求连杆与水平方向夹角为30°时,滑块 B和连杆中点M的速度。 解:AB作平面运动,以A为基点, VB 分析B点的速度。 VBA Va =VA+Vad VA AB 由图中几何关系得: M Vg =v cot 30=10v3 cm/s 309 VBA= =20cm/s sin30° 4-lrad/s方向如图所示。 1
例1 椭圆规机构如图。已知连杆AB的长度l = 20 cm,滑块A 的速度vA=10 cm/s ,求连杆与水平方向夹角为30°时,滑块 B和连杆中点M的速度。 解: AB作平面运动,以A为基点, 分析B点的速度。 cot 30 10 3 cm/s B A v v 由图中几何关系得: 1rad s BA AB v l w 方向如图所示。 A vA vA vB vBA B wAB 30° B A BA v v v M 20 cm/s sin 30 A BA v v 30°
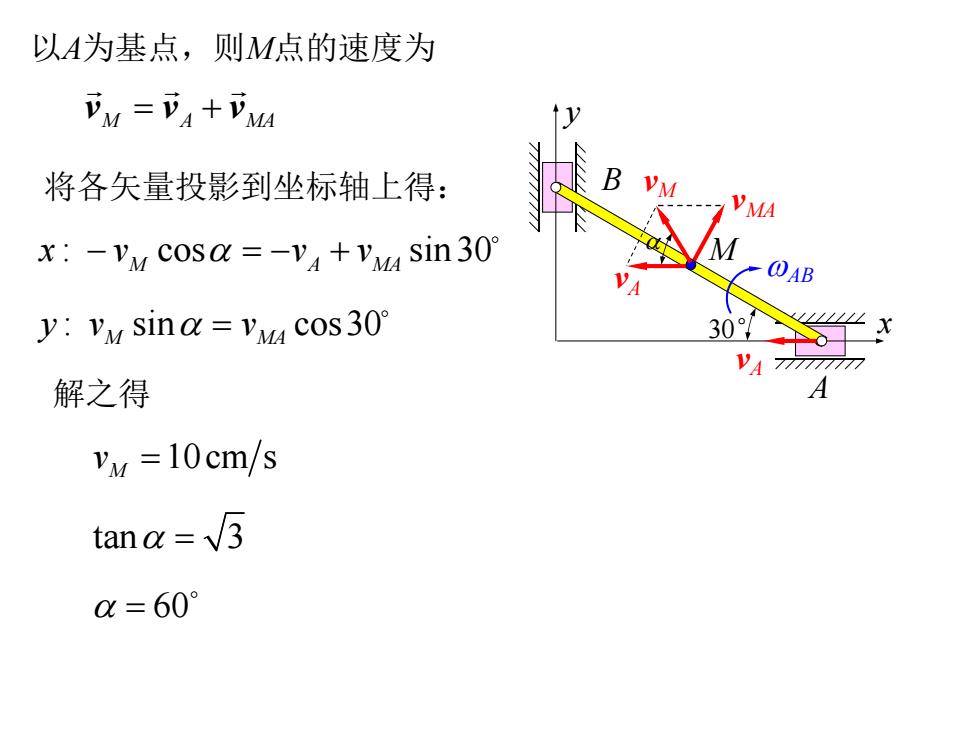
以A为基点,则M点的速度为 下M=A+MM 将各矢量投影到坐标轴上得: xX:-Vu cosa =-V+Vva sin 30 y:Vy sina=VMa cos30° 30°, 解之得 Vy =10cm/s tana=√3 =60°
以A为基点,则M点的速度为 将各矢量投影到坐标轴上得: : cos sin 30 M A MA x v v v : sin cos30 M MA y v v 解之得 10cm s M v tan 3 60 A vA vA vMA B wAB 30° M vM M A MA v v v x y

例2行星轮系机构如图。大齿轮固定,半径为1;行星齿轮沿 轮I只滚而不滑动,半径为r2。系杆OA角速度为oo。求轮II的角 速度ou及其上B,C两点的速度。 解:行星齿轮I作平面运动,求得A 点的速度为 B v4=0oOA=0o(+3) 以A为基点,分析两轮接触点D的 速度。 VDA VD =VA+VDA 由于齿轮I固定不动,接触点D不 滑动,显然yD=0,因而有ypA=vA =oo(r1tr2),方向与y4相反,VDA 为点D相对基点A的速度,应有DA =0IDA。所以 Vp4=0o(G+5) DA 3
例2 行星轮系机构如图。大齿轮I固定,半径为r1;行星齿轮II沿 轮I只滚而不滑动,半径为r2。系杆OA角速度为wO。求轮II的角 速度wII及其上B,C两点的速度。 解:行星齿轮II作平面运动,求得A 点的速度为 vA wO D A DA v v v O D A B C vA vDA wII I II 以A为基点,分析两轮接触点D的 速度。 1 2 ( ) A O O v w OA w r r 由于齿轮I固定不动,接触点D不 滑动,显然vD=0,因而有vDA=vA =w O(r1+r2),方向与vA相反,vDA 为点D相对基点A的速度,应有vDA =wII·DA。所以 1 2 II 2 ( ) DA O v r r DA r w w