电子科技大学：《导波场论 Field Theory of Guided Waves》课程教学资源（课件讲稿）第三章 谐振腔理论（5/5）

导波场论 回顾分离变量法 谐振腔中的应用 时间变量 坐标变量，模式函数，坐标的函数，场强度位置分布 V2En+k2E。=0 V2i。+ki。=0 H-r Ea及Ha边界条件 与上类似分离不同分量，某一分量不同坐标的二阶微分，有 E(u,v,==U,(u)v,(v)Z:(= 1 2.9=k Z.(z）az a何-发间= 求解二阶微分 +k+2=8,4,· 再由边界条件求出三个K,由波数守恒关系求出谐振频率

导 波 场 论 回顾 分离变量法 谐振腔中的应用 a a b b a b a a b b a b E p E q F H r H s G         时间变量 坐标变量，模式函数，坐标的函数，场强度位置分布 2 2 2 2 + 0 0 a a a a a a E k E H k H      Ea及Ha边界条件 与上类似分离不同分量，某一分量不同坐标的二阶微分，有 E u v z az  , ,     U u V v Z z u v z           2 2 2 1 z z z Z z k Z z z          1 2 2 u u u u U u k U u        1 2 2 v v v v V v k V v   求解二阶微分 再由边界条件求出三个K ，由波数守恒关系求出谐振频率 2 2 2 2 u v z r r 0 k k k k       

例 课后作业 用模式函数法求解圆柱谐振腔（直径为D,高度为L)中 TEo11、TMo10模的谐振频率、场分布及储能

课后作业 用模式函数法求解圆柱谐振腔（直径为D，高度为L）中 TE011、TM010模的谐振频率、场分布及储能

复习小孔耦合 >等效磁流定理 Pn=Hon Hs E。=∑anE, z>0 法向磁场 jm=-nxE。 i=∑a,H, z>0 切向电场 E。=∑bE z<0 H。=∑bnHn z<0 口径Sa E、H E1、H1 Z

复习 小孔耦合  等效磁流定理 0 m s m s n H J n E        法向磁场 切向电场 + + - - 0 0 0 0 s n n s n n s n n s n n E a E z H a H z E b E z H b H z             ， ， ， ， E1、H1 Z 口径Sa Es、Hs

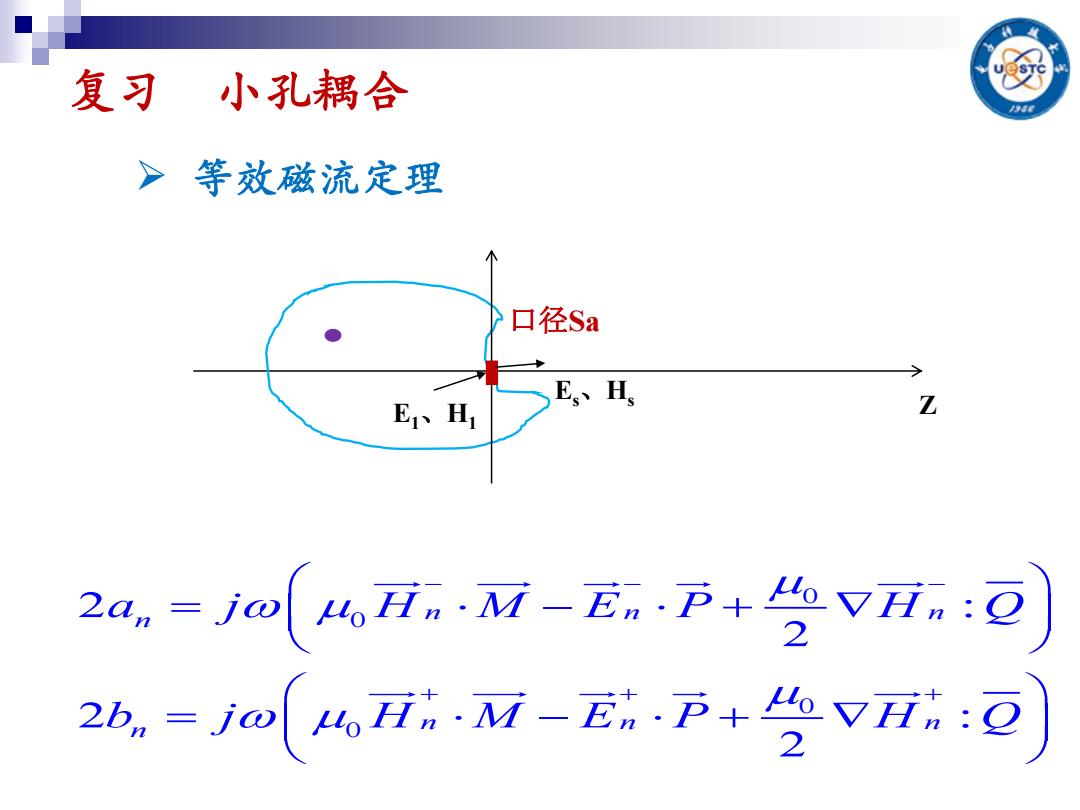
复习小孔耦合 >等效磁流定理 口径Sa E、H E1、H1 Z 2a,=m(%i.7-En+空vn可 2h,=m(uH.M-E万台vH:o

复习 小孔耦合  等效磁流定理 0 0 0 0 2 : 2 2 : 2 n n n n n n n n a j H M E P H Q b j H M E P H Q                                     E1、H1 Z 口径Sa Es、Hs

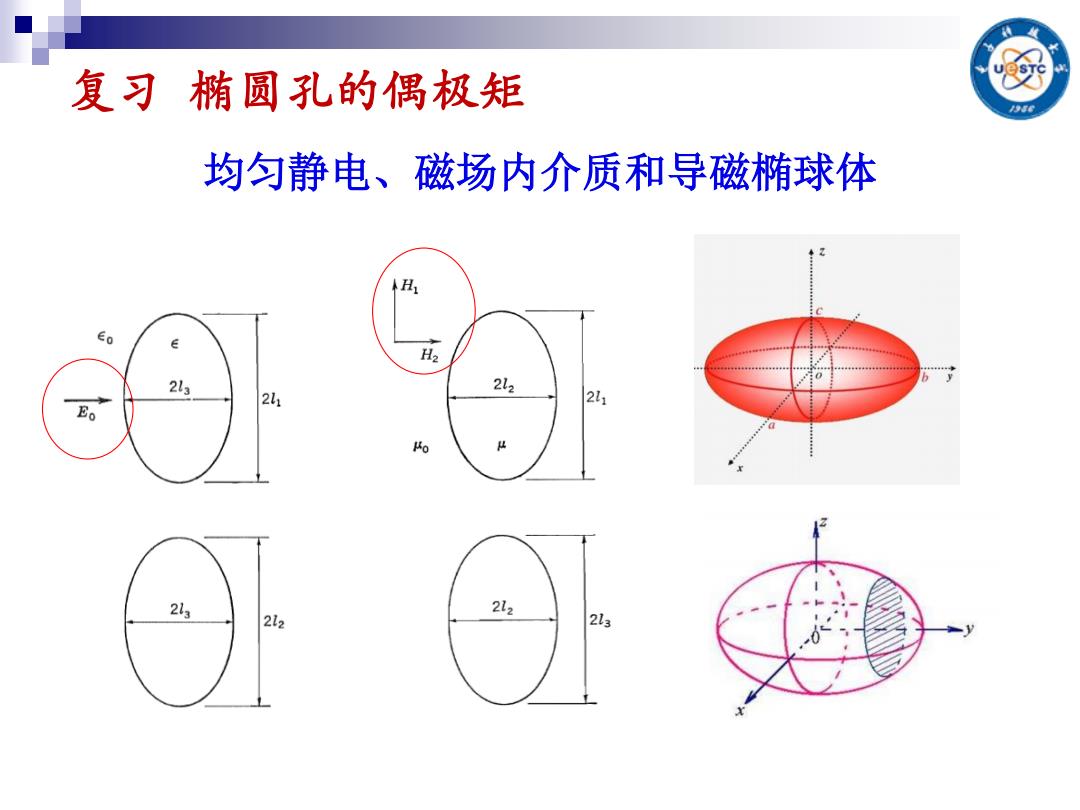
复习椭圆孔的偶极矩 均匀静电、磁场内介质和导磁椭球体 A ∈o H2 2l3 2l2 21 2l1 Eo Ho 23 212 2l2 2L3

复习 椭圆孔的偶极矩 均匀静电、磁场内介质和导磁椭球体