电子科技大学：《高等电磁场理论》课程教学资源（课件讲稿）绪论 Advanced Electromagnetic Field Theory

/958 1 Computational Electromagnetics Laboratory,UESTC 高等电磁场理论 2021年秋季 物理学院计算电磁学及其应用团队 梁锋副教授/熊江副教授

1 Computational Electromagnetics Laboratory, UESTC 高等电磁场理论 2021年秋季 物理学院 计算电磁学及其应用团队 梁锋 副教授 / 熊江 副教授

课程基本信息 1956 Computational Electromagnetics Laboratory,UESTC 1.学时及教学形式：50学时课堂教学 2.:R.F.Harrington,Time-Harmonic Electromagnetic Fields,IEEE Press, 2001等。 3.考核方式：最终考核成绩=平时考核成绩占60%（其中课堂讨 论、考勤、课后作业20%，课堂测验20%，课程设计20%)+期末 考试（按惯例开卷)成绩占40%。 4.先修课程：电磁场与波（或电动力学)、数学物理方程及特殊 函数 5.教学目标：掌握以Maxwell方程组为基础的电磁场理论及解析 计算方法，熟悉典型的电磁波辐射、传播、散射问题的求解

5 Computational Electromagnetics Laboratory, UESTC 1. 学时及教学形式：50学时课堂教学 2. 教材：R. F. Harrington, Time-Harmonic Electromagnetic Fields, IEEE Press, 2001 等。 3. 考核方式：最终考核成绩＝平时考核成绩占60%（其中课堂讨 论、考勤、课后作业20%，课堂测验20%，课程设计20% ） +期末 考试（按惯例开卷）成绩占40% 。 4. 先修课程：电磁场与波（或电动力学）、数学物理方程及特殊 函数 5. 教学目标：掌握以Maxwell方程组为基础的电磁场理论及解析 计算方法，熟悉典型的电磁波辐射、传播、散射问题的求解。 课程基本信息

课程基本信息 1956 Computational Electromagnetics Laboratory,UESTC 为什么要学习时谐电磁场？ 什么是时谐电磁场？ 时谐电磁场：随时间变化关系可写为E(F)e,(单频正弦电磁场) 容易联相到情里叶（递）变换f0-元」P(o)e“d加 E(F.)-2L6(F.0)do 上式说明：随时间任意变化的电磁场均可表示为一系列不同频率 的时谐电磁场的线性叠加。 傅里叶变换（或傅里叶级数）的本质：任意函数均可表示为一系 列不同频率、不同幅度的正弦函数的叠加

6 Computational Electromagnetics Laboratory, UESTC 课程基本信息 为什么要学习时谐电磁场？ 什么是时谐电磁场？ 时谐电磁场：随时间变化关系可写为      j ωt E r e （单频正弦电磁场）     1 2      j ωt f t= F e d     1 , , 2           j ωt E rt= E r e d 上式说明：随时间任意变化的电磁场均可表示为一系列不同频率 的时谐电磁场的线性叠加 。 容易联想到傅里叶（逆）变换 傅里叶变换（或傅里叶级数）的本质：任意函数均可表示为一系 列不同频率、不同幅度的正弦函数的叠加

白光 光著 转镜 ± ab /858 oratory,UESTC signal 非周期信号的梅里叶变换0=25oed恤 周期信号的傅里叶级数s(t)=∑a,em, 2π W0= T 1=-oo 幅值 频率 时 时域分析 频域分析

7 Computational Electromagnetics Laboratory, UESTC 0 0 2 ( ) , jn t n n st ae T w p w ¥ =-¥ = = å 非周期信号的傅里叶变换          s t S e d j t ( ) 2 1 ( ) 周期信号的傅里叶级数 幅值 时域分析 频域分析

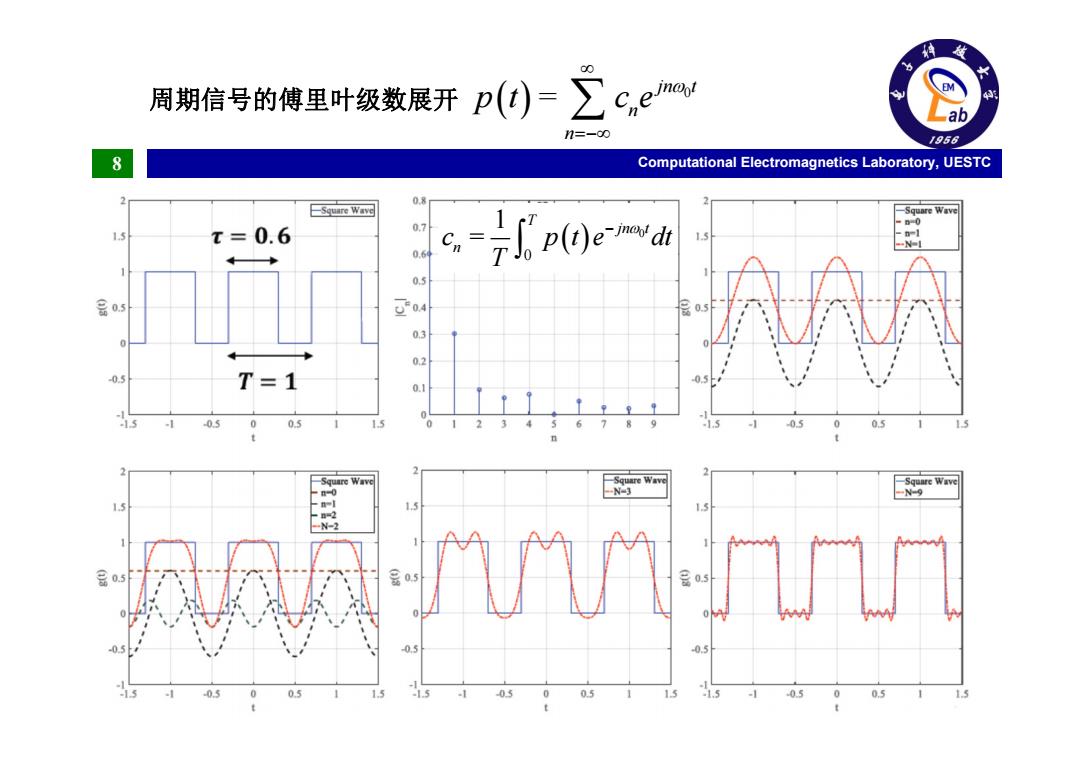
周期信号的傅里叶级数展开 p(t)=∑c,enw ab 1=-oo 1958 8 Computational Electromagnetics Laboratory,UESTC Square Wav四 -Square Wave 1.5 x=0.6 0.7 0.6 Cn= p()emvd -N-I 0.5 品05 4 0.3 0 03 05 T=1 0.1 0. 0 05 1.5 0 0.5 Square Wave Square Wave 0 -N-3 15 1.5 N-2 0.5 0.5 0.5 0.5 -0.5 0.5 1.5 -03 0 0.5 -1.5 0.5 0 0.5 1.5

8 Computational Electromagnetics Laboratory, UESTC   0    jn t n n 周期信号的傅里叶级数展开 p t = ce   0 0 1    T jn t n c = p t e dt T