电子科技大学：《导波场论 Field Theory of Guided Waves》课程教学资源（课件讲稿）第二章 规则波导理论（2/5）

导波场论 第二章规则波导理论(2)

导波场论 第二章 规则波导理论(2)

2.2用位数法求解波导中的场 口由洛伦兹规范 7.A+ 00 0 ▣可得位函数的波动方程 YA-Eu- A or 0 V2φ- 0 口位函数的引入使得我们可以将B和E的求解化为对一个矢量A和一个 标量0的求解，从而使得问题得以简化。而矢量A和标量0又由规范 化条件相联系，所以只需要求出矢量A即可。 导波场论

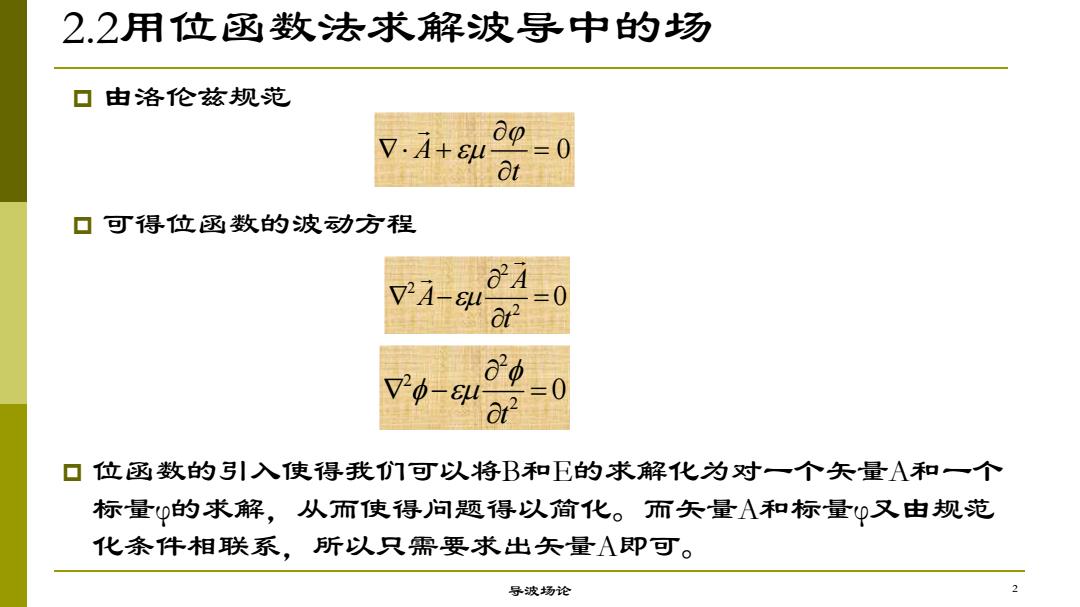
2.2用位函数法求解波导中的场 导波场论 p 由洛伦兹规范 p 可得位函数的波动方程 A 0 t         2 2 2 0 A A t         2 2 2 0 t         p 位函数的引入使得我们可以将B和E的求解化为对一个矢量A和一个 标量φ的求解，从而使得问题得以简化。而矢量A和标量φ又由规范 化条件相联系，所以只需要求出矢量A即可。 2

2.2用位丞数求解波导中的场 口问题：得到了波导中位丞数的亥姆赫兹方程，那么如何简化 求解呢？ ▣解答：通过引入一个新的矢量，赫兹电矢量或者赫兹兹矢量 来解决 导波场论

2.2用位函数求解波导中的场 p 问题：得到了波导中位函数的亥姆赫兹方程，那么如何简化 求解呢？ 导波场论 p 解答：通过引入一个新的矢量，赫兹电矢量或者赫兹磁矢量 来解决 3

2.2用位数求解波导中的扬 口为了使问题进一步简化，引入一个新的矢量赫兹电矢量 A=8L t 口由洛伦滋规范可得： 7·A+ 09 0 0=-7.z 8t 口将赫滋电矢量定义代入滋矢位A的波动方程： 72A- 02A e0 ▣可见赫兹电矢量也满足亥姆赫滋方程 导波场论

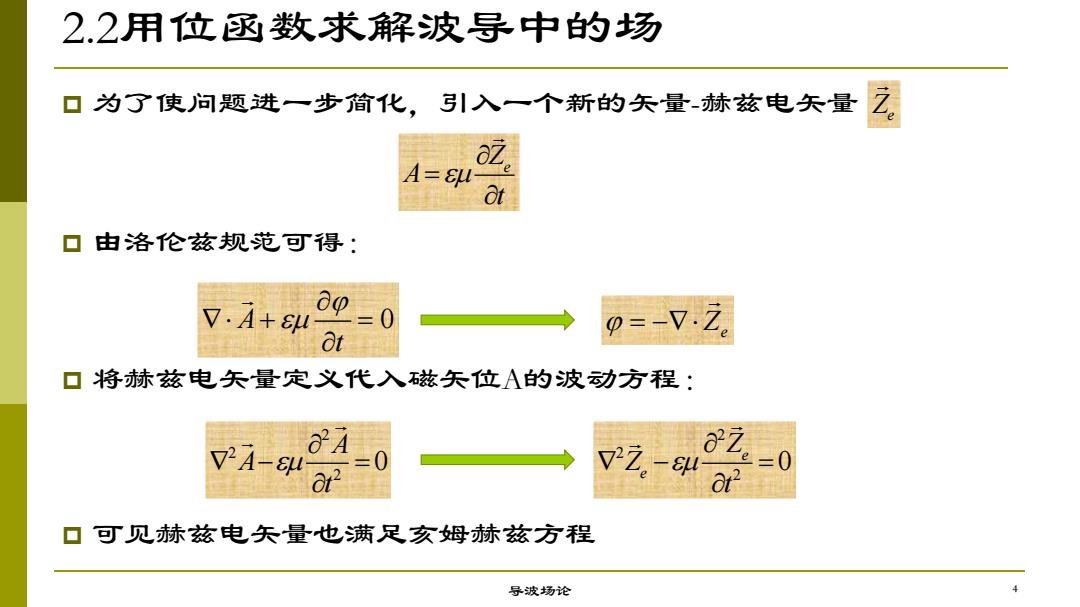
2.2用位函数求解波导中的场 p 为了使问题进一步简化，引入一个新的矢量-赫兹电矢量 导波场论 Ze  Ze A t      p 由洛伦兹规范可得： A 0 t            Z e   p 将赫兹电矢量定义代入磁矢位A的波动方程： 2 2 2 0 A A t         2 2 2 0 e e Z Z t         p 可见赫兹电矢量也满足亥姆赫兹方程 4

2.2用位函数法求解波导中的扬 口设场对时间是简谐变化的，可令： 乙.=1.(2g,)e代> 汽-0→2i+i=0 Z.=I.(p.q.2)e 2 E-- ad voE=K'TI.+V(V.TI.)elm A=卻 0=-7.7 i=lv×A>i=joseVx 口求解电兹场的问题，就化为求解赫兹电矢量的问 题，使问题大大简化。 导波场论

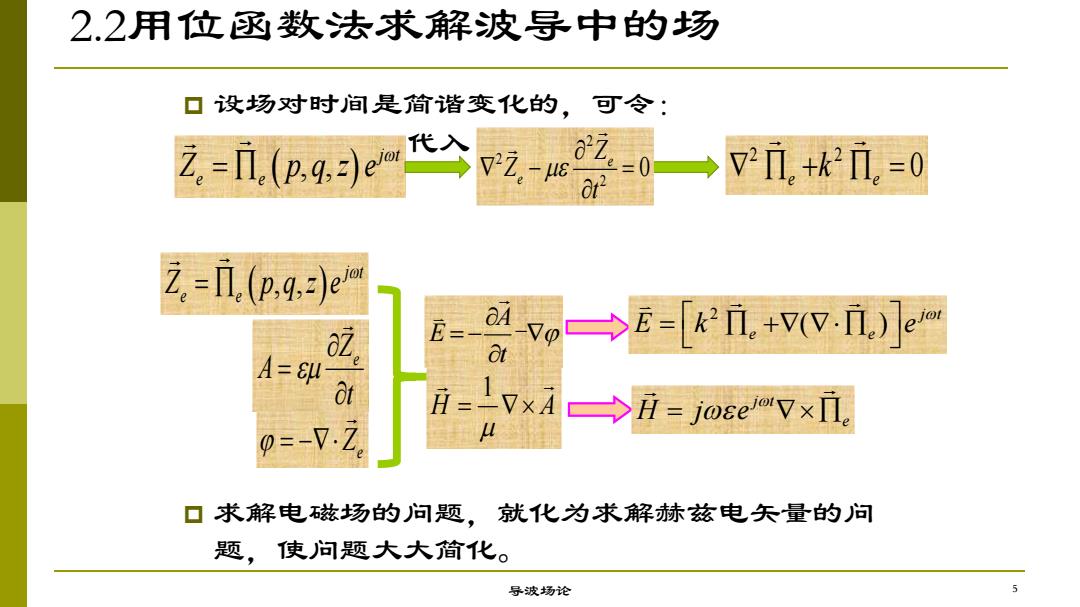
2.2用位函数法求解波导中的场 p 设场对时间是简谐变化的，可令： 导波场论  , ,  j t e e Z p q z e      2 2 2 0 e e Z Z t         2 2 0 e e   k     A E t         - e Z A t      e    Z   , ,  j t e e Z p q z e      2 ( ) j t e e E k e             1 H A      j t e H j e       p 求解电磁场的问题，就化为求解赫兹电矢量的问 题，使问题大大简化。 代入 5