
2.2.1 The allowed values of quantum numbers Quantum Numbers n 0 012012 3 0-10+10-10+1 0-10+1 -2-10+1+2 -2-10+1+2 -3-2-10+1+2+3 n2 9 16
Quantum Numbers n l ml 1 2 3 4 0 0 1 0 1 2 0 1 2 3 0 0 -1 0 +1 0 -1 0 +1 0 -1 0 +1 -2 -1 0 +1 +2 -2 -1 0 +1 +2 -3 -2 -1 0 +1 +2 +3 2.2.1 The allowed values of quantum numbers n2 1 4 9 16

Problem:What values of the azimuthal(1)and magnetic(m)quantum numbers are allowed for a principal quantum number(n)of 4?How many orbitals are allowed for n=4? Plan:We determine the allowable quantum numbers by the rules given in the text. Solution:The values go from 0 to (n-1),and for n=4 they are: 1=0,1,2,3.The values for m go from-/to zero to +l For1=0,m=0 1=1,m1=-1,0,+1 1=2,m=-2,-1,0,+1,+2 1=3,m1=-3,-2,-1,0,+1,+2,+3 There are 16 mL values,so there are 16 orbitals for n=4! as a check,the total number of orbitals for a given value of n is n2,so for n=4 there are 42 or 16 orbitals!
Problem: What values of the azimuthal (l) and magnetic (m) quantum numbers are allowed for a principal quantum number (n) of 4? How many orbitals are allowed for n=4? Plan: We determine the allowable quantum numbers by the rules given in the text. Solution: The l values go from 0 to (n-1), and for n=4 they are: l = 0,1,2,3. The values for m go from -l to zero to +l For l = 0, ml = 0 l = 1, ml = -1, 0, +1 l = 2, ml = -2, -1, 0, +1, +2 l = 3, ml = -3, -2, -1, 0, +1, +2, +3 There are 16 mL values, so there are 16 orbitals for n=4! as a check, the total number of orbitals for a given value of n is n2, so for n = 4 there are 42 or 16 orbitals!

2.2.2 The principal quantum number,n Also called the "energy"quantum number,indicates the approximate distance from the nucleus. Denotes the electron energy shells around the atom, and it is derived directly from the Schrodinger equation. ·The higher the value of“n”,the greater the energy of the orbital. Positive integer values ofn=1,2,3,etc
2.2.2 The principal quantum number, n • Also called the “energy” quantum number, indicates the approximate distance from the nucleus . • Denotes the electron energy shells around the atom, and it is derived directly from the Schrodinger equation. • The higher the value of “n” , the greater the energy of the orbital. • Positive integer values of n = 1 , 2 , 3 , etc
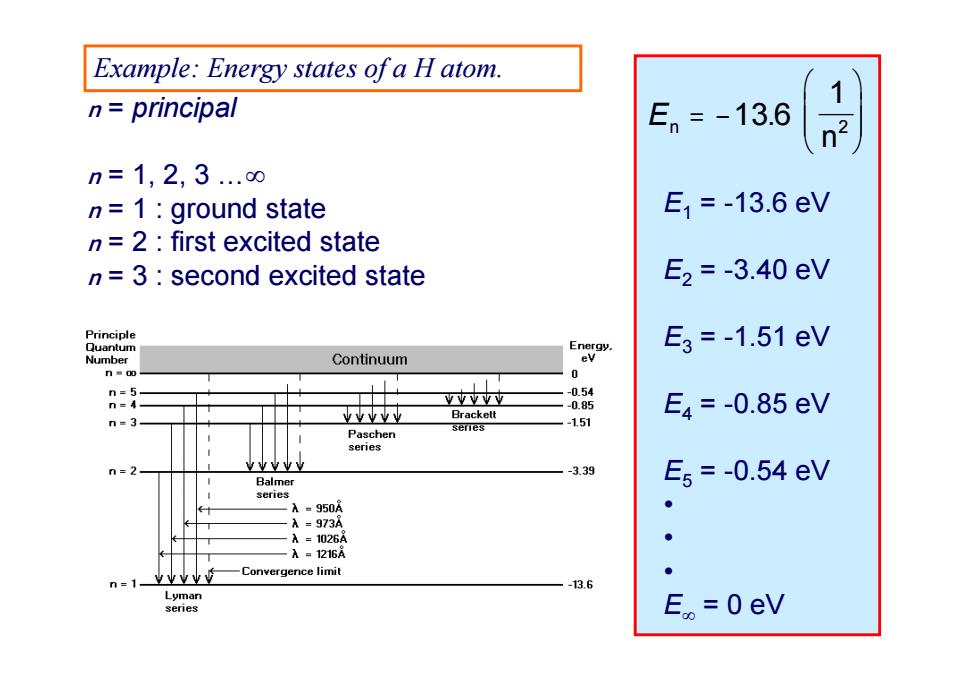
Example:Energy states of a H atom. 1 n=principal En=-13.6 n2 n=1,2,3..0 n=1:ground state E1=-13.6eV n=2:first excited state n=3:second excited state E2=-3.40eV Principle Quantum Energy. E3=-1.51eV Number Continuum ev 0 n=5 n=4 Y业YY7 -0.54 -0.85 E4=-0.85eV n=3 业业业业业 -151 Paschen series Y业V业V n=2 -3.39 Balmer E5=-0.54eV senes -A=950A A=973A A=1026A A=1216A Convergence limit n= Y业业业 -13.6 Lyman senes E。=0eV
n = principal n = 1, 2, 3 … n = 1 : ground state n = 2 : first excited state n = 3 : second excited state En n 13 6 12 . E1 = -13.6 eV E2 = -3.40 eV E3 = -1.51 eV E4 = -0.85 eV E5 = -0.54 eV • • • E = 0 eV Example: Energy states of a H atom
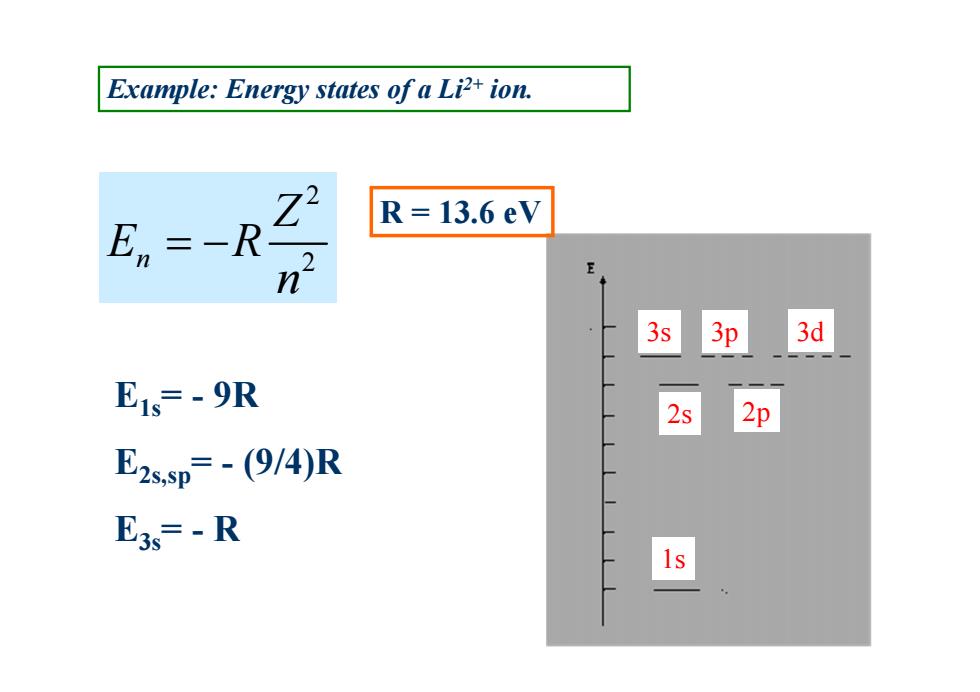
Example:Energy states of a Li2+ion. R=13.6eV E, :-R n 3s 3p 3d E1s=-9R 2s 2p E2s,sp=-(9/4)R E3s=-R
2 n 2 Z E R n R = 13.6 eV Example: Energy states of a Li2+ ion. E1s= - 9R E2s,sp= - (9/4)R E3s= - R 3d 1s 2s 2p 3s 3p