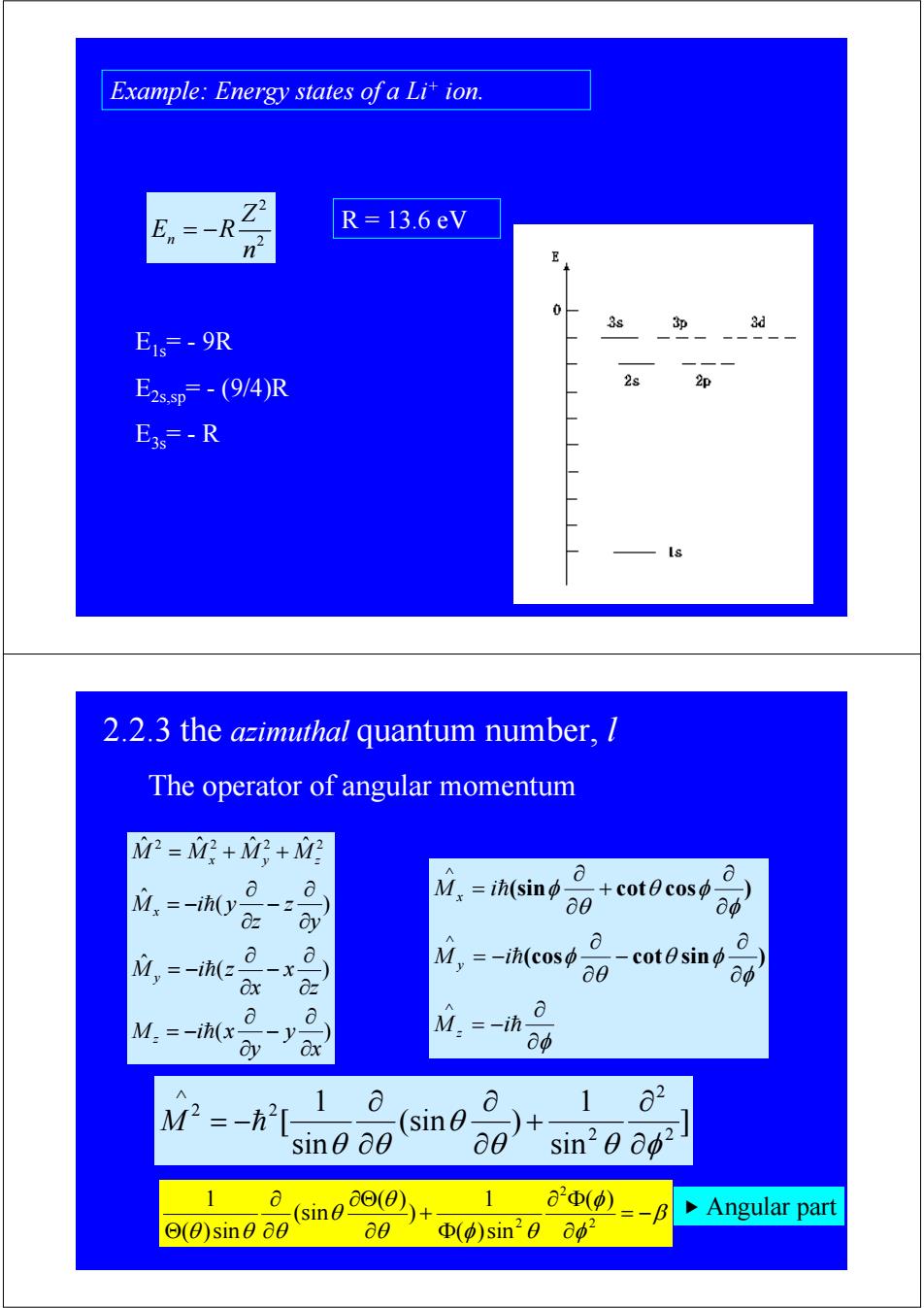
Example:Energy states of a Lit ion. En R=13.6eV n E 0 3s 3印 3d Eis=-9R E2s.p=-(9/4)R 2s 2p E3s=-R 2.2.3 the azimuthal quantum number,l The operator of angular momentum M=M?+Mg+好 M.ih(sino- a +cot0cos 0 M=-ih(y 0 2 dy aφ a M,=-ih(= =-i(cos -一X cotesin Ox 0z a0 8o a a M.=-ih(x点-y M.=-ih- g 中 M2=-h 1 a a 1 o2 sin)+ sine 00 a0 sin20 002 1 a (sin() 1 aΦ(0) =-B Angular part Θ(0)sin0a0 a0 Φ(p)sin20ap2
2 n 2 Z E R n = − R = 13.6 eV Example: Energy states of a Li+ ion. E1s= - 9R E2s,sp= - (9/4)R E3s= - R ( ) ( ) ˆ ( ) ˆ ˆ ˆ ˆ ˆ 2 2 2 2 x y y M i x z x x M i z y z z M i y M M M M z y x x y z ∂ ∂ − ∂ ∂ = − ∂ ∂ − ∂ ∂ = − ∂ ∂ − ∂ ∂ = − = + + h h h The operator of angular momentum φ φ θ φ θ φ φ θ φ θ φ ∂ ∂ = − ∂ ∂ − ∂ ∂ = − ∂ ∂ + ∂ ∂ = ∧ ∧ ∧ h h h M i M i M i z y x (cos cot sin ) (sin cot cos ) ] sin 1 (sin ) sin 1 [ 2 2 2 2 2 θ θ φ θ θ θ ∂ ∂ + ∂ ∂ ∂ ∂ = − ∧ M h 2.2.3 the azimuthal quantum number, l β φ φ θ φ θ θ θ θ θ θ = − ∂ ∂ Φ Φ + ∂ ∂Θ ∂ ∂ Θ 2 2 2 ( ) ( )sin 1 ) ( ) (sin ( )sin 1 f Angular part

M2=-2[ 1 a a 162 (sin sin0 00 a0 sin20002 1 d((sin@, 1 a(2=-B Angular part (0)sin0 a0 a0 Φ()sin0ap2 e(0)t()=-10sn0200+ ⊙(0) a2 sin0 00 in20062 Φ()] ae 1 ={-方2[ 82 (8)sin0a8 (sin Φ()sin20a02 Φ(p)]}Θ(0)Φ(p) 7 2=1(0+1)h2 M2Ψ=22Ψ 2=√10+1)h M=I(I+1)h (1=0,12,3…) Denote the orbital angular momentum. When there exist an angular momentum,there is also a magnetic moment. 2me 4= 2m。 √10+)h=V11+)B。 eh .= =9.274×10-24J.T- Bohr magneton 2m
] sin 1 (sin ) sin 1 [ 2 2 2 2 2 θ θ φ θ θ θ ∂ ∂ + ∂ ∂ ∂ ∂ = − ∧ M h β φ φ θ φ θ θ θ θ θ θ = − ∂ ∂ Φ Φ + ∂ ∂Θ ∂ ∂ Θ 2 2 2 ( ) ( )sin 1 ) ( ) (sin ( )sin 1 f Angular part ( )] sin ( ) (sin ( )) sin ( ) ( ) ( ) [ 2 2 2 2 2 φ θ φ θ θ θ θ θ θ φ θ φ Φ ∂ Θ ∂ Θ + ∂ ∂ ∂ Φ ∂ Θ Φ = − ∧ M h ( )]} ( ) ( ) ( )sin 1 (sin ( )) ( )sin 1 { [ 2 2 2 2 φ θ φ φ θ φ θ θ θ θ θ θ Φ Θ Φ ∂ ∂ Φ Θ + ∂ ∂ ∂ ∂ Θ = −h Ψ = Ψ ∧ 2 2 M λ h h ( 1) ( 1) 2 2 = + = + l l l l λ λ M = l(l +1)h (l = 0,1,2,3⋅⋅⋅) • Denote the orbital angular momentum. When there exist an angular momentum, there is also a magnetic moment. J T Bohr magneton m e l l l l m e M m e e e e e e 24 1 9.274 10 2 ( 1) ( 1) 2 2 − − = = × ⋅ = + = + = − h h β μ β μ

Denote the orbital angular momentum. .Indicates the shape of the orbitals around the nucleus. .Denotes the different energy sublevels within the main level"n" 1=0,1,2..n-1 degeneracy 2/+1 0 1 2 34,5,6.… type p d f g,h,i... degeneracy 3 5 7 9,11,13 一 39 二二日 3石 500 2 2p -1000 个 1500 1S 2.2.4 Magnetic Quantum Number,m Determine the z-component of the orbital angular momentum of the atom. Determine the component u,of the magnetic moment in the direction of the magnetic field M.=-ih(x-y)=-ih 0 oy Ox 88 Ψ=-hΨ=-顶 7 =-ihRO 0o ROb=-iRo 8o 8o -ihR⊙Aimeimo=mhROAem=mhΨ A M.平=mΨ M =mh 八=-m,B
•Indicates the shape of the orbitals around the nucleus. •Denotes the different energy sublevels within the main level “n” degeneracy 1 3 5 7 9, 11, 13 … type l s 0 p 1 d 2 f 3 g, h, i … 4, 5, 6 … l = 0, 1, 2 …n –1 degeneracy = 2 l + 1 Denote the orbital angular momentum. • Determine the z-component of the orbital angular momentum of the atom. • Determine the component μz of the magnetic moment in the direction of the magnetic field. ∂φ ∂ = − ∂ ∂ − ∂ ∂ = − h ih x y y M i x z ( ) ˆ 2.2.4 Magnetic Quantum Number , m M z = m μ z = −mβ e h = − Θ = Θ = Ψ ∂ ∂ = − Θ ∂ ∂Φ ΘΦ = − Θ ∂ ∂ Ψ = − ∂ ∂ Ψ = − ∧ h h h h h h h i R Aime m R Ae m M i i R i R i R Ae im im im z ϕ ϕ ϕ φ φ φ φ Ψ = Ψ ∧ M z mh

2 m=+1 1 m=1 m=0 m=2 m=-1 2 2.2.4 Magnetic Quantum Number,m Denotes the direction or orientation of an orbital m=0,士1,±2..±/ m orbital number of orbitals in a subshell 0 0 =2/+1 0Pz ±1Px ±1 Py 2 0 d2z2x2y2=dz ±1dz 士1 dye ±2 d-y ±2
ml = 0, ±1, ±2 …±l number of orbitals in a subshell = 2 l + 1 ±2 dxy dx2 –y ±2 2 ±1 dyz ±1 0 ±1 ±1 0 0 ml dxz d2z2-x2 -y2 = dz 2 2 py px 1 pz 0 l s orbital 2.2.4 Magnetic Quantum Number , m • Denotes the direction or orientation of an orbital
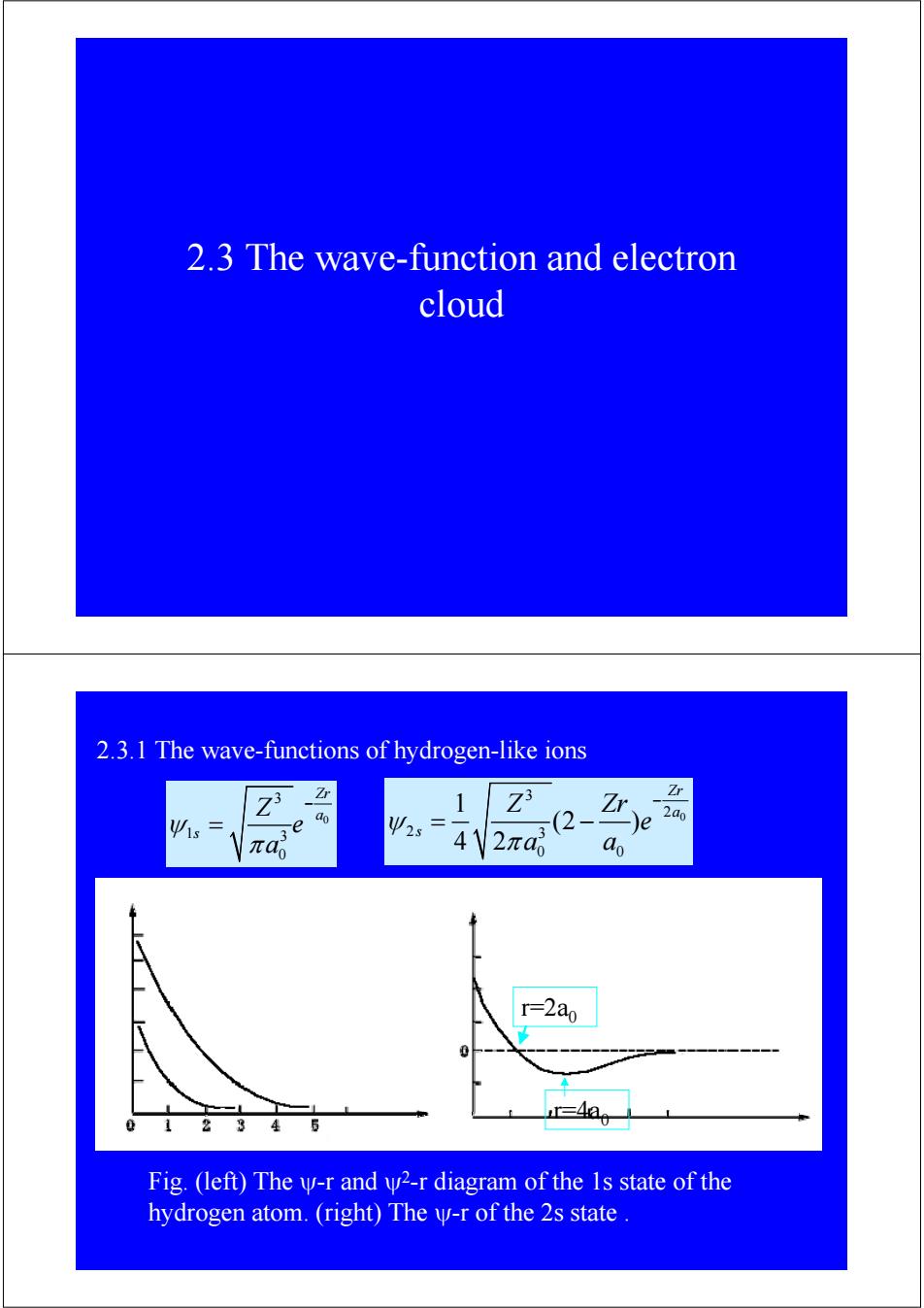
2.3 The wave-function and electron cloud 2.3.1 The wave-functions of hydrogen-like ions 之3 Zr 1 Ψ2= (2- 2a0 41 2π4 ao r=2ao 2345 r=4ao Fig.(left)The y-r and y2-r diagram of the 1s state of the hydrogen atom.(right)The y-r of the 2s state
2.3 The wave-function and electron cloud 2.3.1 The wave-functions of hydrogen-like ions 0 3 1 3 0 Zr a s Z e a ψ π − = 0 3 2 2 3 0 0 1 (2 ) 4 2 Zr a s Z Zr e a a ψ π − = − Fig. (left) The ψ-r and ψ2-r diagram of the 1s state of the hydrogen atom. (right) The ψ-r of the 2s state . r=2a0 r=4a0