电子科技大学：《导波场论 Field Theory of Guided Waves》课程教学资源（课件讲稿）第三章 谐振腔理论（4/5）

复习输入阻抗 根据S0上两端的切向磁场相等，计算出电压电流关系 如腔体只一个输出波导，输出波导只有一个波型 j04 i,*i×乙 4= 1 1 jou a 0 as 9. u U ∑ jou

根据So上两端的切向磁场相等，计算出电压电流关系 = 2 2 1 1 1 1 1 , + 1 1 t a a b t z o a b a a as a E I I H i U Z j j Q Q                                  1 1 1 t t z o E H i I Z   2 2 1 1 1 1 1 1 a a b a b a a as a I I I Y U j j Q Q                      复习 输入阻抗 2 2 1 1 1 1 , + 1 1 a a b a b a a as a I I I U j j Q Q                                 如腔体只一个输出波导，输出波导只有一个波型

复习模式函数的求解 有旋模式： VEn+kEn=0 V×Ea=ki。 Vi。+ki。=0V×i。=kaEa → Ea、Ha、Ka Ea及Ha边界条件 V×(j√EE)=o√u(Vui) V×(√ui)=o√u(i√E) E。=jNEE 对应模式V×尼。=ki。 i。=ai 函数规定V×i。=k。E

复习 模式函数的求解 有旋模式： Ea及Ha边界条件 Ea、Ha、Ka 2 2 2 2 + 0 0 a a a a a a E k E H k H      a a a a a a E k H H k E     对应模式 函数规定( ) ( ) ( ) ( ) j E H H j E               a a a a a a E k H H k E     a a E j E H H    

无旋电场模式Fb: Vo=kpFb V20+k20=0 →Φ、Kb、Fb Fb的系数 Φ的边界条件 归一化条件 无旋磁场模式Gb: Vw=k Gp w+kjw =0 -→4、Kb、G6 Gb的系数 Ψ的边界条件 归一化条件

无旋电场模式Fb： Φ的边界条件 Φ、 Kb 、Fb 归一化条件 Fb的系数 无旋磁场模式Gb： Ψ、 Kb 、Gb 归一化条件 Gb的系数 Ψ的边界条件 2 2 0 b b a k F k         2 2 0 b b b k G k        

3.8小孔耦合 电磁波可通过小孔，由一个导波系统耦合到另一导波系 统或谐振腔中 对于线性尺寸小于工作波长的小孔，已证明： 小孔相当于辐射的电偶极子和磁偶极子的组合 其偶极矩分别正比于入射波中法向电场和切向磁场 (电偶极子&法向电场；磁偶极子&切向磁场) 等效电流定理和等效磁流定理

电磁波可通过小孔，由一个导波系统耦合到另一导波系 统或谐振腔中 3.8 小孔耦合 对于线性尺寸小于工作波长的小孔，已证明： 小孔相当于辐射的电偶极子和磁偶极子的组合 其偶极矩分别正比于入射波中法向电场和切向磁场 （电偶极子&法向电场；磁偶极子&切向磁场） 等效电流定理和等效磁流定理

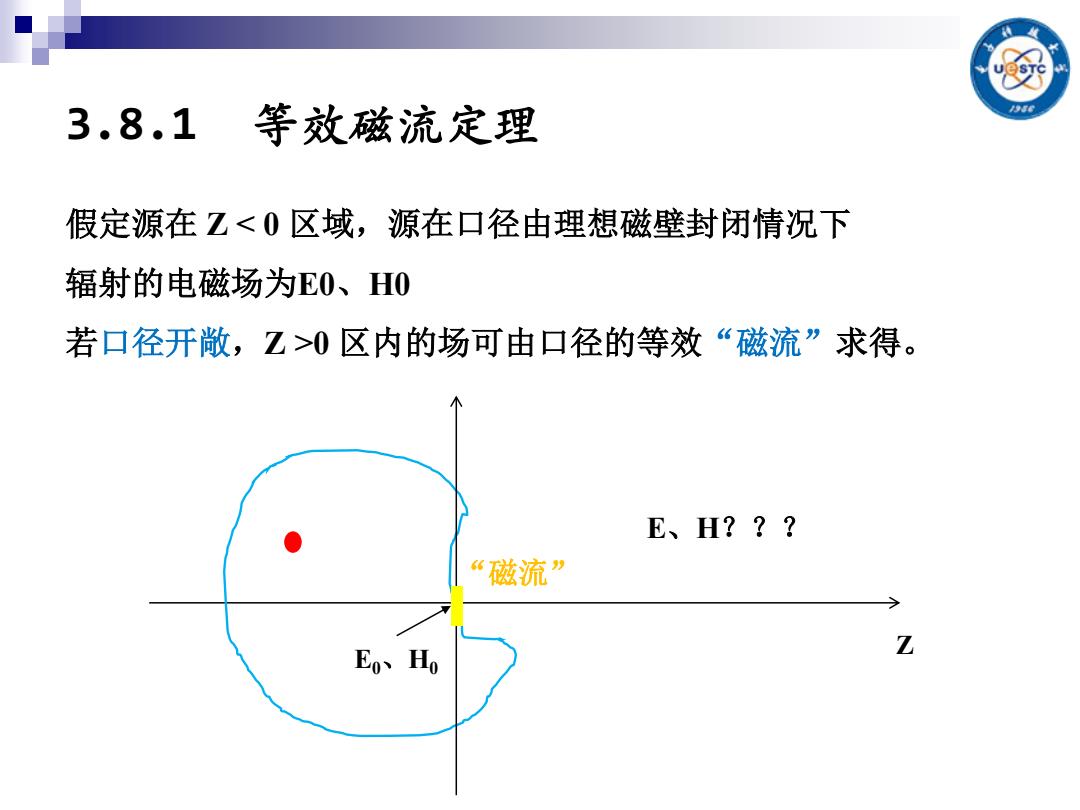
3.8.1 等效磁流定理 假定源在Z<0区域，源在口径由理想磁壁封闭情况下 辐射的电磁场为E0、H0 若口径开敞，Z>0区内的场可由口径的等效“磁流”求得。 E、H??? “磁流” Eo、Ho Z

3.8.1 等效磁流定理 假定源在 Z < 0 区域，源在口径由理想磁壁封闭情况下 辐射的电磁场为E0、H0 若口径开敞，Z >0 区内的场可由口径的等效“磁流”求得。 E0、H0 Z “磁流” E、H？？？