
二.几个重要rv.的期望 1.0-1分布的数学期望 0 Pp 1-p → EX=p 2.二项分布B(n,p) P{X==Cp(1-p)”-R k=0.1,.n )-o
二.几个重要r.v.的期望 1.0-1分布的数学期望 P p − p X 1 1 0 EX=p 2. 二项分布B(n, p) = − − − = n k k n k p p k n k n E X k 1 (1 ) !( )! ! ( ) P X k C p p k n k k n k n { = } = (1− ) = 0.1,. −
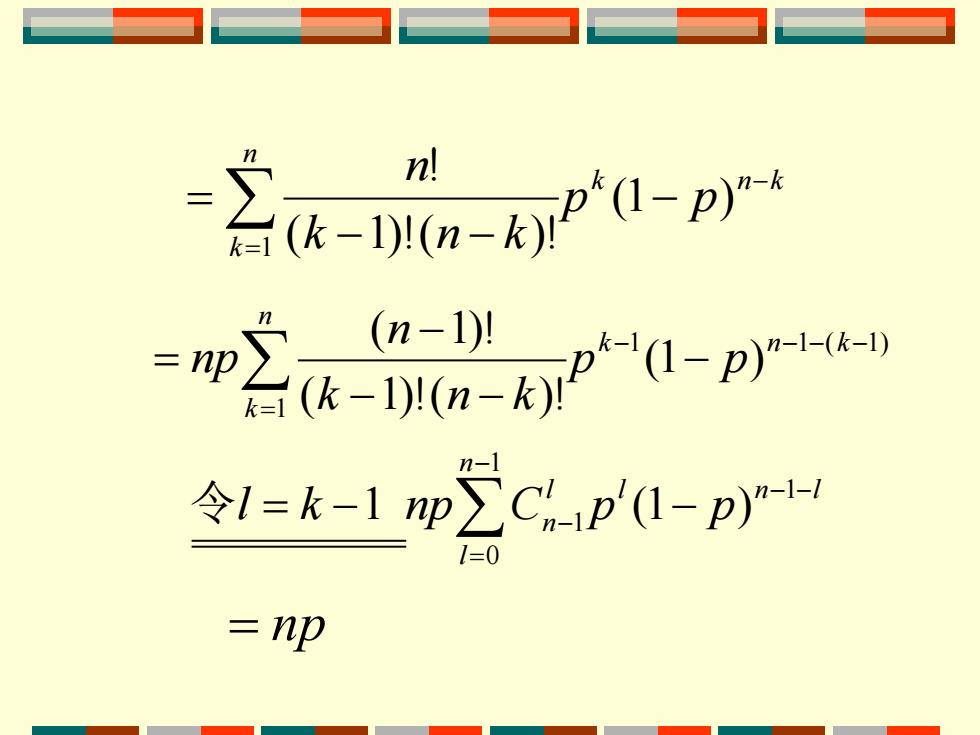
三-内p产 nl =w空a- 令1=k-1p∑Cgp(0-p)H np
k n k n k p p k n k n − = − − − = (1 ) ( 1)!( )! ! 1 1 1 ( 1) 1 (1 ) ( 1)!( )! ( 1)! − − − − = − − − − = k n k n k p p k n k n np= np l n l n l l l k np Cn p p − − − = = − − − 1 1 0 1 令 1 (1 )

3.泊松分布 X-PX=k= 2e,k=0,1,2, n- =, k-0 4.均匀分布U(a,b) 1 &aBa守 a<x<b, 0, 其他 x)-6“生
3.泊松分布 , 0, 1, 2, . ! ~ { = } = = − e k k X P X k k 4. 均匀分布U(a, b) = − 0, , , , 1 ~ ( ) 其他 a x b X f x b a = = − − − = − = = 0 1 1 ; ! ( 1)! ( ) k k k k k e e k E X k + = − = b a a b dx b a x E X ; 2 ( )

5.指数分布 x>0 x≤0 P E(X)=jxie=-jxde和 -xefe
5.指数分布 = − 0 0 0 ( ) x e x f x x 1 = E X x e dx x − = 0 ( ) − = − 0 x xde x e e dx x x − − = − + 0 0

6.正态分布N(,σ) X~f(x)= 1 ,-0<X<0 /2元 -(x-4)2 2o2 dx o =u
6. 正态分布N(, 2 ) − = − − e , x 2 1 X ~ f(x) 2 2 2 (x ) e dx x E X x 2 2 2 ( ) 2 ( ) − − − = ; 2 2 2 e dt x t t t − − − + 令 = =