《光学》课程授课教案（讲义）光的衍射

光学第二章光的衍射 其中A=K三，则心.=+c0m,X-片为数个半被香发出的次该伊省的 r 振幅。其振幅为A:=4A+c0s:),位相因子为(-)-。可见，相邻波带次波的位相相反，且 k越大的波带，振幅越小。于是总的复振幅可表示为 0-8-0.-4+4-4+号4+4-4+号4+4- =4+(-A1 解释：波带数n为奇数，亮点：n为偶数，暗点。 自由传播，n→0，A。→0，A(P)=5A,始终亮点。 圆乐，前个半泼带被遮在，P)-∑1-分A,总是充点。 半波带方程 2-万2=6+k宁2-八2=+专) (1) p2=r2-(,+h)2=r2-r2-2h-h2=k。-2r,h-h2 3 又P2=R2-(R-2=2M-h22h (3) 由（2，（G,2-)2-2h-F2=2M-h 可得h=上-公2 2R+)2R+万2，又由2)式，R*材g-2h 。 所以p=k,R+nR*6 kinskroR 大一公发增奇加起，就瑞装香品 三.一般情形下的波带 如果进一步将每个半波带划分为两个，则相邻波带发出的次波在P点位相差为π2，即第 6

光学 第二章 光的衍射 其中 k i k r S eUKA 0 ~ 2 1   ，则 1 )1)(cos1( ~   k k AU k ) k 1 )1(   k 为第k个半波带发出的次波在P点的复 振幅。其振幅为 ，位相因子为 。可见，相邻波带次波的位相相反，且 k越大的波带，振幅越小。于是总的复振幅可表示为 cos1( k AA       1 21 3 43 5 5 1 1 2 1 () 2 1 2 1 () 2 1 2 1 ( 2 ~ 1 )1()( ~ PU AAAAAAAAU n k k k ])1([ 2 1 1 1 n n A A   解释：波带数n为奇数，亮点；n为偶数，暗点。 自由传播， ， ， n  An  0 1 2 1 )(  APA ，始终亮点。 圆屏，前n个半波带被遮住， 1 1 2 1 )(      n n AAPA ，总是亮点。 半波带方程 0 0 2 0 2 0 2 0 2 ) 2 ) ( 2 ( rk k krrkrrrk    （1） 2 00 2 0 2 0 2 2 0 22 )( 2 2 hhrrkhhrrrhrr  kk k   （2） 又 2 2 2 2  k 2)(  hRhhRR  2Rh （3） 由（2），（3）， 2 0 2 0 2 2 hhrrrk  2 2  hRh 可得  0 )(2)(2 0 0 2 0 2 rR kr rR rr h k      ，又由（2）式， hrrk k 00 2   2 所以    0 0 0 2 0 0 2 rR Rkr rR rk rk k     ) 11( 0 2 Rr k    ，k的奇偶性由r0决定。该式称为半波带方程。 三．一般情形下的波带 如果进一步将每个半波带划分为两个，则相邻波带发出的次波在P点位相差为π/2，即第一 6

光学第二章光的衍射 个半波带中的第一个波带和第二个波带的位相分别为4和34：再将每一个进一步细分，第 个 中的四个波带的位相差为4,位相依此为16,516 可以将任何一个半波带进一步细分为n个，得到更多的波带，相邻波带见光程差为入2n 位相差为h。n很大 ,位相差很小，用振幅矢量法，原来的每个半波带的波矢变为由个小 波矢组成的半圆。如图所示。 四.波带片 用半波带将波面分割，然后只让其中的基数（或偶数）半波带透光，即制成半波带。 半波 相相同，振动方向相同，衍射后大大增强。由于入射光是平面光， 所以 波带片可是做成平面型的 ■■■ 1■■■■ 即满足近轴条件，所以他们 U(P)=A+A+A+.+A。≈10A,P点光强I(P)=100A2,，而自由传播时 U,(P)=)4,光强，(D=子4，相差40倍。可见波带片具有使光汇聚的作用。可以将半 波带方程写成如下形式 R。 长之用装会优人发为 任一波带片，都只适用于一个波长。焦距是固定的。对平行光，波带片为平面的。 但除主焦点之外，还有许多次焦点。 平行光入射，R=有k=PL,即在距离0处，半径为P,的带是第k个半被带。 入r。 当波带片不变时，0改变，会引起k的改变，即可划分的半波带数目改变。 点： r0减小，到ro/4时，k=4k,暗点

光学 第二章 光的衍射 个半波带中的第一个波带和第二个波带的位相分别为π/4和3π/4；再将每一个进一步细分，第 一个半波带中的四个波带的位相差为π/4，位相依此为π/16，5π/16，9π/16，13π/16，.。 可以将任何一个半波带进一步细分为n个，得到更多的波带，相邻波带见光程差为λ/2n， 位相差为π/n。n很大时，位相差很小，用振幅矢量法，原来的每个半波带的波矢变为由n个小 波矢组成的半圆。如图所示。 四．波带片 用半波带将波面分割，然后只让其中的基数（或偶数）半波带透光，即制成半波带。透过 半波带的光，在场点位相相同，振动方向相同，衍射后大大增强。由于入射光是平面光，所以 波带片可是做成平面型的。 一般情况下，可以认为前面几个半波带的倾斜因子相差不大，即满足近轴条件，所以他们 发出的次波的振幅近似相等。如果波带片共有20个半波带，则在P点的复振幅为 531 19 1 )( 10 ~   AAAAAPU ， P 点光强 ，而自由传播时 2  100)( API 1 0 1 2 1 )( ~  APU ，光强 2 0 1 4 1 )(  API ，相差400倍。可见波带片具有使光汇聚的作用。可以将半 波带方程写成如下形式 f k rR k 11 1 2 0    ，同透镜的公式。   k f k 2  为焦距。 任一波带片，都只适用于一个波长。焦距是固定的。对平行光，波带片为平面的。 但除主焦点之外，还有许多次焦点。 R  有 0 2 1 r k k   平行光入射，  ，即在距离r0处，半径为  k 的带是第k个半波带。 当波带片不变时，r0改变，会引起k的改变，即可划分的半波带数目改变。 r0减小，到r0/2时，k=2k，偶数个半波带，暗点； r0减小，到r0/3时，k=3k，其中两两相互抵消，只剩下1/3歌半波带，是亮点，为次焦 点； r0减小，到r0/4时，k=4k，暗点. 7

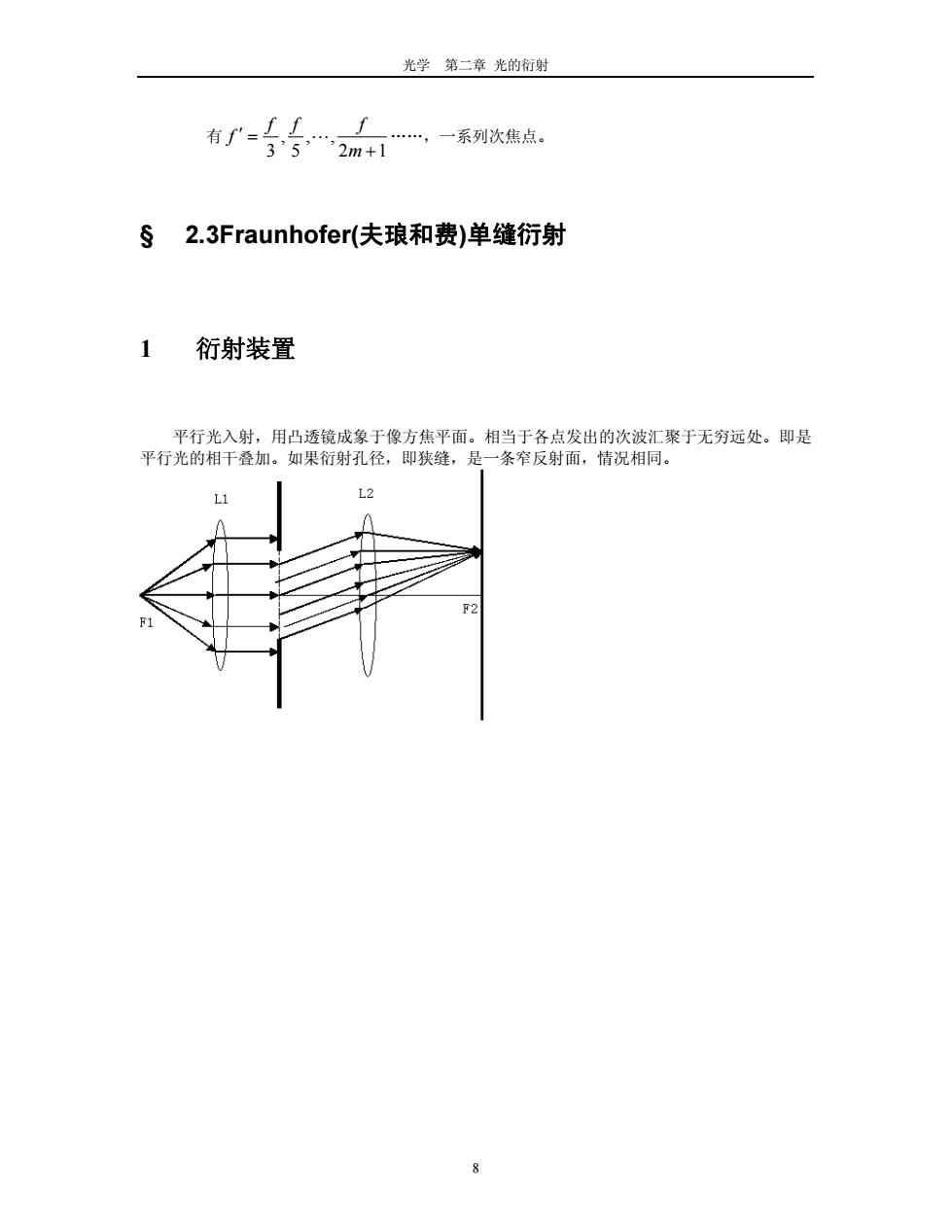
光学第二章光的衍射 有∫二2m+.一系列次焦点， f § 2.3 Fraunhofer(夫琅和费)单缝衍射 1 衍射装置 平行光入射，用凸透镜成象于像方焦平面。相当于各点发出的次波汇聚于无穷远处。即是 平行光的相干叠加。如果衍射孔径，即狭缝，是一条窄反射面，情祝相同。 L1 12

光学 第二章 光的衍射 有 12, 5 , 3    m fff f  .，一系列次焦点。 § 2.3Fraunhofer(夫琅和费)单缝衍射 1 衍射装置 平行光入射，用凸透镜成象于像方焦平面。相当于各点发出的次波汇聚于无穷远处。即是 平行光的相干叠加。如果衍射孔径，即狭缝，是一条窄反射面，情况相同。 8

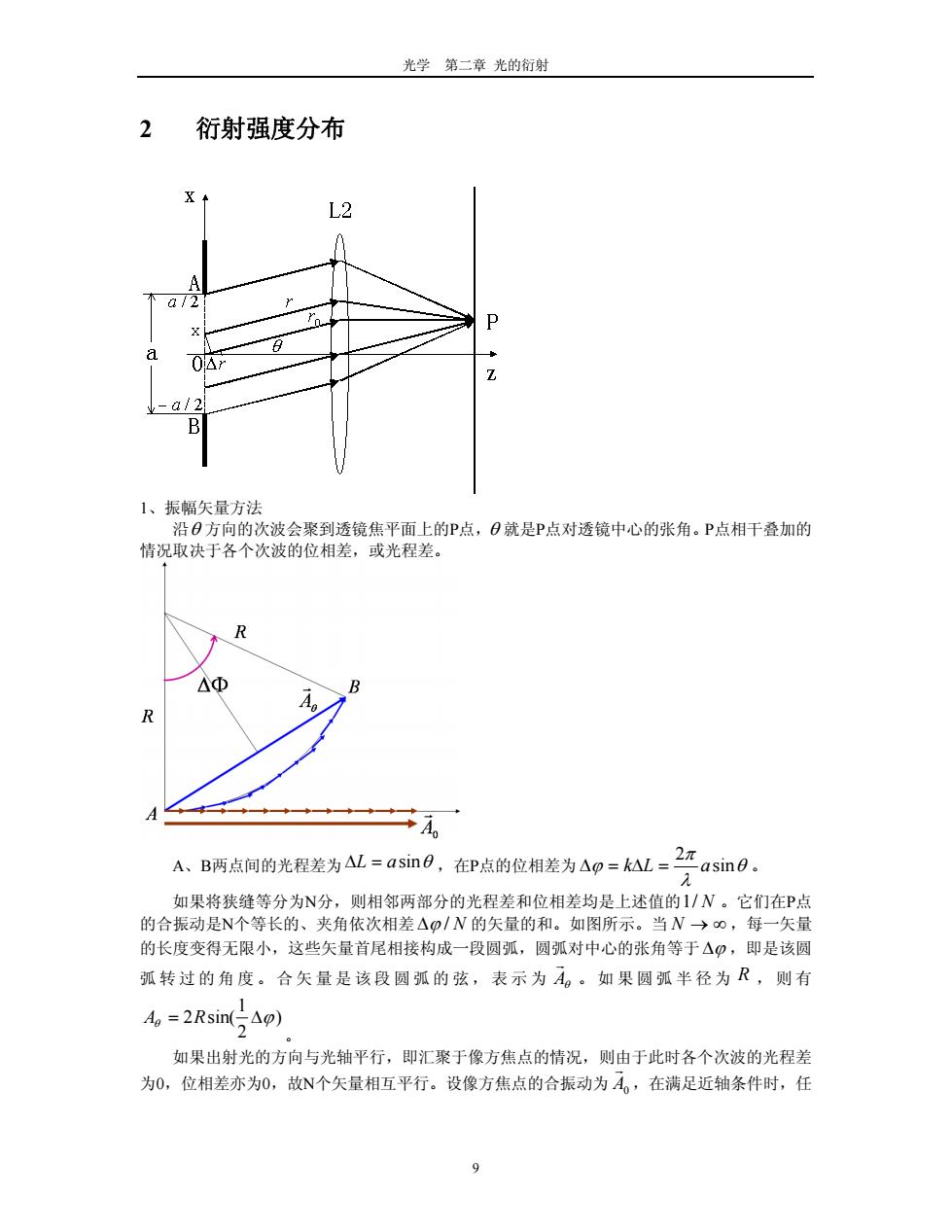
光学第二章光的衍射 衍射强度分布 04 1、振幅矢量方法 方向的次波会聚到透镜焦平面上的P点，0就是P点对透镜中心的张角，P点相干叠加的 情况取于客个次波的位相，或光程老 △D ★A A、B两点间的光程差为△L=asin,在P点的位相差为△p=L=2”asin9 如果将狭缝等分为N分，则相邻两部分的光程差和位相差均是上述值的1/N。它们在P点 的合振动是N个等长的、夹角依次相差△O/N的矢量的和。如图所示。当N→0，每一矢量 的长度变得无限小，这些矢量首尾相接构成一段圆弧，圆弧对中心的张角等于△，即是该圆 弧转过的角度。合矢量是该段圆弧的弦，表示为A。如果圆弧半径为R，则有 ,=2Rsin(5△p) 如果出射光的方向与光轴平行，即汇聚于像方焦点的情况，则由于此时各个次波的光程差 为0，位相差亦为0，故N个矢量相互平行。设像方焦点的合振动为A,在满足近轴条件时，任

光学 第二章 光的衍射 2 衍射强度分布 1、振幅矢量方法 沿 方向的次波会聚到透镜焦平面上的P点， 就是P点对透镜中心的张角。P点相干叠加的 情况取决于各个次波的位相差，或光程差。   aL sin ，在P点的位相差为     sin 2 A、B两点间的光程差为  aLk 。 如果将狭缝等分为N分，则相邻两部分的光程差和位相差均是上述值的 。它们在P点 的合振动是N个等长的、夹角依次相差 N /1 N  / 的矢量的和。如图所示。当  ，每一矢量 的长度变得无限小，这些矢量首尾相接构成一段圆弧，圆弧对中心的张角等于 N   ，即是该圆 弧转过的角度。合矢量是该 弦，表示为 段圆弧的 A  。如果 圆弧半径为 R ，则有 ) 2 。 如果出射光的方向与光轴平行，即汇聚于像方焦点的情况，则由于此时各个次波的光程差 为0，位相差亦为0，故N个矢量相互平行。设像方焦点的合振动为 A0 1   RA sin(2   ，在满足近轴条件时，任 9

光学第二章光的衍射 何一列次波的振幅与其方向无关，即沿任意日方向的次波的振幅与沿光轴方向的次波的振幅相 家则照长份甲降于无，所者名可别 -2Rngp-=2Ap) △p sin(5Ao) =A0 24 4m4 =受n0 光强分布为()=1@)=1，即”。人为像方焦点处的光强. 2、积分方法 P点光来自同一方向，倾斜因子相同。不同方向的光，满足近轴条件，倾斜因子为常数1 即所有F(日，)=1。同时，分母上的r可以视为常数，移到积分号之外 则上式化为 U(P)=K-(Oe=KK=KU() r=r+y,而=-xsin0 etm=K, f -a/ -tnle5-e5吗 -2sn号n0 =K0,@) ae sin(kasin) -iksin =0 sinu 其中，K心，(Q)一e为Q点发出的沿光轴方向的次波在光轴上的F点所引起的复振幅， 0。=Ka二0，(Q)e,为通过整个狭缝的光沿光轴方向传播时在光轴上的F点所引起的振动， 即复。则，=0,0为光上F点处的光强。=如sm0=受sm0,为单缝（单 元)衍射因子。 值得注意的是，表示球面波振幅衰减的因子上中，分母的数值并不能取衍射屏到焦平面的

光学 第二章 光的衍射 何一列次波的振幅与其方向无关，即沿任意 方向的次波的振幅与沿光轴方向的次波的振幅相 等，则弧长 AB 即等于  A0 。所以有   A0 R ，可以得到 ) 2 1 2 sin(  A ) 2 1 sin(2 0     RA    A a a A A sin )sin 2 1 ) 2 1 sin( 0  0  0        sin(   u sin u   其中    sin a u  。 2 2 0 sin 光强分布为 )(  I( ) u u PI   I ， 为像方焦点处的光强。 、积分方法 光来自同一 斜因子为常数1。 即所 0 I 2 P点 方向，倾斜因子相同。不同方向的光，满足近轴条件，倾 有 ),( r F  0   1。同时，分母上的 可以视为常数，移到积分号之外。 则上式化为    r   0 1 ~ 1 )( ~ ikr ikrdx r KdeUKPU ， 2/ 2/ a a e 0 Q)( )( ~ 0  0 QUKK  rrr 0 ，而 r  x sin u u U ka ka ae f Q e UK ( ka i e f K ee ik i f Kdxee f KPU ikr ikr a ik a ik ikr ik ikr ~ sin sin 2 1 )sin 2 1 sin( 1 ) ~ sin )sin 2 2 1 [ ] sin 1 1 )( ~ 0 0 0 sin 2 sin 2 0 sin 0 0 0 0                   其中， ik a a sin( 2/ 2/ 0    0 1 ikr e f )( ~ 0 QUK 为Q点发出的沿光轴方向的次波在光轴上的F点所引起的复振幅， 0 ， * 0 )( ~ 1 ~ 0 0 ikr eQUf  KaU 为通过整个狭缝的光沿光轴方向传播时在光轴上的F点所引起的振动， 为光轴上F点处的光强。    sin sin 2 1 a  kau  ， u sin u 即复振幅。则 0 0 ~ ~  UI U 为单缝（单 元）衍射因子。 值得注意的是， 面波振幅衰减的因子 表示球 r 距离，原因是：各个次波在透镜之前是发散的球面波，但经过透镜的折射，波面改变，成了会 聚的球面波，从理论上讲，由于透镜的孔径总是有限的，所以，当衍射屏距离透镜较远时，通 1 中，分母的数值并不能取衍射屏到焦平面的 10