
定积分 注:若不做代换,就不换限 6xear=6ea-e6=1- x2 2 例5求sin4 xcosxdx 解:sin'xcosxdx=sin4 xdsinx sin5x 1 5 0
例5 求�� 𝝅 𝟐 sin𝟒𝒙𝒄𝒐𝒔𝒙𝒅𝒙 �� :解 𝝅 �� = �𝒅𝒙𝒔𝒐𝒄𝒙𝟒�sin𝟐 𝝅 𝟐 sin𝟒𝒙𝒅𝒔𝒊𝒏𝒙 �� 𝟏 𝒙𝒆 − 𝒙 𝟐 �� =�𝒅� �� 𝟏 𝒆 − 𝒙 𝟐 𝟐 𝒅 𝒙 𝟐 𝟐 = −𝒆 − 𝒙 𝟐 𝟐 | 𝟏 𝟎 = 𝟏 − 𝟏 𝒆 注:若不做代换,就不换限 = ฬ 𝒔𝒊𝒏𝟓𝒙 𝟓 𝝅 𝟐 𝟎 = 𝟏 𝟓

定积分 例4* 求 x2 dx V1-x 解: 设x=sint,则dx=costdt 当x=0 时t=0 x= 1 时t=8 代入原式得: x2 6 dx sin2tdt= 61-c0S2t V1-x dt Jo 2 1π1 π V3 -sin2t 6) 0 12 8
例4* 求 解: 设x = 𝐬𝐢𝐧𝐭 ,则𝒅𝒙 = 𝒄𝒐𝒔𝒕𝒅𝒕 当𝒙 = 𝟎 时𝒕 = 𝟎 𝒙 = 𝟏 𝟐 时𝒕 = 𝝅 𝟔 代入原式得: න 0 1 2 𝑥 2 1 − 𝑥 2 𝑑𝑥 න 0 1 2 𝑥 2 1 − 𝑥 2 𝑑𝑥 = න 0 𝜋 6 𝑠𝑖𝑛 2 𝑡𝑑𝑡 = 1 2 ( 𝜋 6 − ቤ 1 2 𝑠𝑖𝑛2𝑡 𝜋 6 0 ) = 𝜋 12 − 3 8 = න 0 𝜋 6 1 − 𝑐𝑜𝑠2𝑡 2 𝑑𝑡

定积分 例5设f(x)在[-a,a]上连续, 试证明 Erow=fat x为偶数, x为奇数. 证:因为 [rear=心rear+ (1) 对积分∫nf(x)dx做变量代换x=-t, 得心fxdx=-r-0ar=r-a
例5 设𝒇(𝒙) 在[−𝒂, 𝒂] 上连续,试证明 证: 因为 ��−对积分 𝟎 𝒇 𝒙 𝒅𝒙 做变量代换𝒙 = −𝒕, 得 (1) ��− 𝑎 𝑓 𝑥 𝑑𝑥 = ൝ 2 0 𝑎 𝑓 𝑥 𝑑𝑥 𝑥为偶数, 0 𝑥为奇数. න −𝒂 𝟎 𝒇 𝒙 𝒅𝒙 = − න 𝒂 𝟎 𝒇(−𝒕) 𝑑𝑡 = න 0 𝑎 𝑓 −𝑥 𝑑𝑥 න −𝑎 𝑎 𝑓 𝑥 𝑑𝑥 = න −𝑎 0 𝑓 𝑥 𝑑𝑥 + න 0 𝑎 𝑓 𝑥 𝑑𝑥
定积分 当f(x)为偶函数时,f(-x)=f(x), y=f(x) f(x)dx=f(x)dx (1)式变为」af(x)dx=26f(x)dx 当f(x)为奇函数时,f(-x)=-f(x), y=f(x) f(x)dx=-f(x)dx (1)式变为,f(x)dx=0 a 2
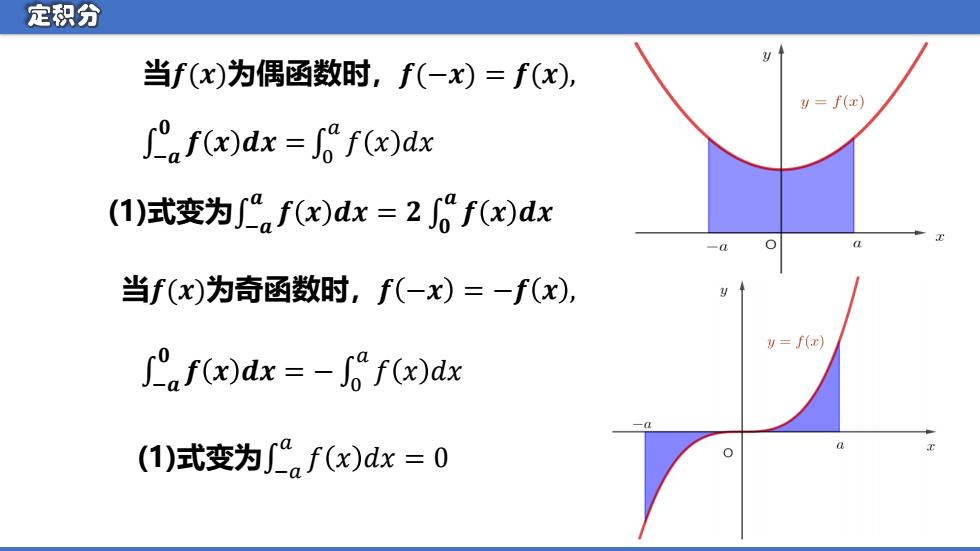
当𝒇(𝒙)为偶函数时,𝒇(−𝒙) = 𝒇(𝒙), ��− 𝟎 0 = �𝒅� �� �� 𝑎 𝑓 𝑥 𝑑𝑥 (1)式变为��− 𝒂 �� �� = �𝒅� �� �� 𝒂 𝒇 𝒙 𝒅𝒙 当𝒇(𝒙)为奇函数时,𝒇 −𝒙 = −𝒇 𝒙 , ��− 𝟎 0 − = �𝒅� �� �� 𝑎 𝑓 𝑥 𝑑𝑥 (1)式变为��− 𝑎 𝑓 𝑥 𝑑𝑥 = 0