
统计学 基本事件(0,0,):试验的每一个结果都是一个事件,这 些事件不可能再分解成更简单的事件 一般的事件由基本事件复合而成。 例如:考察掷一个骰子一次的试验,可能发生的结果有6种 ·“掷得1点” ·“掷得2点” ·“掷得3点” ·“掷得4点” ·“掷得5点” 基本事件 ·“掷得6点 “掷得奇数1 “掷得偶数 复合事件
•基本事件( ):试验的每一个结果都是一个事件,这 些事件不可能再分解成更简单的事件 •一般的事件由基本事件复合而成。 例如:考察掷一个骰子一次的试验,可能发生的结果有6种 • “掷得1点” • “掷得2点” • “掷得3点” • “掷得4点” • “掷得5点” • “掷得6点” • “掷得奇数” • “掷得偶数” 基本事件 复合事件 0 1 ,

统计学 例1对于试验E:将一枚硬币连抛三次,考虑正 反面出现的情况,若记“正面”为H, “反面” 为T, 则基本事件有:HHH,HHT,HTH,THH,HTT, THT,TTH,TTT 随机事件 A=“至少出一个正面” =HHH,HHT,HTH,THH,HTT,THT,TTH; B=“两次出现同一面”三HHH,TTT C=“恰好出现一次正面”=HTT,THT,TTH母
例1 对于试验E: 将一枚硬币连抛三次,考虑正 反面出现的情况,若记“正面”为H, “反面” 为T, 则基本事件有:HHH, HHT, HTH, THH,HTT, THT,TTH , TTT 随机事件 A=“至少出一个正面” ={HHH, HHT, HTH, THH,HTT,THT,TTH}; B=“两次出现同一面”={HHH,TTT} C=“恰好出现一次正面”={HTT,THT,TTH}

三、事件的集合论定义 统计学 20世纪,冯.米泽斯(Von Mises)开始用集合论研究事件。 1.样本空间 。样本点:随机试验E的每一个可能结果 样本空间:样本点的全体,即随机试验的所有可能结果组 成的集合,记为 例1:掷一枚硬币,考察出现向上的面,试验的可能结果有: “正面向上”,“反面向上”两个,则样本空间为: 2={“正面向上”,“反面向上” 若采用记号0一“正面向上”,o,=“反面向上 则2={0,02
◼ 20世纪,冯.米泽斯(Von Mises)开始用集合论研究事件。 1. 样本空间 ◼ 样本点:随机试验E的每一个可能结果 ◼ 样本空间:样本点的全体,即随机试验E的所有可能结果组 成的集合,记为 。 ◼ 例1:掷一枚硬币,考察出现向上的面,试验的可能结果有: “正面向上” , “反面向上”两个,则样本空间为: 三、事件的集合论定义 1 2 2 1 若采用记号 =“正面向上” , =“反面向上” 则 = , =“正面向上” , “反面向上”

统计学 2.事件的集合论定义 000000●■000000■000 事件可以看作是样本空间的子集 符号 集合论解释 概率论解释 2 空间 必然事件、样本空间 空集 不可能事件 ) 点(元素) 基本事件、样本点 A 子集A 事件A 0∈A O是A中的点 事件A发生 0庄A ①不是A中的点 事件A不发生
2. 事件的集合论定义 ◼ 事件可以看作是样本空间的子集 不是A中的点 事件A不发生 是A中的点 事件A发生 A 子集A 事件A 点(元素) 基本事件、样本点 空集 不可能事件 空间 必然事件、样本空间 符号 集合论解释 概率论解释 A A
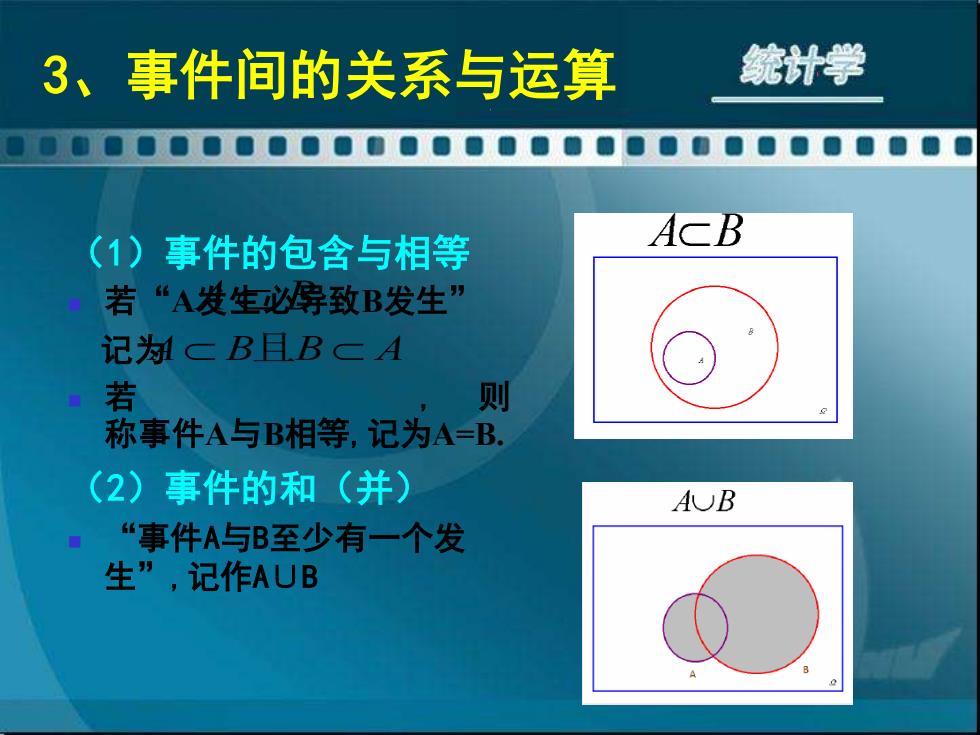
3、事件间的关系与运算 统计学 (1)事件的包含与相等 ACB 若“A发生必碑致B发生” 记为湖三B目B三A 若 则 称事件A与B相等,记为A=B. (2)事件的和(并) AUB “事件A与B至少有一个发 生”,记作AUB
(1)事件的包含与相等 ◼ 若“A发生必导致B发生” 记为 ◼ 若 , 则 称事件A与B相等,记为A=B. (2)事件的和(并) ◼ “事件A与B至少有一个发 生” ,记作A∪B 3、事件间的关系与运算 A B A B B A 且