某化工产品的得率与温度、压力和原料配方有关.为提高得率 下Example 通过试验寻找最佳生产条件.试验因素和水平如下 水平 2 3 4 因素 温度 800 1000 1200 1400 压力 10 20 30 40 配方 A B C D 3个因素,每个因素4个水平共要做43=64次试验.做这么多试验 人力、物力、财力都不可能因此,如何通过尽可能少的试验获得尽 可能多的信息?比如采用正交表安排试验就是一种有效的方法, ⊥Example 如何安排试验方案和分析试验结果,这构成数理统计的另一分支 Previous Next First Last Back Forward 4
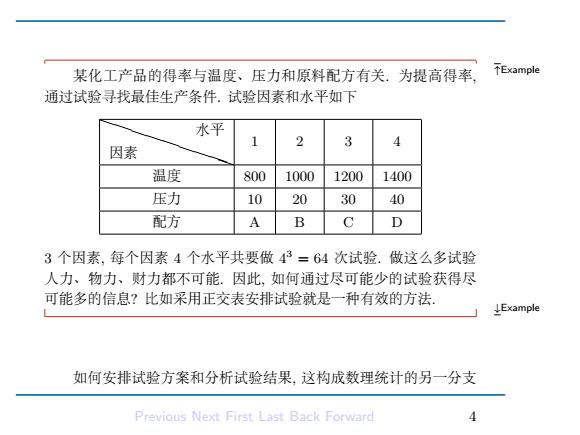
↑Example 某化工产品的得率与温度、压力和原料配方有关. 为提高得率, 通过试验寻找最佳生产条件. 试验因素和水平如下 P 因素 PPPPPPPP 水平 1 2 3 4 温度 800 1000 1200 1400 压力 10 20 30 40 配方 A B C D 3 个因素, 每个因素 4 个水平共要做 4 3 = 64 次试验. 做这么多试验 人力、物力、财力都不可能. 因此, 如何通过尽可能少的试验获得尽 可能多的信息? 比如采用正交表安排试验就是一种有效的方法. ↓Example 如何安排试验方案和分析试验结果, 这构成数理统计的另一分支 Previous Next First Last Back Forward 4

《试验的设计和分析》.在本例中有效收集数据是通过科学安排试 验的方法来实现的 在有效收集数据中一个重要问题是:数据必须具有随机性 2.有效的使用数据 获取数据后,需要用有效的方法,去集中和提取数据中的有关信 息,以对所研究的问题作出一定的结论,在统计上称为“推断” 为了有效的使用数据进行统计推断,需要对数据建立一个统计模 型,并给定某些准则去评判不同统计推断方法的优劣 Previous Next First Last Back Forward 5
—《试验的设计和分析》. 在本例中有效收集数据是通过科学安排试 验的方法来实现的. 在有效收集数据中一个重要问题是: 数据必须具有随机性. 2. 有效的使用数据 获取数据后, 需要用有效的方法, 去集中和提取数据中的有关信 息, 以对所研究的问题作出一定的结论, 在统计上称为 “推断”. 为了有效的使用数据进行统计推断, 需要对数据建立一个统计模 型, 并给定某些准则去评判不同统计推断方法的优劣. Previous Next First Last Back Forward 5

为估计一个物体的重量a,把它在天平上称5次获得数据 下Example x1,x2,·,x5,它们都受到随机性因素的影响(天平的精度反映了 影响的大小).估计a的大小有下列三种不同方法:(1)用5个数的算 术平均值元=(c1+…+x5)去估计a:(2)将x1,x2,…,x5按大 小排列为x≤x2)≤≤x5),取中间一个值r)去估计a(3) 用W=(xa)+x5)去估计a.你可能认为五优于x,而x)优 于W这是不是对的?为什么是这样?在什么条件下才对?事实上 对这些问题的研究正是数理统计学的任务。 ↓Example 要回答这些问题我们需要对数据建立一个统计模型和制定评判不 同统计推断方法的准则.本例中在适当的假定下,可认为数据服从正 态模型 下面我们举一个例子说明采用合适的统计方法也是有效使用数据 的一个重要方面. Previous Next First Last Back Forward 6
↑Example 为估计一个物体的重量 a, 把它在天平上称 5 次获得数据 x1, x2, · · · , x5, 它们都受到随机性因素的影响 (天平的精度反映了 影响的大小). 估计 a 的大小有下列三种不同方法: (1) 用 5 个数的算 术平均值 x¯ = 1 5 (x1 + · · · + x5) 去估计 a; (2) 将 x1, x2, · · · , x5 按大 小排列为 x(1) ≤ x(2) ≤ · · · ≤ x(5) , 取中间一个值 x(3) 去估计 a; (3) 用 W = 1 2 (x(1) + x(5)) 去估计 a. 你可能认为 x¯ 优于 x(3), 而 x(3) 优 于 W. 这是不是对的? 为什么是这样? 在什么条件下才对? 事实上, 对这些问题的研究正是数理统计学的任务. ↓Example 要回答这些问题我们需要对数据建立一个统计模型和制定评判不 同统计推断方法的准则. 本例中在适当的假定下, 可认为数据服从正 态模型. 下面我们举一个例子说明采用合适的统计方法也是有效使用数据 的一个重要方面. Previous Next First Last Back Forward 6

某农村有100户农户,要调查此村农民是否脱贫.脱贫的标准是 TExample 每户年均收入超过1万元.经调查此村90户农户年收入5000元,10 户农户年收入10万元,问此村农民是否脱贫? ↓Example (1)用算术平均值计算该村农户年均收入如下: E=(90×0.5+10×10)/100=1.45(万) 按此方法得出结论:该村农民已脱贫.但90%的农户年均收入只有 5000元,事实上并未脱贫 (2)用样本中位数计算该村农户年均收入:即将100户的年收 入记为x1,x2,…,x100,将其按大小排列为x()≤x(2)≤…≤ x1o0,·样本中位数定义为排在最中间两户的平均值,即 (x(50)+x(51)/2=0.5(万) 按此方法得出结论:该村农民尚未脱贫.这与实际情况相符 Previous Next First Last Back Forward
↑Example 某农村有 100 户农户, 要调查此村农民是否脱贫. 脱贫的标准是 每户年均收入超过 1 万元. 经调查此村 90 户农户年收入 5000 元, 10 户农户年收入 10 万元, 问此村农民是否脱贫? ↓Example (1) 用算术平均值计算该村农户年均收入如下: x¯ = (90 × 0.5 + 10 × 10)/100 = 1.45(万) 按此方法得出结论: 该村农民已脱贫. 但 90% 的农户年均收入只有 5000 元, 事实上并未脱贫. (2) 用样本中位数计算该村农户年均收入: 即将 100 户的年收 入记为 x1, x2, · · · , x100, 将其按大小排列为 x(1) ≤ x(2) ≤ · · · ≤ x(100) . 样本中位数定义为排在最中间两户的平均值, 即 (x(50) + x(51))/2 = 0.5(万) 按此方法得出结论: 该村农民尚未脱贫. 这与实际情况相符. Previous Next First Last Back Forward 7

3. 数理统计方法的归纳性质 数理统计是数学的一个分支,但是它的推理方法是不一样的.统 计方法的本质是归纳式的,而数学则是演绎式的.统计方法的归纳性 质,源于它在作结论时,是根据所观察到的大量的“个别”情况,“归 纳”起来所得.而不是从一些假设、命题或已知事实出发按一定的逻 辑推理得出来的(这后者称为演绎推理).举一例子说明:统计学家 通过大量的观察资料发现,吸烟与某种呼吸系统的疾病有关.他得出 这一结论的根据是:从观察到的大量例子,看到吸烟者中患此种疾病 的比例远高于不吸烟者.他不可能用逻辑推理的方法证明这一点.试 拿统计学与几何学进行比较就可以清楚地看出二者方法的差别所在, 在几何学中要证明“等腰三角形两底角相等”,只需从等腰这个前提出 发,运用几何公理,一步步地推出这个结论(这一方法属于演绎推理)· 而一个习惯于统计方法的人,就可能想出这样的方法:作很多大小形 状不一的等腰三角形,实际测量它的底角查看区别如何,根据所得数 据,看看可否作出底角相等的结论,这属于归纳推理的方法 众所周知,归纳推理是要冒风险的.事实上归纳推理的不确定性 Previous Next First Last Back Forward 8
3. 数理统计方法的归纳性质 数理统计是数学的一个分支, 但是它的推理方法是不一样的. 统 计方法的本质是归纳式的, 而数学则是演绎式的. 统计方法的归纳性 质, 源于它在作结论时, 是根据所观察到的大量的 “个别” 情况, “归 纳” 起来所得. 而不是从一些假设、命题或已知事实出发按一定的逻 辑推理得出来的 (这后者称为演绎推理) . 举一例子说明: 统计学家 通过大量的观察资料发现, 吸烟与某种呼吸系统的疾病有关. 他得出 这一结论的根据是: 从观察到的大量例子, 看到吸烟者中患此种疾病 的比例远高于不吸烟者. 他不可能用逻辑推理的方法证明这一点. 试 拿统计学与几何学进行比较就可以清楚地看出二者方法的差别所在. 在几何学中要证明 “等腰三角形两底角相等”, 只需从等腰这个前提出 发, 运用几何公理, 一步步地推出这个结论 (这一方法属于演绎推理) . 而一个习惯于统计方法的人, 就可能想出这样的方法: 作很多大小形 状不一的等腰三角形, 实际测量它的底角查看区别如何, 根据所得数 据, 看看可否作出底角相等的结论, 这属于归纳推理的方法. 众所周知, 归纳推理是要冒风险的. 事实上归纳推理的不确定性 Previous Next First Last Back Forward 8