
矩形螺纹 按螺纹的牙型分 三角形螺纹 梯形螺纹 锯齿形螺纹 按螺纹的旋向分 了右旋螺纹 左旋螺纹 螺纹的分类 按螺旋线的根数分 单线螺纹 多线螺纹 按回转体的内外表面分 外螺纹 内螺纹 按螺旋的作用分 联接螺纹 传动螺纹 按母体形状分[ 圆柱螺纹 圆锥螺纹
新疆大学专用 作者: 潘存云教授 按螺纹的牙型分 螺纹的分类 按螺纹的旋向分 按螺旋线的根数分 按回转体的内外表面分 按螺旋的作用分 按母体形状分 矩形螺纹 三角形螺纹 梯形螺纹 锯齿形螺纹 右旋螺纹 左旋螺纹 单线螺纹 多线螺纹 外螺纹 内螺纹 联接螺纹 传动螺纹 圆柱螺纹 圆锥螺纹

圆柱螺纹 圆锥螺纹 管螺纹 作者:潘存云教型
新疆大学专用 作者: 潘存云教授 圆柱螺纹 圆锥螺纹 管螺纹
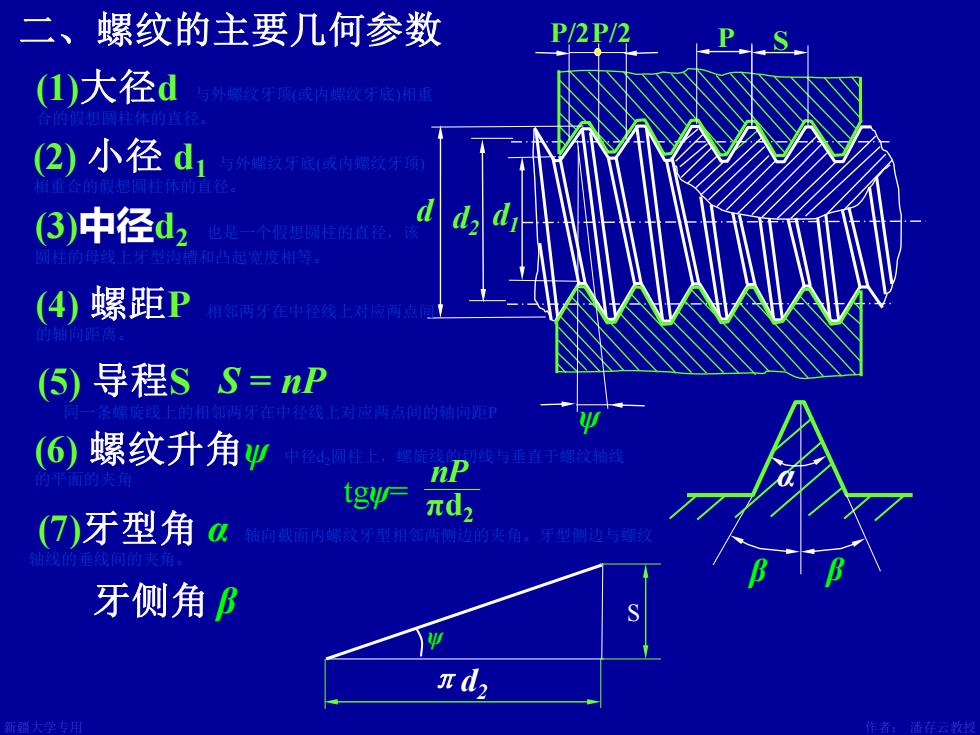
二、螺纹的主要几何参数 P/2P/2 (1)大径d 与外螺纹牙项(或内螺致牙底)相雪 (2)小径d 外螺数牙底或内爆双牙项 (3)中径d2 也是一个假国阿庄的直径 凸起宽度相等 (4)螺距P 相邻两牙在中径线上对应两点 (⑤)导程S S=np 应两点的动而 (6螺纹升角 中径国上 与出螺新线 tgy际 πd (7)牙型角a 轴向喜面内纹牙型相侧边的夹角,牙型侧边与雪 牙侧角B S πd2
新疆大学专用 作者: 潘存云教授 设计:潘存云 (3)中径d2 也是一个假想圆柱的直径,该 圆柱的母线上牙型沟槽和凸起宽度相等。 设计:潘存云 β d2 d1 d (1)大径d 与外螺纹牙顶(或内螺纹牙底)相重 合的假想圆柱体的直径。 (2) 小径 d1 与外螺纹牙底(或内螺纹牙顶) 相重合的假想圆柱体的直径。 (4) 螺距P 相邻两牙在中径线上对应两点间 的轴向距离。 (5) 导程S (6) 螺纹升角ψ 中径d2圆柱上,螺旋线的切线与垂直于螺纹轴线 的平面的夹角 (7)牙型角 α 轴向截面内螺纹牙型相邻两侧边的夹角。牙型侧边与螺纹 轴线的垂线间的夹角。 tgψ= πd2 nP 牙侧角 β α β ψ πd2 S ψ S = nP 同一条螺旋线上的相邻两牙在中径线上对应两点间的轴向距P 二、螺纹的主要几何参数 P/2P/2 P S
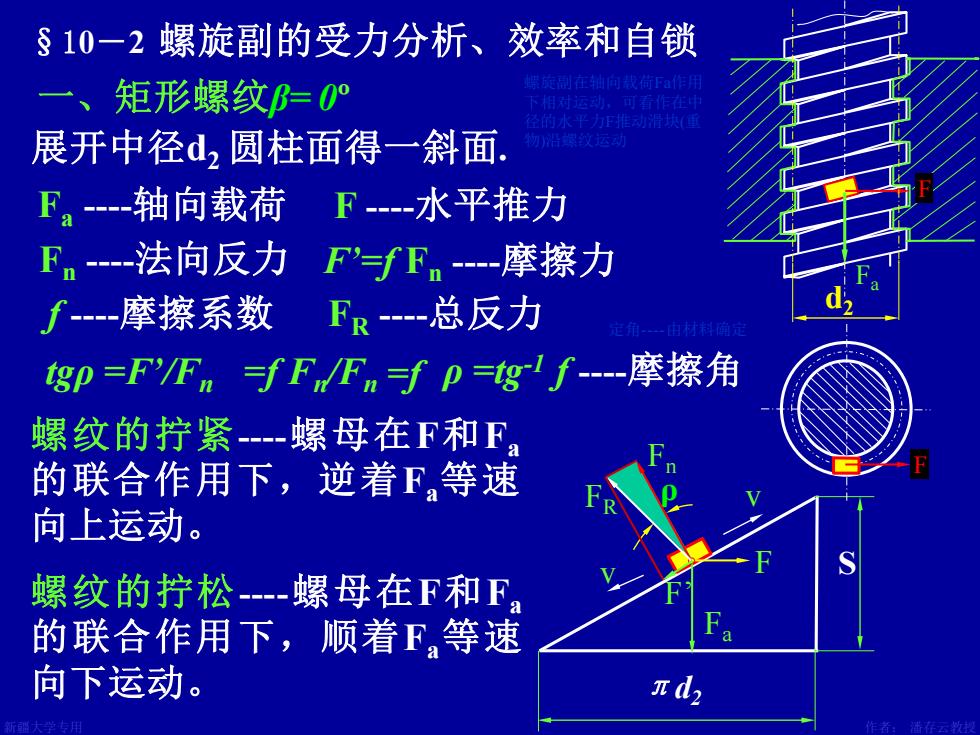
§10一2螺旋副的受力分析、效率和自锁 一、矩形螺纹0° 旋制在荷下a作用 圣的水平力F推动滑执(道 展开中径d,圆柱面得一斜面, 切致运动 Fa-轴向载荷 F-水平推力 F。-法向反力 F'=fFn-摩擦力 f- 摩擦系数 FR-总反力 gp=F'Fn∫F/En=f p=gf-摩擦角 螺纹的拧紧-螺母在F和F。 的联合作用下,逆着F,等速 向上运动。 S 螺纹的拧松-螺母在F和F 的联合作用下,顺着F,等速 向下运动。 πd
新疆大学专用 作者: 潘存云教授 设计:潘存云 v F πd2 S tgρ =F’/Fn F Fa F Fa 螺纹的拧松-螺母在F和Fa 的联合作用下,顺着Fa等速 向下运动。 螺纹的拧紧-螺母在F和Fa 的联合作用下,逆着Fa等速 向上运动。 一、矩形螺纹β= 0º §10-2 螺旋副的受力分析、效率和自锁 展开中径d2 圆柱面得一斜面. 螺旋副在轴向载荷Fa作用 下相对运动,可看作在中 径的水平力F推动滑块(重 物)沿螺纹运动 F -水平推力 Fn -法向反力 Fa -轴向载荷 F’=f Fn -摩擦力 f -摩擦系数 F d2 R -总反力 v ρ =tg-1 =f Fn /Fn =f f -摩擦角 ρ Fn FR 定角-由材料确定 F’
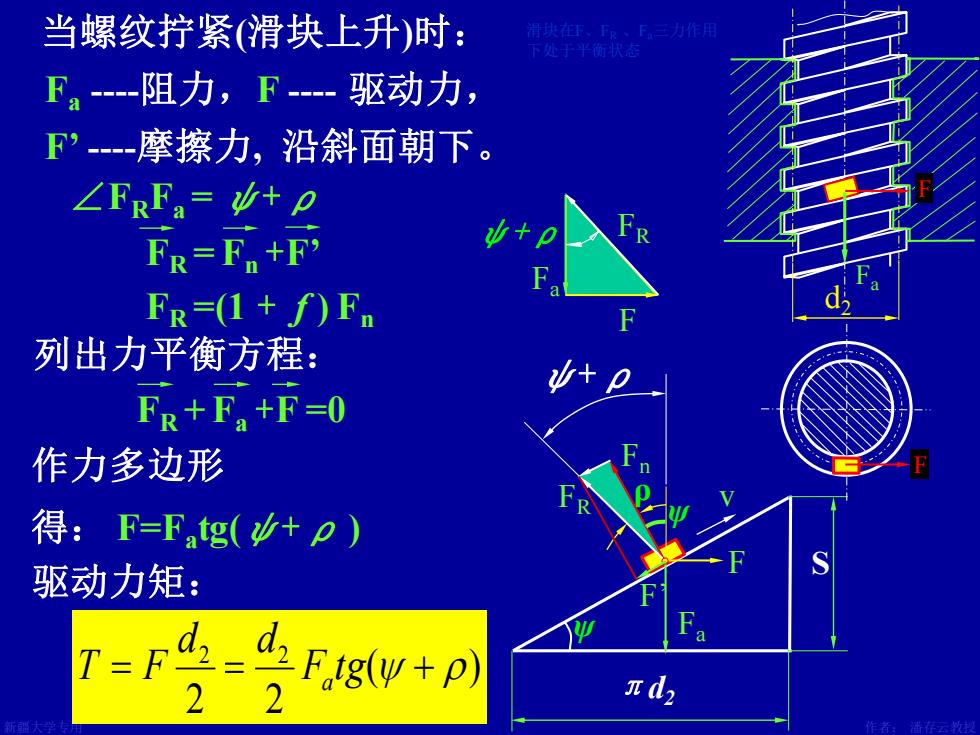
当螺纹拧紧(滑块上升)时: 青块、下、下三力作用 下处于平衡状态 F阻力,F驱动力, F’-摩擦力,沿斜面朝下。 ∠FRFa=+p FR=Fn+F' FR=(1+f)Fn 列出力平衡方程: FR+Fa+F=0 作力多边形 R 得:F=Fg(沙+p) 驱动力矩: S Ftg(w+p) 2 2 πd2
新疆大学专用 作者: 潘存云教授 设计:潘存云 设计:潘存云 ρ ψ+ρ Fn FR v F πd2 S 滑块在F、FR 、Fa三力作用 下处于平衡状态 d2 F Fa F ψ ψ Fa 作力多边形 得: F=Fa tg(ψ+ρ ) 驱动力矩: Fa F FR ( ) 2 2 = F tg + d a 2 2 d T = F 列出力平衡方程: FR + Fa +F =0 ∠FRFa = ψ+ρ FR =(1 + f ) Fn ψ+ρ Fa -阻力,F - 驱动力, 当螺纹拧紧(滑块上升)时: FR = Fn +F’ F’ F’ -摩擦力, 沿斜面朝下