
第7章机械运转速度波动调节 §7一1机械运转速度波动调节的目的和方法 §7-2飞轮的近似设计方法 §7一3飞轮主要尺寸的确定 HIGHER EDUCATION PRESS
新疆大学专用 作者: 潘存云教授 第7章 机械运转速度波动调节 §7-1 机械运转速度波动调节的目的和方法 §7-2 飞轮的近似设计方法 §7-3 飞轮主要尺寸的确定

§7一1机械运转速度波动调节的目的和方法 运动分析时,都假定原动件作匀速运动:o=const 实际上是多个参数的函数:⊙=FP、M、p、m、J 力矩、机构位置、构件质量、转动惯量 研究内容及目的 1.研究在外力作用下机械的真实运动规律,目的是 为运动分析作准备。前迷运动分析曾假定是箭数,但实际上是变化的 2.研究机械运转速度的波动及其调节方法,目的是使 机械的转速在允许范围内波动,而保证正常工作。 设计新的机械,或者分析现有机械的工作性能时 运转的定料 构件的惯件力以及在运动副中产生的反方 的大小、V:,的大小,因此要对机成进行运动分析。而前面所介绍的运动分析时,都假定运动件作匀速运动(三C0nst)。 但在大多数情况下,≠ost,而是力、力矩、机构位置、件质量、转动惯量等参数的函:山三下(P、M、m、) 只有确定了的原动件运动)的变化规律之后 能进行运动分析和力分析,从而为设计新机城提供依据。这就是研究机器运 转的目的
新疆大学专用 作者: 潘存云教授 一、研究内容及目的 1. 研究在外力作用下机械的真实运动规律,目的是 为运动分析作准备。 前述运动分析曾假定是常数,但实际上是变化的 设计新的机械,或者分析现有机械的工作性能时,往往想知道机械运转的稳定性、构件的惯性力以及在运动副中产生的反力 的大小、Vmax amax的大小,因此要对机械进行运动分析。而前面所介绍的运动分析时,都假定运动件作匀速运动(ω=const)。 但在大多数情况下,ω≠const,而是力、力矩、机构位置、构件质量、转动惯量等参数的函数:ω=F(P、M、φ、m、J)。 只有确定了的原动件运动ω的变化规律之后,才能进行运动分析和力分析,从而为设计新机械提供依据。这就是研究机器运 转的目的。 2. 研究机械运转速度的波动及其调节方法,目的是使 机械的转速在允许范围内波动,而保证正常工作。 §7-1 机械运转速度波动调节的目的和方法 运动分析时,都假定原动件作匀速运动:ω=const 实际上是多个参数的函数:ω=F(P、M、φ、m、J) 力、力矩、机构位置、构件质量、转动惯量
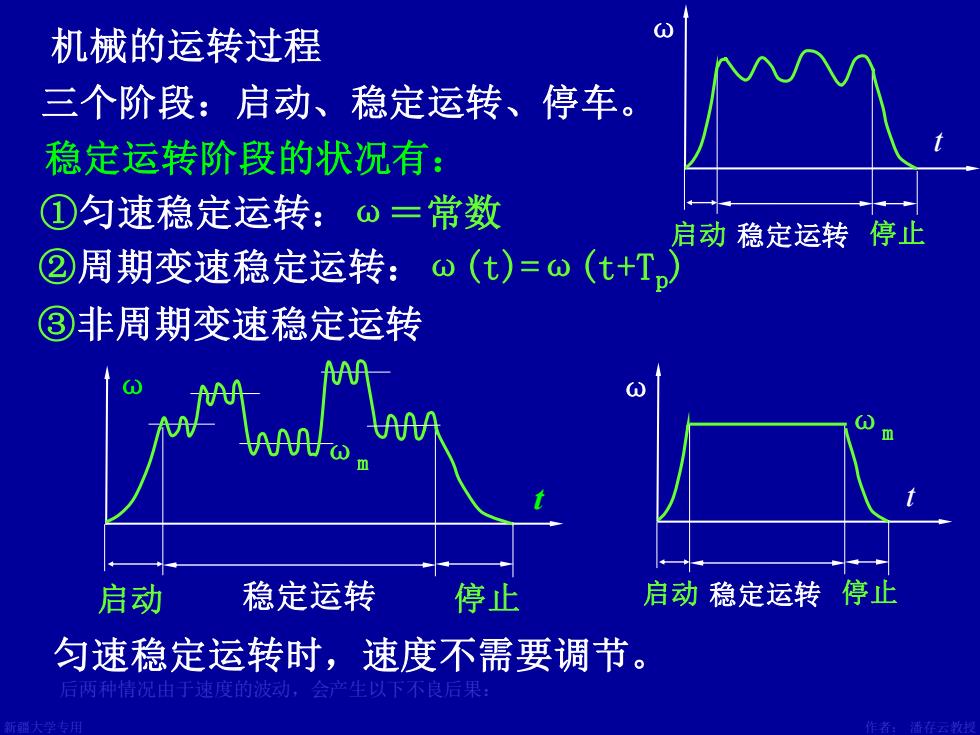
机械的运转过程 三个阶段:启动、稳定运转、停车。 稳定运转阶段的状况有: ①匀速稳定运转:⊙=常数 启动稳定运转停止 ②周期变速稳定运转:o(t)=o(t+T ③非周期变速稳定运转 启动 稳定运转 停止 启动稳定运转停止 匀速稳定运转时,速度不需要调节
新疆大学专用 作者: 潘存云教授 机械的运转过程 稳定运转阶段的状况有: ①匀速稳定运转:ω=常数 稳定运转 ②周期变速稳定运转:ω(t)=ω(t+Tp) 启动 三个阶段:启动、稳定运转、停车。 ③非周期变速稳定运转 t ω 停止 ωm t ω 启动 启动 稳定运转 停止 ωm t ω 稳定运转 停止 匀速稳定运转时,速度不需要调节。 后两种情况由于速度的波动,会产生以下不良后果:

速度波动产生的不良后果: ①在运动副中引起附加动压力,加剧磨损,使工作可 靠性降低。 ②引起弹性振动,消耗能量,使机械效率降低。 ③影响机械的工艺过程,使产品质量下降。 ④载荷突然减小或增大时,发生飞车或停车事故。 为了减小这些不良影响,就必须对速度波动范围进行 调节。 作者:潘存云教型
新疆大学专用 作者: 潘存云教授 速度波动产生的不良后果: ①在运动副中引起附加动压力,加剧磨损,使工作可 靠性降低。 ②引起弹性振动,消耗能量,使机械效率降低。 ③影响机械的工艺过程,使产品质量下降。 ④载荷突然减小或增大时,发生飞车或停车事故。 为了减小这些不良影响,就必须对速度波动范围进行 调节
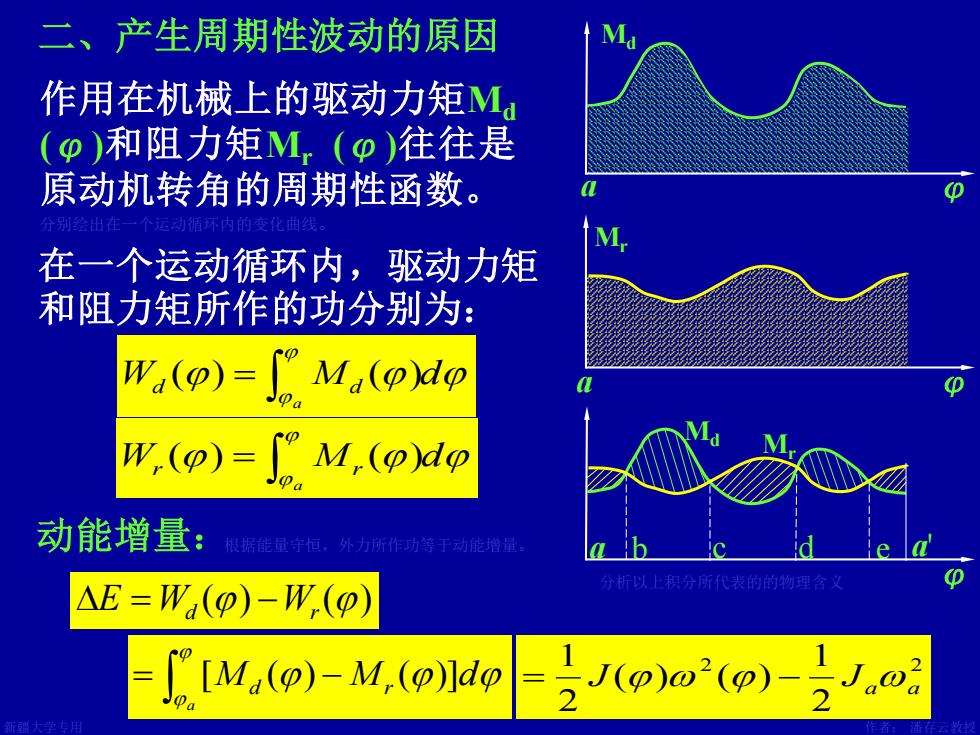
二、产生周期性波动的原因 作用在机械上的驱动力矩M (φ)和阻力矩M(o)往往是 原动机转角的周期性函数。 在一个运动循环内,驱动力矩 和阻力矩所作的功分别为: W.(p)=Ma(pdp 0 W,(p)=["M,(o)dp 动能增量: 根据能量守恒,外力所作动等于动能增量 0 △E=W,(p)-W(p) 分析以上积分所代表的的物理含义 [M.(p)-M.(p)dp-zJ(p)o"(p)-
新疆大学专用 作者: 潘存云教授 二、产生周期性波动的原因 作用在机械上的驱动力矩Md (φ)和阻力矩Mr (φ)往往是 原动机转角的周期性函数。 分别绘出在一个运动循环内的变化曲线。 W M d a d = d ( ) ( ) W M d a r = r ( ) ( ) () () E =Wd −Wr 动能增量: Md Mr a b c d e a' φ = − a [Md ( ) Mr ( )]d 在一个运动循环内,驱动力矩 和阻力矩所作的功分别为: 分析以上积分所代表的的物理含义 2 2 2 1 ( ) ( ) 2 1 = J − J a a 根据能量守恒,外力所作功等于动能增量。 Md a φ Mr a φ