
§15-1单自由度系统的自由振动 力学基础的扩展 单自由度线性系统无阻尼自由振动微分方程 mx +kx-0 这一方程,可以扩展为广义坐标的形式 megq +keag=0 12
12 力学基础的扩展 这一方程,可以扩展为广义坐标的形式 单自由度线性系统无阻尼自由振动微分方程 §15-1 单自由度系统的自由振动 m x + k x=0 meqq + keqq=0

§15-1单自由度系统的自由振动 力学基础的扩展 megq +keg9-O → 9+o.q=0 q-Ccosot+C,cosoi →q=Asin(o,t+0) k 0。 系统的固有频率 q。+ 振动的振幅; m. 0=arctan- 90一振动的初位相;q0一初始广义坐标;90一广义的初始速度。 二、单自由度无阻尼自由振动的特点 1固有频率 (惯性原件)质量m及弹簧刚度(弹性原件)k有关 mg &st 13
13 力学基础的扩展 §15-1 单自由度系统的自由振动 二、单自由度无阻尼自由振动的特点 1 固有频率 (惯性原件)质量m及弹簧刚度(弹性原件)k有关 st g k st k g = = mg k g m k = = 2 0 0 2 q +0 q= q C t C t 1 0 2 0 = cos + cos q A ( t + ) 0 = sin = -系统的固有频率 eq eq 0 m k −振动的振幅; = + 2 0 2 0 0 q A q -振动的初位相; 0-初始广义坐标; 0-广义的初始速度。 0 n 0 arctan q q q q = meqq + keqq=0

§15-1单自由度系统的自由振动 二、单自由度无阻尼自由振动的特点 2振幅与初相位 是两个与初始条件有关的物理量 根据数学运算 振动的振幅; arctan @n9o 振动的初位相;90一初始广义坐标;90一广义的初始速店 90 3 振动规律为简谐振动 q-Asin(@,1+0)
14 §15-1 单自由度系统的自由振动 二、单自由度无阻尼自由振动的特点 2 振幅与初相位 是两个与初始条件有关的物理量 根据数学运算 −振动的振幅; = + 2 0 2 0 0 q A q -振动的初位相; 0 -初始广义坐标; 0 -广义的初始速度 0 n 0 arctan q q q q = 3 振动规律为简谐振动 q A ( t + ) 0 = sin
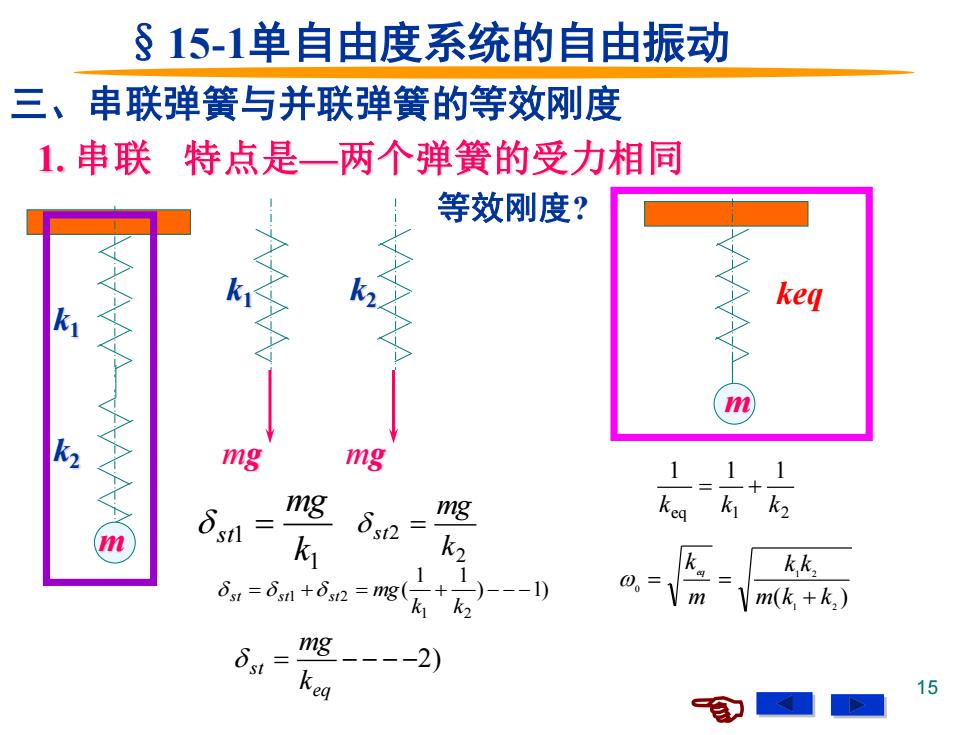
§15-1单自由度系统的自由振动 三、串联弹簧与并联弹簧的等效刚度 1.串联特点是一两个弹簧的受力相同 等效刚度? keq m k2 mg mg 1=1+ mg mg ky k2 m ky δs2 k2 1 kk δ1=δ1+δs2=1g( -1) ky k2 o.-m m(k,+k) mg -2) kea 15
15 §15-1单自由度系统的自由振动 三、串联弹簧与并联弹簧的等效刚度 1. 串联 k1 k2 特点是—两个弹簧的受力相同 mg k1 mg k2 1 1 k mg st = 2 2 k mg st = ) 1) 1 1 ( 1 2 = 1 + 2 = + − − − k k st st st mg = − − − −2) eq st k mg 等效刚度? keq eq 1 2 1 1 1 k k k = + ( ) 1 2 1 2 0 m k k k k m k eq + = = m m

§15-1单自由度系统的自由振动 三、串联弹簧与并联弹簧的等效刚度 2.并联特点是一两个弹簧的变形相同 等效刚度? keq m m mg=keg8st-2) keg =h+k2 mg E=k16F2=k261 m g=F+F2=(k1+k2)δ,t-1) 16
16 §15-1单自由度系统的自由振动 三、串联弹簧与并联弹簧的等效刚度 2. 并联 特点是—两个弹簧的变形相同 st F1 = k1 等效刚度? k1 k2 m k1 k2 m keq m mg F1 F2 st F2 = k2 ( ) 1) mg = F1 + F2 = k1 + k2 st − − − = −− −2) eq st mg k eq 1 2 k = k + k m k k m k eq 1 2 0 + = =