
§15-0 概述 机械振动 1振荡物体的往复运动或状态的循环变化 2振动是一种特殊的振荡。一种运动的物理量时而增 大,时而减少的反复变化 3机械振动工程技术所涉及的机械或结构的振动称作 机械振动 钟摆的往复摆动 汽车行驶时的颠簸机床等工作时的振动 地震时引起的建筑物的振动等 振动的利弊
7 §15-0 概述 一、机械振动 2 振动 是一种特殊的振荡。一种运动的物理量时而增 大,时而减少的反复变化 3 机械振动 工程技术所涉及的机械或结构的振动称作 机械振动 1 振荡 物体的往复运动或状态的循环变化 钟摆的往复摆动 汽车行驶时的颠簸 机床等工作时的振动 地震时引起的建筑物的振动等 振动的利弊

§15-0 概述 一、机械振动 4振动的利弊 振动筛选、振动抛光、振动沉桩 乐器 磨损,减少寿命,影响强度引起噪声等 5学习机械振动的目的 消除或减小有害的振动,充分利用振动为人类服务 二、振动问题的分类 1振动问题所涉及的内容(可以用系统、激励和响应来概括) 机械部件、工程结构等研究对象称为振动系统,简称为系统 初始干扰、强迫力等外界对于系统的作用统称为激励 系统在激励作用下产生的运动称为系统的响应 激励 系统 ◆响应
8 §15-0 概述 一、机械振动 4 振动的利弊 振动筛选、振动抛光、振动沉桩 乐器 磨损,减少寿命,影响强度引起噪声等 消除或减小有害的振动,充分利用振动为人类服务 5 学习机械振动的目的 二、振动问题的分类 1 振动问题所涉及的内容(可以用系统、激励和响应来概括) 机械部件、工程结构等研究对象称为振动系统,简称为系统 初始干扰、强迫力等外界对于系统的作用统称为激励 系统在激励作用下产生的运动称为系统的响应 激励 系统 响应

§15-0 概述 二、振动问题的分类 单自由度系统的振动 按系统的自由度分 多自由度系统的振动 连续体的振动 按激励的有、无和性质分 :固有振动 自由振动 强迫振动 按运动微分方程的形式分 线性振动 非线性振动 9
9 §15-0 概述 二、振动问题的分类 按系统的自由度分 单自由度系统的振动 多自由度系统的振动 连续体的振动 按激励的有、无和性质分 自由振动 固有振动 强迫振动 按运动微分方程的形式分 线性振动 非线性振动
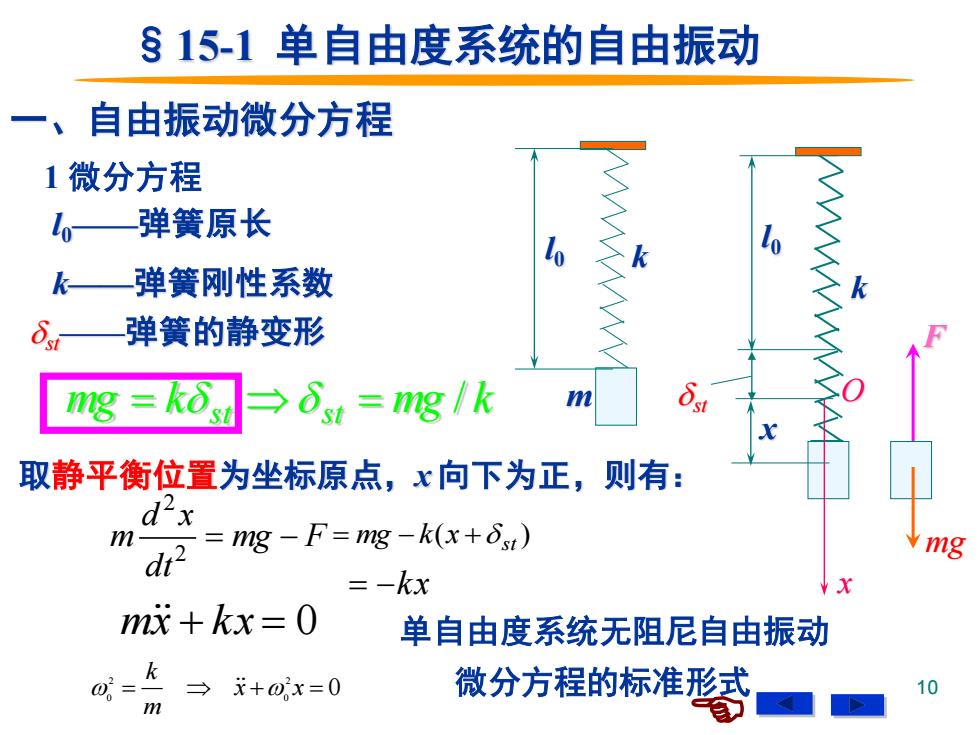
§15-1单自由度系统的自由振动 一、自由振动微分方程 1微分方程 1。—弹簧原长 k—弹簧刚性系数 弹簧的静变形 mg kost →t=1g/k 取静平衡位置为坐标原点,x向下为正,则有: d-x m dt2 =g-F=ng-k(x+δt) mg =-kx mx+kx=0 单自由度系统无阻尼自由振动 @=k →x+0x=0 微分方程的标准形式 10
10 §15-1 单自由度系统的自由振动 l0 m k k x O x l0 F mg 一、自由振动微分方程 l0——弹簧原长 k——弹簧刚性系数 st——弹簧的静变形 mg k mg k st st = = / 取静平衡位置为坐标原点,x 向下为正,则有: ( ) st = mg − k x + = −kx 1 微分方程 单自由度系统无阻尼自由振动 微分方程的标准形式 m x + k x = 0 mg F dt d x m = − 2 2 0 2 0 2 0 = x + x = m k st

§15-1单自由度系统的自由振动 2微分方程的通解 =k三+x=0 m成+kx=0 m x=C coso t+C,sin@t C,C,→积分常数 令:A=VC2+C3,tan0=C,/C2 x=Asin(@t+0) A—振幅 周期T=2π 0—固有频率 0。 1 0,=2π元=2W (o+0) 相位 0—初相位 11
11 A——振幅 0——固有频率 (0 + )——相位 ——初相位 §15-1 单自由度系统的自由振动 2 微分方程的通解 0 2 0 2 0 = x + x = m k m x + k x = 0 x = C1 cos0 t +C2 sin0 t C1 ,C2 积分常数 1 2 2 2 2 1 令: A = C +C , tan = C /C sin( ) x = A 0 t + f T T 2 1 2 2 0 0 = = 周期 =