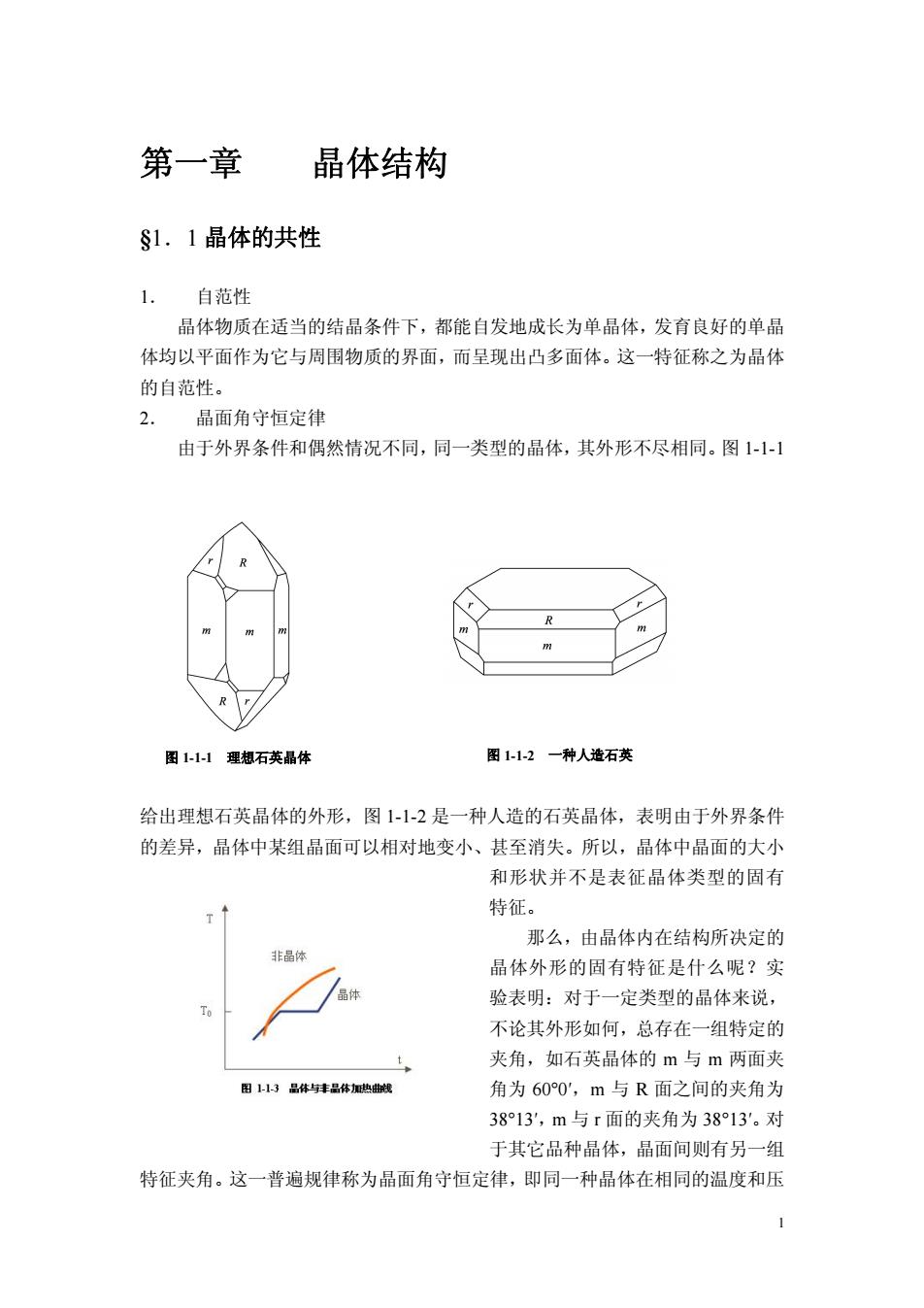
第一章 晶体结构 S1.1晶体的共性 1.自范性 晶体物质在适当的结晶条件下,都能自发地成长为单晶体,发育良好的单晶 体均以平面作为它与周围物质的界面,而呈现出凸多面体。这一特征称之为晶体 的自范性。 2.晶面角守恒定律 由于外界条件和偶然情况不同,同一类型的晶体,其外形不尽相同。图111 图11理想石英晶体 图112一种人适石英 给出理想石英晶体的外形,图1-1-2是一种人造的石英晶体,表明由于外界条件 的差异,晶体中某组晶面可以相对地变小、甚至消失。所以,晶体中晶面的大小 和形状并不是表征品体类型的固有 特征。 那么,由晶体内在结构所决定的 非品 晶体外形的固有特征是什么呢?实 验表明:对于一定类型的晶体来说, 不论其外形如何,总存在一组特定的 夹角,如石英晶体的m与m两面夹 图113品体与芽品体知地线 角为600,m与R面之间的夹角为 3813',m与r面的夹角为3813。对 于其它品种晶体,晶面间则有另一组 特征夹角。这一普遍规律称为晶面角守恒定律,即同一种晶体在相同的温度和压 1
1 第一章 晶体结构 §1.1 晶体的共性 1. 自范性 晶体物质在适当的结晶条件下,都能自发地成长为单晶体,发育良好的单晶 体均以平面作为它与周围物质的界面,而呈现出凸多面体。这一特征称之为晶体 的自范性。 2. 晶面角守恒定律 由于外界条件和偶然情况不同,同一类型的晶体,其外形不尽相同。图 1-1-1 给出理想石英晶体的外形,图 1-1-2 是一种人造的石英晶体,表明由于外界条件 的差异,晶体中某组晶面可以相对地变小、甚至消失。所以,晶体中晶面的大小 和形状并不是表征晶体类型的固有 特征。 那么,由晶体内在结构所决定的 晶体外形的固有特征是什么呢?实 验表明:对于一定类型的晶体来说, 不论其外形如何,总存在一组特定的 夹角,如石英晶体的 m 与 m 两面夹 角为 60°0′,m 与 R 面之间的夹角为 38°13′,m 与 r 面的夹角为 38°13′。对 于其它品种晶体,晶面间则有另一组 特征夹角。这一普遍规律称为晶面角守恒定律,即同一种晶体在相同的温度和压 图 1-1-1 理想石英晶体 图 1-1-2 一种人造石英

力下,其对应晶面之间的夹角恒定不变 3.解理件 当晶体受到敲打、剪切、撞击等外界作用时,可有沿某一个或几个具有确定 方位的晶面劈裂开来的性质。如固体云母(一种硅酸盐刊矿物)很容易沿自然层状 结构平行的方向劈为薄片,晶体的这一性质称为解理性,这些劈裂面则称为解理 面。自然界的品体显露于外表的往往就是一些解理面。 各向异性 晶体的物理性质随观测方向而变化的现象称为各向异性。晶体的很多性质表 现为各向异性,如压电性质、光学性质、磁学性质及热学性质等。例如:石墨的 电导率,当我们沿晶体不同方向测其电导率时,得到方向不同而石墨的电导率数 值也不同的结果。 5. 对称性 晶体的宏观性质一般说来是各向异性的,但并不排斥晶体在某几个特定的方 向可以是异向同性的。晶体的宏观性质在不同方向上有规律重复出现的现象称为 晶体的对称性。 品体的对称性反映在晶体的几何外形和物理性质两个方面。实验表明,晶体 的许多物理性质都与其几何外形的对称性相关
2 力下,其对应晶面之间的夹角恒定不变。 3. 解理性 当晶体受到敲打、剪切、撞击等外界作用时,可有沿某一个或几个具有确定 方位的晶面劈裂开来的性质。如固体云母(一种硅酸盐矿物)很容易沿自然层状 结构平行的方向劈为薄片,晶体的这一性质称为解理性,这些劈裂面则称为解理 面。自然界的晶体显露于外表的往往就是一些解理面。 4. 各向异性 晶体的物理性质随观测方向而变化的现象称为各向异性。晶体的很多性质表 现为各向异性,如压电性质、光学性质、磁学性质及热学性质等。例如:石墨的 电导率,当我们沿晶体不同方向测其电导率时,得到方向不同而石墨的电导率数 值也不同的结果。 5. 对称性 晶体的宏观性质一般说来是各向异性的,但并不排斥晶体在某几个特定的方 向可以是异向同性的。晶体的宏观性质在不同方向上有规律重复出现的现象称为 晶体的对称性。 晶体的对称性反映在晶体的几何外形和物理性质两个方面。实验表明,晶体 的许多物理性质都与其几何外形的对称性相关

S1.2晶体的周期结构描述 1.2.1空间点阵与晶格 (1)空间点阵中点子代表了结构中相同的位置,称为结点。如果晶体是由 完全相同的一种原子所组成,则结点一般代表原子周围相应点的位置,也可能是 原子本身的位置。若晶体是由多种原子组成,通常称这几种原子构成的晶体的基 本结构单元为基元,结点既可以代表基元中任意的点子,也可以代表基元重心。 (2)空间点阵学说准确地描述了品体结构的周期性。由于晶体中所有的基 元完全等价,所以整个晶体的结构可以看做是由基元沿三个不同方向,各按一定 的周期平移而构成的。一般而言,晶体在同一方向上具有相同的周期性,而不同 方向上具有不同周期性。另外,由于结点代表结构中情况相同的位置,因此,任 意两个基元中相应原子周围的情况是相同的,而每个基元中各原子周围的情况则 是不同的。 (3)沿三个不同的方向,通过点阵中的结点可以作许多平行的直线族和平 行的晶面族,使点阵形成三维网格。这些将结点全部包括在其中的网格称为晶格。 由晶格可知,某一方向上相邻两结点之间的距离即是该方向的周期。 (4)结点的总体称为布喇菲点阵,或布喇菲格子。布喇菲格子中,每点周 围的情况都一样。如果晶体由完全相同的一种原子构成,且基元中仅包含一个原 子,则相应的网格就是布喇菲格子,与结点所构成的相同。 布喇菲格子的数学描述: r'=r+14,+1,a2+la(,2,为任意整数) (1-2-1) 去观察所看到的粒子排列在各方向都是一样的。令,2取一切整数,则由式 (11)所确定的空间无穷多个点的集合即定义为一个空间点阵。点阵仅是一个 数学的抽象或者说是一个几何概念。一个实际品体就是由某种原子、分子或其集 团这样的基本结构单元配置在三维点阵上构成的。带有原子、分子或其集团的点 阵就是前面提到的品格。 晶格的基元若只由一个原子构成,原子中心与阵点中心重合,则称为布喇菲 格子,含基元的阵点一般称格点。布喇菲格子的特点是每个原子周围的情况都是 完全一样的。然而,更为普遍的是晶体的基元包括两个或两个以上原子,这种晶 格称为复式格子,复式格子的特点是:各基元中相应的同种原子构成布喇菲格子 且基元中不同原子构成的布喇菲格子是相同的,只是相对地有一定位移。所以复 式格是由若干相同的布喇菲格子相互位移套构而成。 、3
3 §1.2 晶体的周期结构描述 1.2.1 空间点阵与晶格 (1)空间点阵中点子代表了结构中相同的位置,称为结点。如果晶体是由 完全相同的一种原子所组成,则结点一般代表原子周围相应点的位置,也可能是 原子本身的位置。若晶体是由多种原子组成,通常称这几种原子构成的晶体的基 本结构单元为基元,结点既可以代表基元中任意的点子,也可以代表基元重心。 (2)空间点阵学说准确地描述了晶体结构的周期性。由于晶体中所有的基 元完全等价,所以整个晶体的结构可以看做是由基元沿三个不同方向,各按一定 的周期平移而构成的。一般而言,晶体在同一方向上具有相同的周期性,而不同 方向上具有不同周期性。另外,由于结点代表结构中情况相同的位置,因此,任 意两个基元中相应原子周围的情况是相同的,而每个基元中各原子周围的情况则 是不同的。 (3)沿三个不同的方向,通过点阵中的结点可以作许多平行的直线族和平 行的晶面族,使点阵形成三维网格。这些将结点全部包括在其中的网格称为晶格。 由晶格可知,某一方向上相邻两结点之间的距离即是该方向的周期。 (4)结点的总体称为布喇菲点阵,或布喇菲格子。布喇菲格子中,每点周 围的情况都一样。如果晶体由完全相同的一种原子构成,且基元中仅包含一个原 子,则相应的网格就是布喇菲格子,与结点所构成的相同。 布喇菲格子的数学描述: r r a a a l l l l l l 1 1 2 2 3 3 1 2 3 , , 为任意整数 (1-2-1) 去观察所看到的粒子排列在各方向都是一样的。令 l1, l2, l3 取一切整数,则由式 (1-1)所确定的空间无穷多个点的集合即定义为一个空间点阵。点阵仅是一个 数学的抽象或者说是一个几何概念。一个实际晶体就是由某种原子、分子或其集 团这样的基本结构单元配置在三维点阵上构成的。带有原子、分子或其集团的点 阵就是前面提到的晶格。 晶格的基元若只由一个原子构成,原子中心与阵点中心重合,则称为布喇菲 格子,含基元的阵点一般称格点。布喇菲格子的特点是每个原子周围的情况都是 完全一样的。然而,更为普遍的是晶体的基元包括两个或两个以上原子,这种晶 格称为复式格子。复式格子的特点是:各基元中相应的同种原子构成布喇菲格子, 且基元中不同原子构成的布喇菲格子是相同的,只是相对地有一定位移。所以复 式格是由若干相同的布喇菲格子相互位移套构而成

1.2.2原胞与晶胞 点阵和晶格的的概念用于描述晶体微观结构的周期性,从理论上说,无论是 点阵还是晶格都是一个空间的无限图形,研究问题总会有些不便。若取任一格点 ☒ )体心立方 c)立方排(面心立方) 简立方结构 e)体心立方原雕 由面心立方 图1-21立方体系的结构与原胞图示 为顶点,以基矢4,a,4,为边构成平行六面体,整个晶体可看成是由这样的最小 单元在空间以a,4,为周期无限重复排列构成,通常称这样选取的最小的重复 单元为固体物理学原胞或初基原胞,简称原胞。 1.2.3几种典型的晶体结构 1.简立方晶格(c) 原子只分布在边长为a的立方体的8个项角上,原胞和品胞如图1-6所 示。容易知道,这种结构的原胞与晶胞的选取方式是相同的。原子都是仅分布在 立方体的8个顶角上。从整个晶格来看,对于一个晶胞,每个原子为8个晶胞所 共有,平均说来每个品胞包含(8×8=1)一个原子。品胞的体积可以认为是一 个原子所“占据”的体积,这样的晶胞显然也是最小的重复单元,所以对于简立方 4
4 1.2.2 原胞与晶胞 点阵和晶格的的概念用于描述晶体微观结构的周期性,从理论上说,无论是 点阵还是晶格都是一个空间的无限图形,研究问题总会有些不便。若取任一格点 为顶点,以基矢 1 2 3 a a a , , 为边构成平行六面体,整个晶体可看成是由这样的最小 单元在空间以 1 2 3 a a a , , 为周期无限重复排列构成,通常称这样选取的最小的重复 单元为固体物理学原胞或初基原胞,简称原胞。 1.2.3 几种典型的晶体结构 1.简立方晶格(sc) 原子只分布在边长为 a 的立方体的 8 个顶角上,原胞和晶胞如图 1-6 所 示。容易知道,这种结构的原胞与晶胞的选取方式是相同的。原子都是仅分布在 立方体的 8 个顶角上。从整个晶格来看,对于一个晶胞,每个原子为 8 个晶胞所 共有,平均说来每个晶胞包含( 1 8 1 8 )一个原子。晶胞的体积可以认为是一 个原子所“占据”的体积,这样的晶胞显然也是最小的重复单元,所以对于简立方 图 1-2-1 立方体系的结构与原胞图示

晶格来说,其晶胞与原胞相同,即a,=a=ai,=b=gj,4,=c=ak(见图1-2-1(a) 和(d)。 2.体心立方品格 体心立方的一个晶胞包含有两个原子,而原胞要求只包含一个基元,因而通 常选取具有下面的原胞基矢 a,=4(-i+j+k) 4=2-j+) 0,=+1-) (1-2-2) 这样取的初基原体积为×4)号·原胞如图121和所不。仅在 原胞项角上置有原子,故每个原胞只包含一个原子。碱金属LiNa,K,Rb.Cs以及 过渡金属a-Fe,Cr,Mo,W等属于体心立方结构。 3.面心立方晶格(cc) 在面心立方的晶胞中,6个面心上的原子和顶角上的原子是等到同的。由于 从整个晶格来看,每个面心上的原子为相邻的两个晶胞所共有,因而只有12是 属于该晶胞,故每个晶胞含有4个原子。而在周体物理学中,原胞的基矢通常这 样选取如图1-2-1(c)和(D所示。 a,=3(j+k) a,=2k+i0 0,=+ (1-2-3) 同理可以算出每个原胞的体积为/4。面心立方晶格实际上是一种密堆积结构。 贵金属Cu,Ag,Au及Pb,Ni,Al等属于面心立方结构。 以上上讨论的是简单晶格结构,下面举几个重要的复式晶格的实例。 4.氯化铯结构
5 晶格来说,其晶胞与原胞相同,即 1 a a i a , 2 a b j a , 3 a c k a (见图 1-2-1(a) 和(d))。 2.体心立方晶格 体心立方的一个晶胞包含有两个原子,而原胞要求只包含一个基元,因而通 常选取具有下面的原胞基矢 ( ) 2 ( ) 2 ( ) 2 a a a 1 2 3 a i j k a i - j k a i j - k . (1-2-2) 这样选取的初基原胞体积为 3 1 2 3 ( ) 2 a a a a 。原胞如图 1-2-1(b)和(e)所示,仅在 原胞顶角上置有原子,故每个原胞只包含一个原子。碱金属 Li,Na,K,Rb,Cs 以及 过渡金属 α-Fe,Cr,Mo,W 等属于体心立方结构。 3.面心立方晶格(fcc) 在面心立方的晶胞中,6 个面心上的原子和顶角上的原子是等到同的。由于 从整个晶格来看,每个面心上的原子为相邻的两个晶胞所共有,因而只有 1/2 是 属于该晶胞,故每个晶胞含有 4 个原子。而在固体物理学中,原胞的基矢通常这 样选取如图 1-2-1(c)和(f)所示。 ( ) 2 ( ) 2 ( ) 2 a a a 1 2 3 a j k a k + i a i j . (1-2-3) 同理可以算出每个原胞的体积为 3 a / 4。面心立方晶格实际上是一种密堆积结构。 贵金属 Cu,Ag,Au 及 Pb,Ni,Al 等属于面心立方结构。 以上上讨论的是简单晶格结构,下面举几个重要的复式晶格的实例。 4.氯化铯结构