《固体物理学》课程授课教案（讲义）紧束缚近似理论研究性教学教案设计

安徽大学固体物理学研究性 示范课程教案 课程名称： 固体物理 授课教师： 吴明在 联系电话： 15955127125 邮 箱： wumz@ustc.edu.cn

1 安徽大学固体物理学研究性 示范课程教案 课程名称： 固体物理 授课教师： 吴明在 联系电话： 15955127125 邮 箱： wumz@ustc.edu.cn

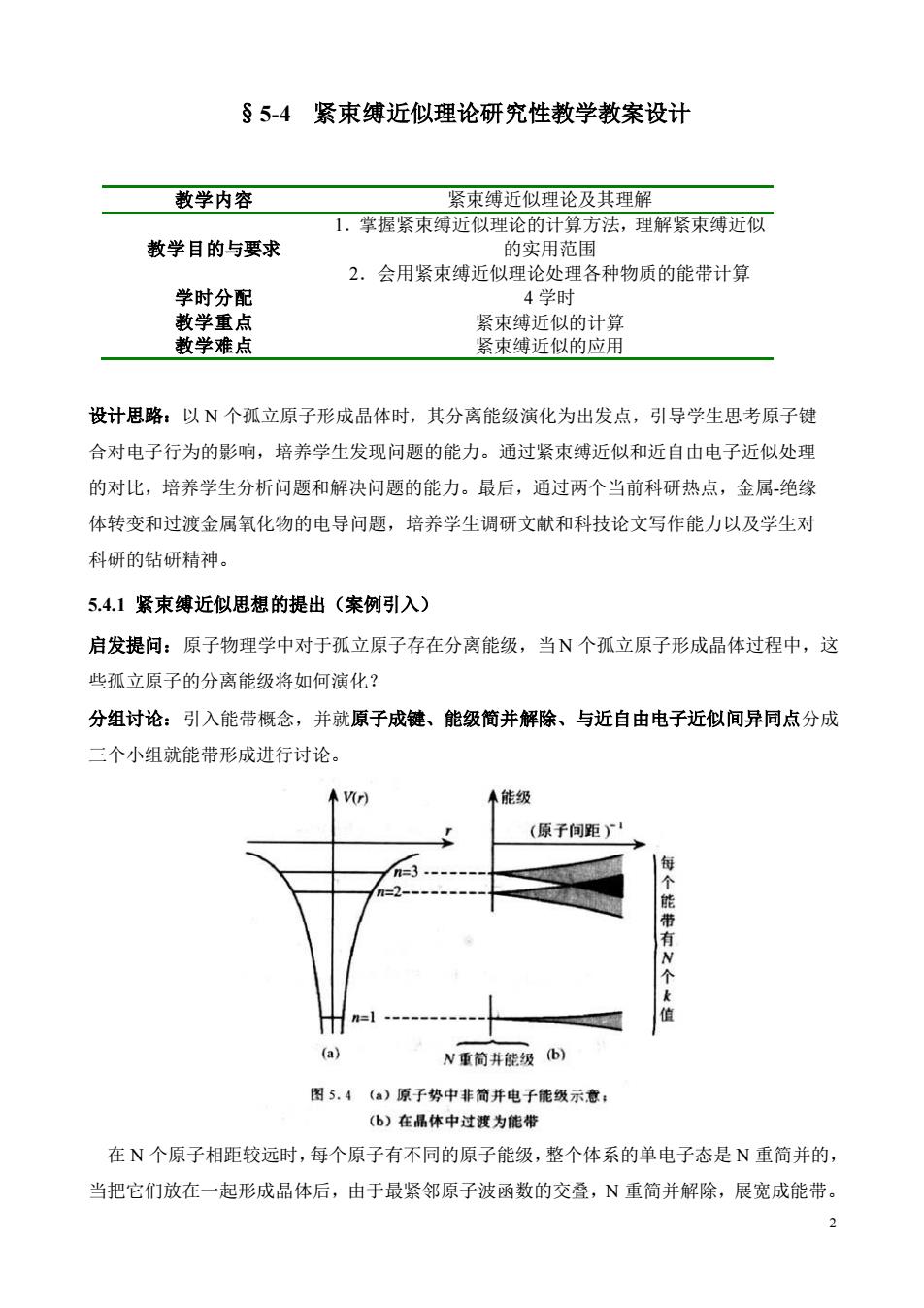
§5-4紧束缚近似理论研究性教学教案设计 教学内容 紧束缚近似理论及其理解 1,掌握紧束缚近似理论的计算方法，理解紧束缚近似 教学目的与要求 的实用范围 学时分配 教学重点 紧束缚近似的计算 教学难点 紧束缚近似的应用 设计思路：以N个孤立原子形成晶体时，其分离能级演化为出发点，引导学生思考原子链 合对电子行为的影响，培养学生发现问题的能力。通过紧束缚近似和近自由电子近似处理 的对比，培养学生分析问题和解决问题的能力。最后，通过两个当前科研热点，金属绝缘 体转变和过渡金属氧化物的电导问题，培养学生调研文献和科技论文写作能力以及学生对 科研的钻研精神。 5.4.1紧束缚近似思想的提出（案例引入） 启发提问：原子物理学中对于孤立原子存在分离能级，当N个孤立原子形成晶体过程中，这 些孤立原子的分离能级将如何演化？ 分组讨论：引入能带概念，并就原子成键、能级简并解除、与近自由电子近似间异同点分成 三个小组就能带形成进行讨论。 能级 (原子间距) 带有N个 (a) N重简并能级b) 图5.4(。)原子势中非简并电子能级示意： (b)在晶体中过渡为能带 在N个原子相距较远时，每个原子有不同的原子能级，整个体系的单电子态是N重简并的， 当把它们放在一起形成晶体后，由于最紧邻原子波函数的交叠，N重简并解除，展宽成能带

2 §5-4 紧束缚近似理论研究性教学教案设计 教学内容 紧束缚近似理论及其理解 教学目的与要求 1．掌握紧束缚近似理论的计算方法，理解紧束缚近似 的实用范围 2．会用紧束缚近似理论处理各种物质的能带计算 学时分配 4 学时 教学重点 紧束缚近似的计算 教学难点 紧束缚近似的应用 设计思路：以 N 个孤立原子形成晶体时，其分离能级演化为出发点，引导学生思考原子键 合对电子行为的影响，培养学生发现问题的能力。通过紧束缚近似和近自由电子近似处理 的对比，培养学生分析问题和解决问题的能力。最后，通过两个当前科研热点，金属-绝缘 体转变和过渡金属氧化物的电导问题，培养学生调研文献和科技论文写作能力以及学生对 科研的钻研精神。 5.4.1 紧束缚近似思想的提出（案例引入） 启发提问：原子物理学中对于孤立原子存在分离能级，当 N 个孤立原子形成晶体过程中，这 些孤立原子的分离能级将如何演化？ 分组讨论：引入能带概念，并就原子成键、能级简并解除、与近自由电子近似间异同点分成 三个小组就能带形成进行讨论。 在 N 个原子相距较远时，每个原子有不同的原子能级，整个体系的单电子态是 N 重简并的， 当把它们放在一起形成晶体后，由于最紧邻原子波函数的交叠，N 重简并解除，展宽成能带

每个能带都包含N个k值。由于能带从原子的能级演化而来，所以内层电子能带常用原子 能级的量子数标记，如3s,3p,3等。若原子所处原子势场的作用较之其它原子势场的作用要 大得多，例如对于原子中内层电子，或品体间距较大时，上面讨论的近自由电子近似就不适 用，这时共有化运动状态与束缚态之间有直接联系，即紧束缚近似理论。 紧束缚理论的实质是把原子间相互作用影响看成微扰的简并微扰方法，微扰后的状态是 N个简并态的线性组合，即用原子轨道，-R,)的线性组合来构成晶体中的电子共有化运动 的轨道(k,r),也称原子轨道线性组合法，简写为LCAO。 教师总结：通过讨论，使学生明白能带的形成只和原子间的结合有关，而和原子间的结合状 态无关，即：能带理论不仅适用于晶体，也适用于非晶体。 5.4.2原子轨道线性组合 问题引入：在上述处理思想的基础上，如何用我们已有的知识点进行表征？ 提示点：1)近自由电子近似能否处理？ 2)如何构筑完备空间表征？ 3)完备空间是否正交归一？ 设晶体中第m个原子的位矢为： Rn=m,+m,2+m,4.(5-4-1) 若将该原子看作一个孤立原子，则在其附近运动的电子将处于原子的某束缚态，(-R),该 波函数满足方程： -2+-Rg-R=880-R.（5-42） 其中V(r-R)为上述第m个原子的原子势场，6是与束缚态g相对应的原子能级。如果晶体 为N个相同的原子构成的布喇菲格子，则在各原子附近将有N个相同能量6，的束缚态波函数 ?。因此不考虑原子之间相互作用的条件下，晶体中的这些电子构成一个N个简并的系统： 能量为6，的N度简并态，(r-R),m=l,2,.,N。 实际晶体中的原子并不是真正孤立、完全不受其它原子影响的。由于晶体中其它诸原子 势场的微扰，系统的简并状态将消除，而形成由N个能级构成的能带。根据以上的分析和量 子力学的微扰理论，我们可以取上述N个简并态的线性组合 w(k,r）=∑an(k)g,r-R). .(5-4-3)

3 每个能带都包含 N 个 k 值。由于能带从原子的能级演化而来，所以内层电子能带常用原子 能级的量子数标记，如 3s,3p,3d 等。若原子所处原子势场的作用较之其它原子势场的作用要 大得多，例如对于原子中内层电子，或晶体间距较大时，上面讨论的近自由电子近似就不适 用，这时共有化运动状态与束缚态之间有直接联系，即紧束缚近似理论。 紧束缚理论的实质是把原子间相互作用影响看成微扰的简并微扰方法，微扰后的状态是 N 个简并态的线性组合，即用原子轨道 ( ) i m r R− 的线性组合来构成晶体中的电子共有化运动 的轨道  ( , ) k r ，也称原子轨道线性组合法，简写为 LCAO。 教师总结：通过讨论，使学生明白能带的形成只和原子间的结合有关，而和原子间的结合状 态无关，即：能带理论不仅适用于晶体，也适用于非晶体。 5.4.2 原子轨道线性组合 问题引入：在上述处理思想的基础上，如何用我们已有的知识点进行表征？ 提示点：1）近自由电子近似能否处理？ 2）如何构筑完备空间表征？ 3）完备空间是否正交归一？ 设晶体中第 m 个原子的位矢为： R a a a m = + + m m m 1 1 2 2 3 3 .（5-4-1） 若将该原子看作一个孤立原子，则在其附近运动的电子将处于原子的某束缚态 ( ) i m r R− ，该 波函数满足方程： 2 2 ( ) ( ) ( ) 2 V m i m i i m m      −  + − − = −     r R r R r R .（5-4-2） 其中 ( ) V − m r R 为上述第 m 个原子的原子势场， i  是与束缚态 i 相对应的原子能级。如果晶体 为 N 个相同的原子构成的布喇菲格子，则在各原子附近将有 N 个相同能量 i  的束缚态波函数 i 。因此不考虑原子之间相互作用的条件下，晶体中的这些电子构成一个 N 个简并的系统： 能量为 i  的 N 度简并态 ( ) i m r R− ，m=1，2，.，N。 实际晶体中的原子并不是真正孤立、完全不受其它原子影响的。由于晶体中其它诸原子 势场的微扰，系统的简并状态将消除，而形成由 N 个能级构成的能带。根据以上的分析和量 子力学的微扰理论，我们可以取上述 N 个简并态的线性组合 ( , ) ( ) ( ) m i m m   k r k r R = − a .（5-4-3）

作为晶体电子共有化运动的波函数，同时把原子间的相互影响当作周期势场的微扰项，于是 晶体中电子的薛定谔方程为： 2m 其中晶体势场U是由原子势场构成的，即 U(r）=∑(r-R)=U(r+R).(5-4-5) 5.4.3微扰计算（精讲） (5-44)式可以转化为如下形式： [-v+r(r-R)+U()-r(r-R)v(r)-EMr) 2m 代入(5-4-2)和(54-3)后，可得： ∑a.e-E)+U）-'v-Rlac-R.)=0. .(5-4-5) 紧束缚近似作用下，可认为原子间距较态的轨道大得多，不同原子的%重叠很小，从而有 [m(r-Rn,(r-Rn）d=6nm.(5-4-6) 现以g(r-R)左乘方程(5-45)，并对整个晶体积分，可以得： a(-E)+>agi(r-R)U(r)-V(r-R)(r-R)dr=0(5-4-7) 首先讨论(5-4-7)式中的积分。我们引入新的积分变量，令S=r-R,由品格周期性可知： U(5)=U(r-R)=U(r),则(5-4-7)式中积分可表示为： Jg[5-(R-R)][U(5)-r(5)]p,(5)d5=-J(R。-R).(5-4-8) 上式表明积分值仅取决于原子的相对位置R-R,因此引入符号J(R,-R)。式中引入负号 的理由是晶体势场与原子势场的差值U(5)-V(5)为负值。 将式(5-4-8)代入(5-47)式得到方程组： -∑a.(R-R)=(E-6)a. .(54-9) 不难证明：大“ 为满足方程组(549)的解，于是得到：E-6=-∑J(R-R)e

4 作为晶体电子共有化运动的波函数，同时把原子间的相互影响当作周期势场的微扰项，于是 晶体中电子的薛定谔方程为： 2 2 ( ) ( ) ( ) 2 U E m     −  + =     r r r .（5-4-4） 其中晶体势场 U(r)是由原子势场构成的，即 ( ) ( ) ( ) n l n U V U r r R r R = − = +  .（5-4-5） 5.4.3 微扰计算（精讲） （5-4-4）式可以转化为如下形式： ( ) ( ) 2 2 ( ) ( ) ( ) 2 V U V E m m m     −  + − + − − =     r R r r R r r 代入（5-4-2）和（5-4-3）后，可得： [( ) ( ) ( )] ( ) 0 m i m i m m a E U V   − + − − − = r r R r R .（5-4-5） 紧束缚近似作用下，可认为原子间距较 i 态的轨道大得多，不同原子的 i 重叠很小，从而有： ( ) ( ) * i n i m nm    − − = d  r R r R r .（5-4-6） 现以 ( ) * i n r R− 左乘方程（5-4-5），并对整个晶体积分，可以得： * ( ) ( )[ ( ) ( )] ( ) n i m i m m i m m a E a U V d 0    − + − − −  −   r R r r R r R r = .（5-4-7） 首先讨论（5-4-7）式中的积分。我们引入新的积分变量，令 = − m  r R ，由晶格周期性可知： U U U ( ) = − = (r R r m ) ( ) ，则（5-4-7）式中积分可表示为： ( ) ( ) ( ) ( ) * ( )   i n m i n m     − − = − − U V d           － R R J R R .（5-4-8） 上式表明积分值仅取决于原子的相对位置 R R n m − ，因此引入符号 ( ) J R R n m − 。式中引入负号 的理由是晶体势场与原子势场的差值 U V (  ) − ( ) 为负值。 将式（5-4-8）代入（5-4-7）式得到方程组： m n m i n ( ) ( ) m −  − = − a E a J R R  .（5-4-9） 不难证明： 1 i m m a e N = k R 为满足方程组（5-4-9）的解，于是得到： ( ) i ( m n ) i n m m E e   − − = − −   k R R J R R

亦即E=6-∑J(R-R)e=6-∑J(R)e.(5410) 式中R=R-R为原子的相对位置，与原子标号码m或n无关。(5-4l0)式实际上即为晶 体中共有化运动的电子的能量本征值。与该本征值相对应的电子共有化波函数为： 0=2-)（54 容易验证，上式所给出的波函数确为布洛赫函数。不妨作下面的变换， 0cΣ-ta-R)542四 进一步可得：0-太4（5413》 显然，4，(r)=4,(r+R)是和晶格周期相同的周期函数。 54.4一个简单的例子（提升应用所学理论处理实际问题的能力） 下面介绍一个紧束缚近似计算的简单例子一一简立方晶格中由原孤立原子s态口，形成的 能带，并分析其能带宽度。为应用上面的(5-4-10)式来计算能带函数，我们首先考查该式 中的积分项： ∫g'[5-R][U(5)-V(5)]g,(5)d5=-JR,).(5-414) 被积函数中②(G-R)和9，(G)表示相距为R,的两个原子的s态波函数，显然仅当它们有一定 重叠时，积分值才不为零。而当R=0时，波函数重叠最大，对此我们以 J。=-lm,(5)[U(5）)-V(5)]d5.(5-4-15) 表示。其次是R不为零时，对于简立方结构结构而言，则意味着有六个最近邻原子，即： (a,0,0),(0,a,0),(0,0,a),(-a,0,0),(0,-a,0),(0,0,-a)。 对于s态，波函数是球对称的，因而J(R)仅取决于原子间的距离R,而与R的方向无关。 则六个最近邻原子具有相同的(R)值，不妨用J,表示。对于相对距离大于最近邻R,的其它 积分项，由于重叠很小可以忽略不计。因此，(54-10)式可以写为： -6-人-A4.《6416 设k=k,i+k,广+kk,代入上面六个最近邻的R,可以得到：

5 亦即 ( ) ( ) ( ) i i m n s ( ) i n m i s m m E e e    −  − = − −  = −    k R R k R J R R J R .（5-4-10） 式中 R R R s n m = − 为原子的相对位置，与原子标号码 m 或 n 无关。（5-4-10）式实际上即为晶 体中共有化运动的电子的能量本征值。与该本征值相对应的电子共有化波函数为： 1 ( ) ( ) i m i m m e N    = −  k R k r r R .（5-4-11） 容易验证，上式所给出的波函数确为布洛赫函数。不妨作下面的变换， 1 ( ) ( ) ( ) i i m k i m m e e N    −  − = − −  k r k r R r r R .（5-4-12） 进一步可得： 1 ( ) ( ) i e u N   = k r k k r r .（5-4-13） 显然， ( ) ( )l u u k k r r R = + 是和晶格周期相同的周期函数。 5.4.4 一个简单的例子（提升应用所学理论处理实际问题的能力） 下面介绍一个紧束缚近似计算的简单例子——简立方晶格中由原孤立原子 s 态  s 形成的 能带，并分析其能带宽度。为应用上面的（5-4-10）式来计算能带函数，我们首先考查该式 中的积分项：   ( ) ( ) ( ) * ( )   i s i s   U V d − = −  －        R J R .（5-4-14） 被积函数中 * ( )   i s − R 和 ( )  i 表示相距为 R s 的两个原子的 s 态波函数，显然仅当它们有一定 重叠时，积分值才不为零。而当 0 R s = 时，波函数重叠最大，对此我们以 ( ) ( ) 2 0 ( ) i J U V d = − −           .（5-4-15） 表示。其次是 R s 不为零时，对于简立方结构结构而言，则意味着有六个最近邻原子，即： （a,0,0），（0,a,0），（0,0,a），（-a,0,0），（0,-a,0），（0,0,-a）。 对于 s 态，波函数是球对称的，因而 ( ) s J R 仅取决于原子间的距离 R s ，而与 R s 的方向无关。 则六个最近邻原子具有相同的 ( ) s J R 值，不妨用 1 J 表示。对于相对距离大于最近邻 R s 的其它 积分项，由于重叠很小可以忽略不计。因此，（5-4-10）式可以写为： ( ) 0 1 s s i E J J e i  −  = = − −  最近 k R R k .（5-4-16） 设 x y z k i j k = + + k k k ，代入上面六个最近邻的 R s ，可以得到：