
11/1/2024 §5-1 齿轮机构的应用和分类 (5)渐开线的形状取决于 基圆的大小 。 基圆愈小,渐开线愈弯曲;基圆 愈大,渐开线愈平直。当基圆半 径为无穷大,其渐开线将成为一 条直线。 (6)渐开线上各点压力角 不等,离基圆越远压力角越 大
11/1/2024 §5-1 齿轮机构的应用和分类 (5)渐开线的形状取决于 基圆的大小 。 基圆愈小,渐开线愈弯曲;基圆 愈大,渐开线愈平直。当基圆半 径为无穷大,其渐开线将成为一 条直线。 (6)渐开线上各点压力角 不等,离基圆越远压力角越 大

11/1/2024 §5-1 齿轮机构的应用和分类 齿廓在K点所受正压力的方向线为KB, 齿轮绕O点转动时,K点速度方向线为Kv, 两者之间所夹的锐角称为渐开线在K点 的压力角,用 表示, 由△OBK可知: 向径:
11/1/2024 §5-1 齿轮机构的应用和分类 齿廓在K点所受正压力的方向线为KB, 齿轮绕O点转动时,K点速度方向线为Kv, 两者之间所夹的锐角称为渐开线在K点 的压力角,用 表示, 由△OBK可知: 向径:

11/1/2024 §5-1 齿轮机构的应用和分类 3、渐开线方程式 以O为极点,OA为极轴,建立渐开线 的极坐标方程。 由△OBK可知: 向径: 极角: 称为压力角 的渐开线函数, 工程上用 表示 渐开线的极坐标方程式:
11/1/2024 §5-1 齿轮机构的应用和分类 3、渐开线方程式 以O为极点,OA为极轴,建立渐开线 的极坐标方程。 由△OBK可知: 向径: 极角: 称为压力角 的渐开线函数, 工程上用 表示 渐开线的极坐标方程式:

11/1/2024 §5-1 齿轮机构的应用和分类 二、渐开线齿廓 1、啮合线为一条定直线 如图所示,一对渐开线齿廓在点 K 啮合,过K作公法线必切于 基圆,成为两基圆的一条内公 切线。这条内公切线就是啮合 点K 走过的轨迹,称为啮合线。 在两基圆的大小和位置都确定的 情况下,在同一方向上只有一 为一条定直线。 2、能实现定传动比传动要 由于啮合线为一条定直线,故 求 C点为一定点,所以能实现定 传动比传动。传动比为: 条内公切线,所以,啮合线
11/1/2024 §5-1 齿轮机构的应用和分类 二、渐开线齿廓 1、啮合线为一条定直线 如图所示,一对渐开线齿廓在点 K 啮合,过K作公法线必切于 基圆,成为两基圆的一条内公 切线。这条内公切线就是啮合 点K 走过的轨迹,称为啮合线。 在两基圆的大小和位置都确定的 情况下,在同一方向上只有一 为一条定直线。 2、能实现定传动比传动要 由于啮合线为一条定直线,故 求 C点为一定点,所以能实现定 传动比传动。传动比为: 条内公切线,所以,啮合线
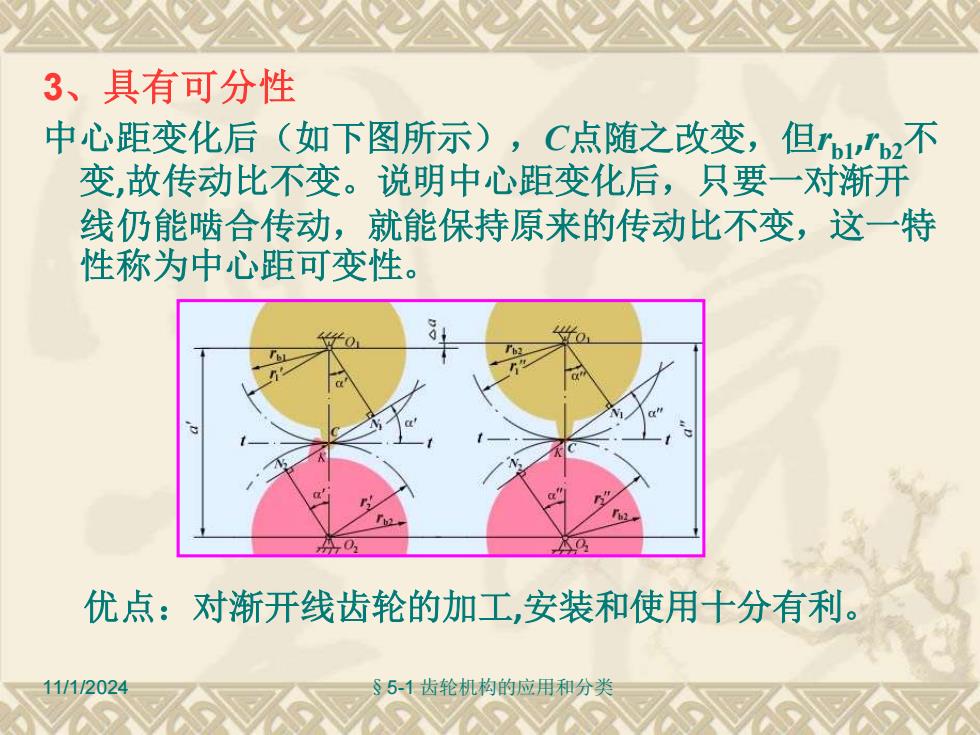
11/1/2024 §5-1 齿轮机构的应用和分类 3、具有可分性 中心距变化后(如下图所示),C点随之改变,但rb1,rb2不 变,故传动比不变。说明中心距变化后,只要一对渐开 线仍能啮合传动,就能保持原来的传动比不变,这一特 性称为中心距可变性。 优点:对渐开线齿轮的加工,安装和使用十分有利
11/1/2024 §5-1 齿轮机构的应用和分类 3、具有可分性 中心距变化后(如下图所示),C点随之改变,但rb1,rb2不 变,故传动比不变。说明中心距变化后,只要一对渐开 线仍能啮合传动,就能保持原来的传动比不变,这一特 性称为中心距可变性。 优点:对渐开线齿轮的加工,安装和使用十分有利