
2.1波动方程与平面波 4 电子科技大学计算电磁学及其应用团队,CEMLAB ab /958 2.1.2平面波的叠加-行波与驻波 考虑两组平面波:①E支=Aekz,H时=Aez ②E=Bek,H=-ea 其叠加场为 Ex Ae-jkz Bejkz Hy =(Ae-jkz-Bejkz) 当A=0或B=0时,Ex和H,纯行波: 当A=B时,Ex=2Ac0skz,驻波: 当A=-B时,Ex=-2 jA sin kz,驻波; 当|A|≠|B吲时Ex=V2+B2+2 AB cosk2 e-jtan-1顶8 tan kz] 12
12 电子科技大学计算电磁学及其应用团队,CEMLAB 12 其叠加场为 2.1.2 平面波的叠加 -行波与驻波 2.1 波动方程与平面波

2.1波动方程与平面波 13 电子科技大学计算电磁学及其应用团队,CEMLAB 1956 IAl+IBI 驻波图 IAL-BI λM2 Z 定义驻波比SWR= IAI+BI IAI-1BI SWR的取值范围1<SWR<+o 假设①为入射波,②为反射波,则反射系数「=月 驻波比SWR= Al+rIAl -1+Irl lAl-TIAI1- (S11=20logr,回波损耗RL=-S11) 天线驻波比:(1)超宽带VSWR<2,(2)窄带VSWR<1.5 13
13 电子科技大学计算电磁学及其应用团队,CEMLAB 13 定义驻波比 𝐒𝐖𝐑 ൌ 𝜜 ା 𝜝 𝜜 ି 𝜝 SWR的取值范围1 ൏ 𝐒𝐖𝐑 ൏ ∞ 假设①为入射波,②为反射波,则反射系数𝜞 ൌ 𝜝 𝜜 驻波比𝐒𝐖𝐑 ൌ ௮ ା௰ ௮ ି௰ = ଵା ௰ ଵି ௰ ,( 𝑆ଵଵ ൌ 20 𝑙𝑜𝑔 𝛤 ,回波损耗RL=െ𝑆ଵଵ ) 天线驻波比:⑴超宽带VSWR<2, ⑵窄带VSWR<1.5 2.1 波动方程与平面波 驻波图

2.1波动方程与平面波 电子科技大学计算电磁学及其应用团队,CEMLAB ab 1956 对行波和驻波的理解(从时域角度) 入射波 (z向行波) 合成波 (驻波) 反射波 (-z向行波) 电场强度 磁场强度
14 电子科技大学计算电磁学及其应用团队,CEMLAB 2.1 波动方程与平面波 对行波和驻波的理解(从时域角度) (z向行波 ) (驻波 ) 电场强度 磁场强度 入射波 合成波 反射波 (-z向行波 )
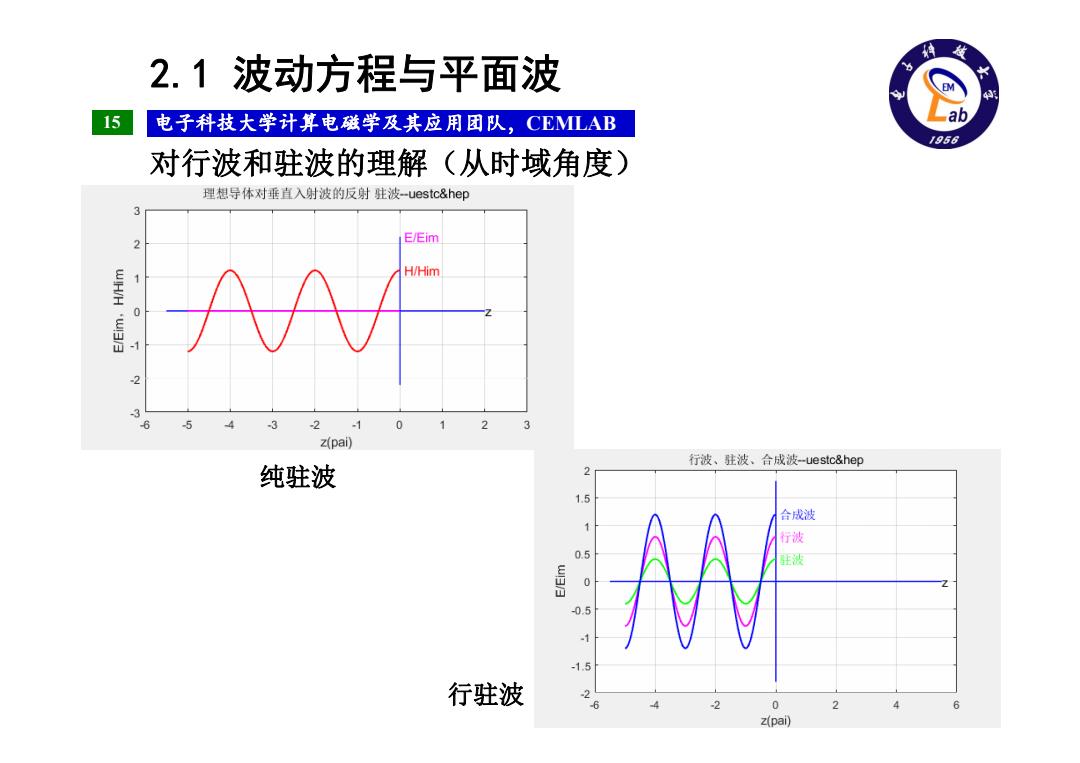
2.1波动方程与平面波 4 15 电子科技大学计算电磁学及其应用团队,CEMLAB 1956 对行波和驻波的理解(从时域角度) 理想导体对垂直入射波的反射驻波-uestc&hep 2 E/Eim H/Him WH/H 'w 0 -1 -2 6 -5 3 -21 0 2 z(pai) 行波、驻波、合成波-ue stc&hep 纯驻波 2 合成波 行波 0.5 0.5 15 行驻波 -6 2 0 z(pai)
15 电子科技大学计算电磁学及其应用团队,CEMLAB 2.1 波动方程与平面波 对行波和驻波的理解(从时域角度) 纯驻波 行驻波

2.1波动方程与平面波 16 电子科技大学计算电磁学及其应用团队,CEMLAB 1956 练习:对于A=B的纯驻波,试证明此时无能量传播 (s=Re(S)=0) Ex Ae-jkz Bejkz E.=2Acos亿,H,=-24sine 7 1 Hy=(Ae-jkz-Bejkz) S=Ex开=立2M sin 2kz 或时域 8,=2v2Acos k=cos@t 光,=22 sin k-sinor 7 5=ex孔=i24 sin 2kz sin 2@t &=7&h=0 16 故无能量传播
16 电子科技大学计算电磁学及其应用团队,CEMLAB 16 练习:对于A=B的纯驻波,试证明此时无能量传播 ( Re 0) S 2 cos Ex A kz , 2 sin y jA H kz 2 * 2 ˆ sin 2 z jA S E H u kz 或时域 2 0 2 2 cos cos 2 2 sin sin 2 ˆ sin 2 sin 2 1 0 x y z T A kz t A kz t A u kz t dt T 故无能量传播。 2.1 波动方程与平面波