1.1矢量分析 6 电子科技大学计算电磁学及其应用团队,CEMLAB ab /858 1.1.2梯度、散度、旋度 Vφ 梯度表示变化率最大值及 变化最快的方向 Surface: =fx,) V.4=lim fads 散度表示物理量A在某点处(△v→0) △v→0 △v 流出闭合球面S的多少(通量) 数学运算 V.A=9 6A. x ay 6
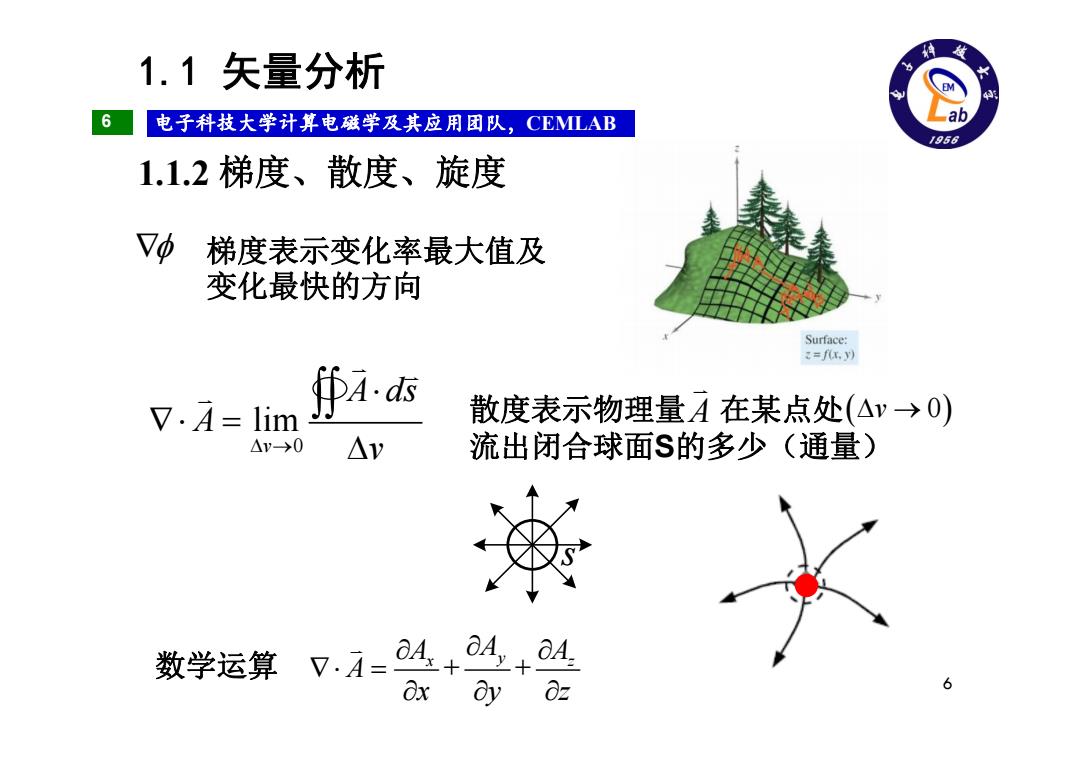
6 电子科技大学计算电磁学及其应用团队Computational Electromagnetics Laboratory, UESTC ,CEMLAB 6 1.1 矢量分析 1.1.2 梯度、散度、旋度 梯度表示变化率最大值及 变化最快的方向 0 limv A ds A v 散度表示物理量 在某点处 流出闭合球面 S的多少(通量) A v 0 s 数学运算 + + x y z A A A A x y z

1.1矢量分析 电子科技大学计算电磁学及其应用团队,CEMLAB ⊙6 与散度表示流动通量不同,叉乘表示旋转(矢量方向的改变) i×i,=i 因此,数学上旋度又×A表示既有矢量大小随空间位置 的变化(通过偏微分算法又体现),又有矢量方向的变 化(即旋转,通过叉乘×体现)。 物理上,旋度表示涡旋源
7 电子科技大学计算电磁学及其应用团队Computational Electromagnetics Laboratory, UESTC ,CEMLAB 7 1.1 矢量分析 与散度表示流动通量不同,叉乘表示旋转(矢量方向的改变) ˆ ˆ ˆ x y z uu u 因此,数学上旋度 表示既有矢量大小随空间位置 的变化(通过偏微分算法 体现),又有矢量方向的变 化(即旋转,通过叉乘 体现)。 A 物理上,旋度表示涡旋源

1.1矢量分析 8 电子科技大学计算电磁学及其应用团队,CEMLAB Lab 1058 1.1.3常用矢量运算关系式 V×(V)=0 7(×A)=0 7.Ad=承A 散度定理 V×A=∮Adl Stokes定理 直角坐标、圆柱坐标、球坐标的转换及梯度、散度、 旋度形式见教材附录A。 8
8 电子科技大学计算电磁学及其应用团队Computational Electromagnetics Laboratory, UESTC ,CEMLAB 8 1.1 矢量分析 1.1.3 常用矢量运算关系式 =0 A 0 v S Adv A ds 散度定理 S C A ds A dl Stokes定理

第1章基本电磁理论-目录 9 电子科技大学计算电磁学及其应用团队,CEMLAB Lab 958 1.1矢量分析 1.2正弦电磁场及其表示 1.3 Maxwell方程、本构关系、边界条件 1.4 Helmholtz方程 1.5电磁场方程基本求解方法 9
9 电子科技大学计算电磁学及其应用团队Computational Electromagnetics Laboratory, UESTC ,CEMLAB 9 第1章 基本电磁理论-目录 1.1 矢量分析 1.2 正弦电磁场及其表示 1.3 Maxwell方程、本构关系、边界条件 1.4 Helmholtz方程 1.5 电磁场方程基本求解方法

1.2正弦电磁场及其表示 10 电子科技大学计算电磁学及其应用团队,CEMLAB ab J858 1.2.1正弦场(时谐场) 正弦电磁场又称时谐电磁场,是指随时间按正弦(或余 弦)函数变化的电磁场,或者按指数ejor(或ejor)变化 的电磁场(取其实部)。 E(元,t)=Re(E(r)eo) 花体:瞬时量 正体:复数量(教材1-7节) 上述定义中的幅值 E(F)为幅度峰值(peak value),若定义为 有效值(均方根值),则需乘上√的系数,即教材中的定义0
10 电子科技大学计算电磁学及其应用团队Computational Electromagnetics Laboratory, UESTC ,CEMLAB 10 1.2 正弦电磁场及其表示 1.2.1 正弦场(时谐场) 正弦电磁场又称时谐电磁场,是指随时间按正弦(或余 弦)函数变化的电磁场,或者按指数 (或 )变化 的电磁场(取其实部)。 j t e - j t e Re( ( ) ) j ωt r, t = E r e ( ) 花体:瞬时量 正体:复数量(教材1-7节) 上述定义中的幅值 为幅度峰值(peak value ), 若定义为 有效值(均方根值),则需乘上 的系数,即教材中的定义 E r( ) 2