
二、逐点比校法插补 (4)终点判断(三种方法) a)设置一个减法计数器,在其中存入∑=x.+y.,X或Y 坐标方向进给时均在计数器中减去1,当∑=0时,停止插补。 b)设置∑x和∑y两个减法计数器,在其中分别存入终点坐标值 X。和y。,X或Y坐标方向每进给一步时,就在相应的计数器 中减去1,直到两个计数器都为0时,停止插补。 C)选终点坐标值较大的坐标作为计数坐标,用其终值作为计数器初值, 仅在该轴走步时才减去1,当减到0时,停止插补。 主页 目录 上一页 下一页 后退 退出
二、逐点比较法插补 中减去1, (4)终点判断(三种方法) a) 设置一个减法计数器,在其中存入 ,X或Y 坐标方向进给时均在计数器中减去1,当 时,停止插补。 b) 设置 和 两个减法计数器,在其中分别存入终点坐标值 ,X或Y坐标方向每进给一步时,就在相应的计数器 直到两个计数器都为0时,停止插补。 C)选终点坐标值较大的坐标作为计数坐标,用其终值作为计数器初值, 仅在该轴走步时才减去1,当减到0时,停止插补。 和 x y = + e e x y = 0 e y e x
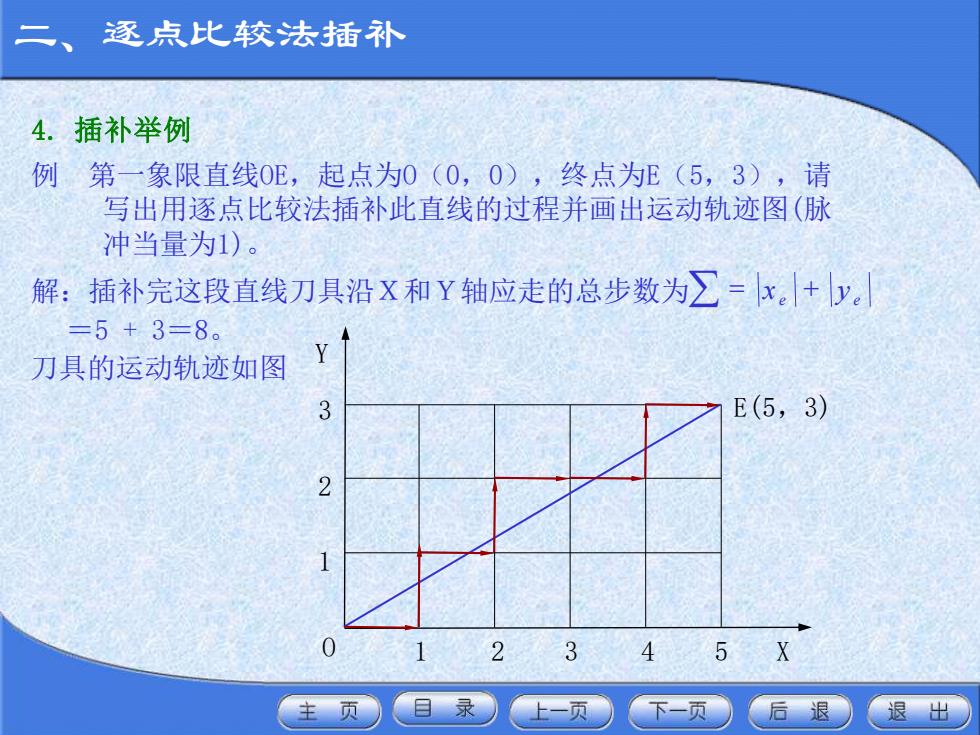
二、 逐点比较法插补 4.插补举例 例第一象限直线0E,起点为0(0,0),终点为E(5,3),请 写出用逐点比较法插补此直线的过程并画出运动轨迹图(脉 冲当量为1)。 解:插补完这段直线刀具沿X和Y轴应走的总步数为∑=x。+y。 =5+3=8。 刀具的运动轨迹如图 3 E(5,3) 5 主页●目录 上一页 下一页 后退 退出
二、逐点比较法插补 Y O 1 2 3 1 2 3 4 5 X E(5,3) 例 第一象限直线OE,起点为O(0,0),终点为E(5,3),请 写出用逐点比较法插补此直线的过程并画出运动轨迹图(脉 冲当量为1)。 解:插补完这段直线刀具沿X和Y轴应走的总步数为 =5 + 3=8。 刀具的运动轨迹如图 = + e e x y 4. 插补举例
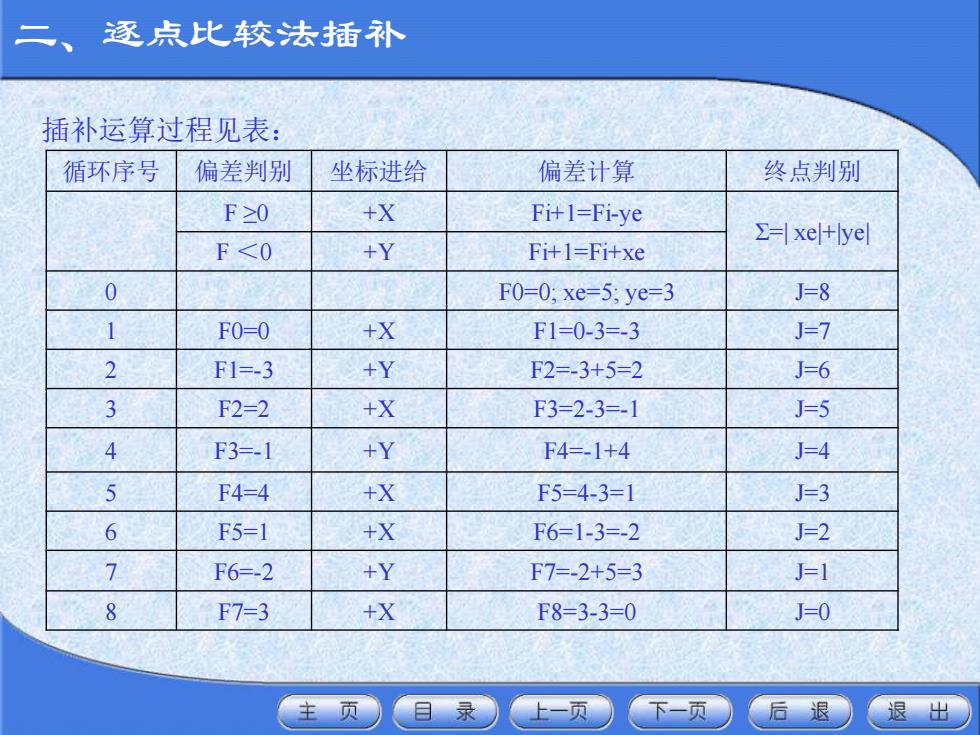
二、 逐点比较法插补 插补运算过程见表: 循环序号 偏差判别 坐标进给 偏差计算 终点判别 F≥0 +X Fi+l=Fi-ye =xel+lyel F<0 +Y Fi+1=Fi+xe F0=0;xe=5;ye=3 J=8 1 F0=0 +X F1=0-3=-3 =7 2 F1=-3 +Y F2=-3+5=2 J=6 3 F2=2 +X F3=2-3=-1 J=5 4 F3=-1 +Y F4=-1+4 J=4 5 F4=4 +X F5=4-3=1 J=3 6 F5=1 +X F6=1-3=-2 J=2 7 F6=-2 +Y F7=-2+5=3 J=1 8 F7=3 +X F8=3-3=0 J=0 主页 目录 一页 一页 后退 退出
二、逐点比较法插补 循环序号 偏差判别 坐标进给 偏差计算 终点判别 F ≥0 +X Fi+1=Fi-ye Σ=| xe|+|ye| F <0 +Y Fi+1=Fi+xe 0 F0=0; xe=5; ye=3 J=8 1 F0=0 +X F1=0-3=-3 J=7 2 F1=-3 +Y F2=-3+5=2 J=6 3 F2=2 +X F3=2-3=-1 J=5 4 F3=-1 +Y F4=-1+4 J=4 5 F4=4 +X F5=4-3=1 J=3 6 F5=1 +X F6=1-3=-2 J=2 7 F6=-2 +Y F7=-2+5=3 J=1 8 F7=3 +X F8=3-3=0 J=0 插补运算过程见表:

二、 逐点比较法插补 5.圆弧插补 (1)偏差计算公式 以第一象限逆圆弧为例,起点为S,终点为E,半径为r,圆心在原点。 再设刀具刀位点某一时刻位于点,它在圆弧上,有:x+=r2: 若位于A(a,ya)点,它在圆弧的外部,有:x好+y2>r2, 若位于C(。,y)点,它在圆弧的内部,有:x2+y2<r 令F=x2+y2-r2为偏差判别函数,由即可判别刀位点与圆孤的位置 关系,判别方法如下: F>0,刀位点在圆弧外部 F =0,刀位点在圆弧上 F<0,刀位点在圆弧内部 主页。 目录 上一页 下一页 后退 退出
二、逐点比较法插补 5.圆弧插补 (1)偏差计算公式 以第一象限逆圆弧为例,起点为S,终点为E,半径为r,圆心在原点。 再设刀具刀位点某一时刻位于点,它在圆弧上,有: ; 若位于 点,它在圆弧的外部,有: , 若位于 点,它在圆弧的内部,有: 。 令 为偏差判别函数,由即可判别刀位点与圆弧的位置 关系,判别方法如下: 2 2 2 x y r b b + = 2 2 2 A(xa , ya ) xa + y a > r 2 2 2 ( ) xc + yc < r C xc yc , 2 2 2 F = x + y - r < = > ,刀位点在圆弧内部 ,刀位点在圆弧上 ,刀位点在圆弧外部 0 0 0 F F F

二、 逐点比较法插补 (2)进给 由F,的符号判别进给方向: F≥0,沿x方向走一步: (3)偏差计算公式简化 F<0,沿+y方向走一步。 设某时第一象限中某点为:D(x,y),其F值为:F=x2+y2-r2 x+1=x,+1 a)若F,≥0,沿+x方向走一步,则: y+1=y F1=yx。-x+y。=yx。-(X+1y=yx。-xy-y=Fy b)若F,<0,沿+y方向走一步,则: (y1+1=y,+1 FH=xH2+22=x2+0y+022=x2+2+2y+1=E+2y+1 (4)终点判断 与逐点比较法直线插补相同。 主页 目录 一页 一页 后退 退出
二、逐点比较法插补 (2)进给 由 的符号判别进给方向: (3)偏差计算公式简化 设某时第一象限中某点为: ,其F值为: a) 若 ≥0,沿+x方向走一步,则: b) 若 <0,沿+y方向走一步,则: (4)终点判断 与逐点比较法直线插补相同。 F i < + - ,沿 方向走一步。 ,沿 方向走一步; F y F x i i 0 0 ( , ) D xi yi = = + + + i i i i y y x x 1 1 1 F i Fi yi xe xi ye yixe xi ye yixe xi ye ye Fi ye + = + - + = -( +1) = - - = - 1 1 1 = + = + + 1 1 1 i i i i y y x x F i ( 1) 2 1 2 1 2 2 2 2 2 2 2 2 1 2 Fi+1 =xi+1 +yi+ r =xi + yi + r =xi +yi + yi + r =Fi + yi + 2 2 2 F = x + y - r