
§11一1质点和质点系的动量矩 一、 质点的动量矩 4、点的运动轨迹为平面曲线如何计算?联想? 1)类比为力矩直接计算 例题1 2)动量臂不便于计算?联想? P312-11 例题2 习题11-1P300 要用绝对速度计算动量矩(动量、动能)与力矩计算 一般不规定逆时针转动的动量矩为正 的不同之处 16
16 §11-1质点和质点系的动量矩 一、质点的动量矩 4、点的运动轨迹为平面曲线如何计算? 1)类比为力矩直接计算 例题1 2)动量臂不便于计算? 例题2 联想? 习题11-1 P300 要用绝对速度计算动量矩(动量、动能) 一般不规定逆时针转动的动量矩为正 与力矩计算 的不同之处 联想? P31 2-11

§11一1质点和质点系的动量矩 二、质点系动量矩 (理解定义) 1、对点的动量矩: Mm) 2、对轴的动量矩(即上式在各轴上的投影)? L.w,m 三、刚体的动量矩(重点掌握) 1、平移刚体 质心运动方程 平移刚体的运动特点:对点的: 对轴的: 结论:同于一个点的动量矩的计算P277 7
17 二、质点系动量矩(理解定义) 1、对点的动量矩: LO 2、对轴的动量矩(即上式在各轴上的投影)? Lz 三、刚体的动量矩(重点掌握) 1、平移刚体 质心运动方程 平移刚体的运动特点: 对点的: 对轴的: 结论:同于一个点的动量矩的计算P277 §11-1 质点和质点系的动量矩 ( ) 1 O i i n i M m v = = ( ) 1 z i i n i M m v = =
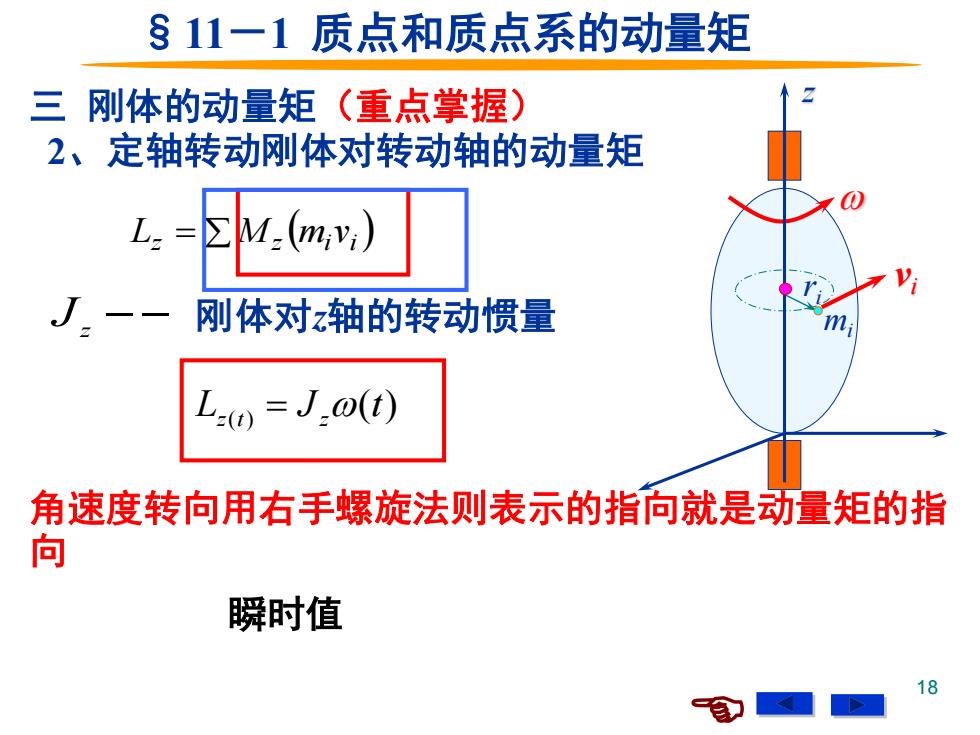
§11一1质点和质点系的动量矩 三 刚体的动量矩(重点掌握) 2、定轴转动刚体对转动轴的动量矩 L= 刚体对z轴的转动惯量 L0=J0(t) 角速度转向用右手螺旋法则表示的指向就是动量矩的指 向 瞬时值 18
18 2、定轴转动刚体对转动轴的动量矩 = ( ) z z i i L M m v J z − − 刚体对z轴的转动惯量 r vi i mi z 角速度转向用右手螺旋法则表示的指向就是动量矩的指 向 三 刚体的动量矩(重点掌握) ( ) ( ) L J t z t = z §11-1 质点和质点系的动量矩 瞬时值
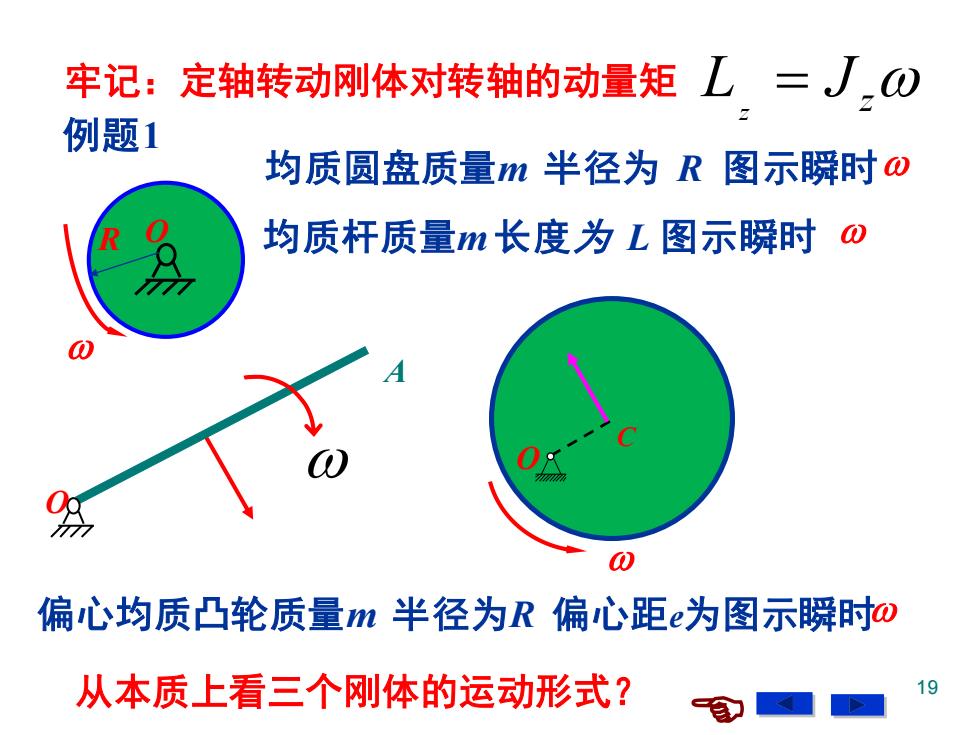
牢记:定轴转动刚体对转轴的动量矩L=J0 例题1 均质圆盘质量m半径为R图示瞬时ω 均质杆质量m长度为L图示瞬时⊙ 0 偏心均质凸轮质量m半径为R偏心距e为图示瞬时o 从本质上看三个刚体的运动形式? 9
19 均质圆盘质量m 半径为 R 图示瞬时 R O C 均质杆质量m 长度为 L 图示瞬时 偏心均质凸轮质量m 半径为R 偏心距e为图示瞬时 从本质上看三个刚体的运动形式? 牢记:定轴转动刚体对转轴的动量矩 L J z z = O A 例题1 O
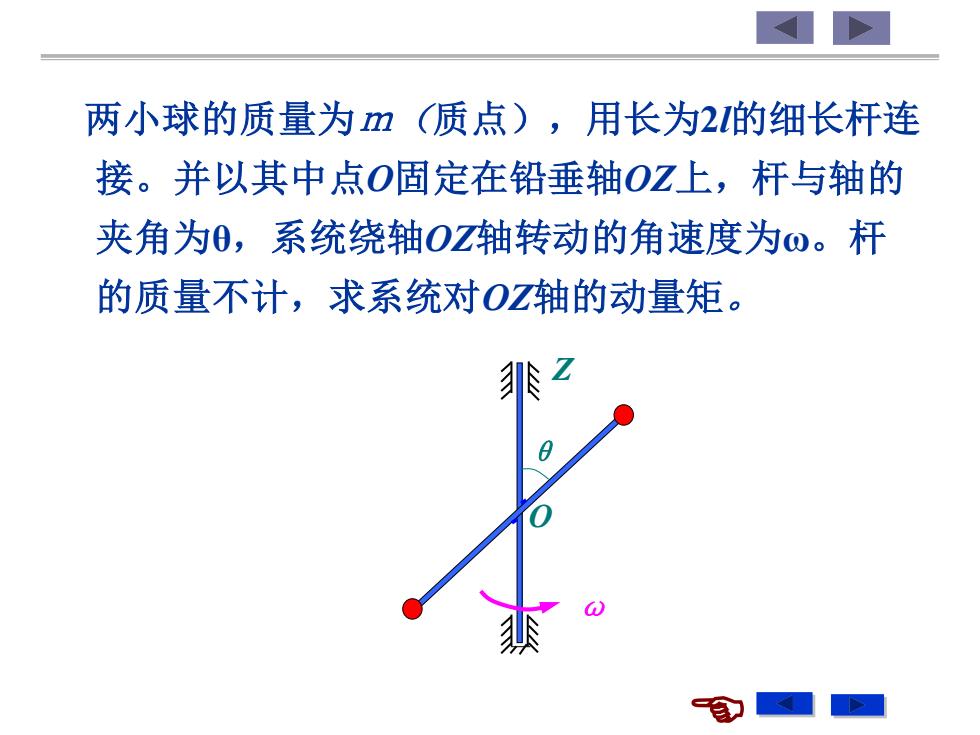
两小球的质量为m(质点),用长为2的细长杆连 接。并以其中点0固定在铅垂轴OZ上,杆与轴的 夹角为0,系统绕轴OZ轴转动的角速度为o。杆 的质量不计,求系统对OZ轴的动量矩
两小球的质量为m(质点),用长为2l的细长杆连 接。并以其中点O固定在铅垂轴OZ上,杆与轴的 夹角为θ,系统绕轴OZ轴转动的角速度为ω。杆 的质量不计,求系统对OZ轴的动量矩。 O Z ω θ