
THODE 寻求知识的途径 on &c chercher ciences. LA DIOPTRIOVE 仅接纳自己理解并可以排除疑问的东西 LAGEOM卫 RIE. ui foni des efais de cet METHODE 把大的因难拆分成小的困难 从简单到复杂的推理 De PImprimcric de【 MAIRE 进行检验
11 • 寻求知识的途径 仅接纳自己理解并可以排除疑问的东西 把大的困难拆分成小的困难 从简单到复杂的推理 进行检验

本章重点 大★女1计算平面图形上任一点的速度三种 方法(平面图形的角速度)两种方法★★ ★★大2计算平面图形上任一点的加速度 ·(平面图形角加速度)★★★ 12
12 本章重点 ❖ ★ ★ ★ 1 计算平面图形上任一点的速度三种 方法(平面图形的角速度) 两种方法★ ★ ❖★ ★ ★ 2 计算平面图形上任一点的加速度 ❖(平面图形角加速度) ★★★
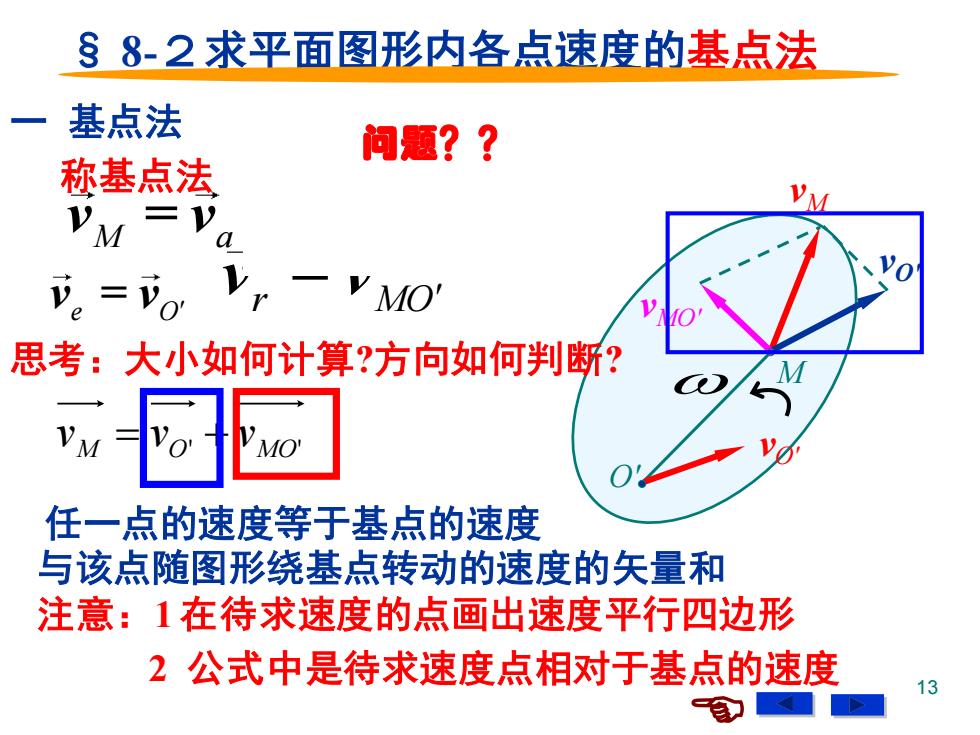
§8-2求平面图形内各点速度的基点法 一 基点法 问题?? 称基点法 VM 。=0 Y MO 思考:大小如何计算?方向如何判断? 任一点的速度等于基点的速度 与该点随图形绕基点转动的速度的矢量和 注意:1在待求速度的点画出速度平行四边形 2公式中是待求速度点相对于基点的速度 13 )
13 § 8-2求平面图形内各点速度的基点法 任一点的速度等于基点的速度 vM vO' vMO' O' vO' M v = v v v M a e r = + e O v = v 一 基点法 w r MO v = v 思考:大小如何计算?方向如何判断? 与该点随图形绕基点转动的速度的矢量和 称基点法 M O' MO' v = v + v 注意:1 在待求速度的点画出速度平行四边形 2 公式中是待求速度点相对于基点的速度 问题??
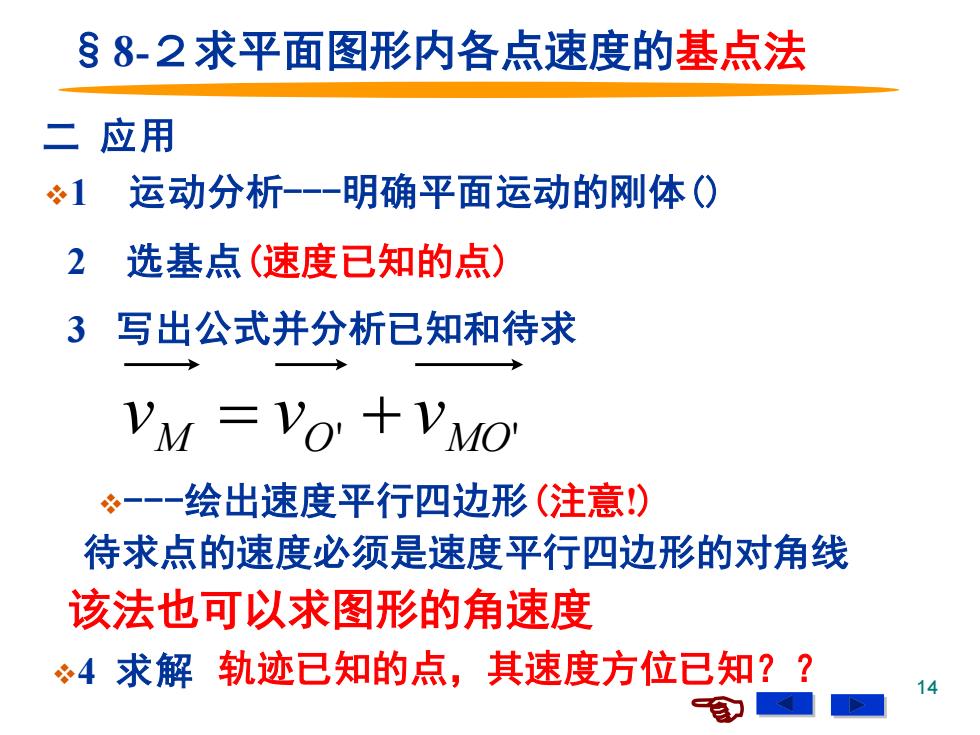
§8-2求平面图形内各点速度的基点法 二应用 必1 运动分析-明确平面运动的刚体() 2 选基点(速度已知的点) 3 写出公式并分析已知和待求 VM =Vo'+VMO 。一-一绘出速度平行四边形(注意!) 待求点的速度必须是速度平行四边形的对角线 该法也可以求图形的角速度 4求解轨迹已知的点,其速度方位已知??
14 二 应用 §8-2求平面图形内各点速度的基点法 ❖1 运动分析-明确平面运动的刚体() 2 选基点(速度已知的点) 3 写出公式并分析已知和待求 ❖-绘出速度平行四边形(注意!) ❖4 求解 该法也可以求图形的角速度 M O' MO' v = v + v 待求点的速度必须是速度平行四边形的对角线 轨迹已知的点,其速度方位已知??
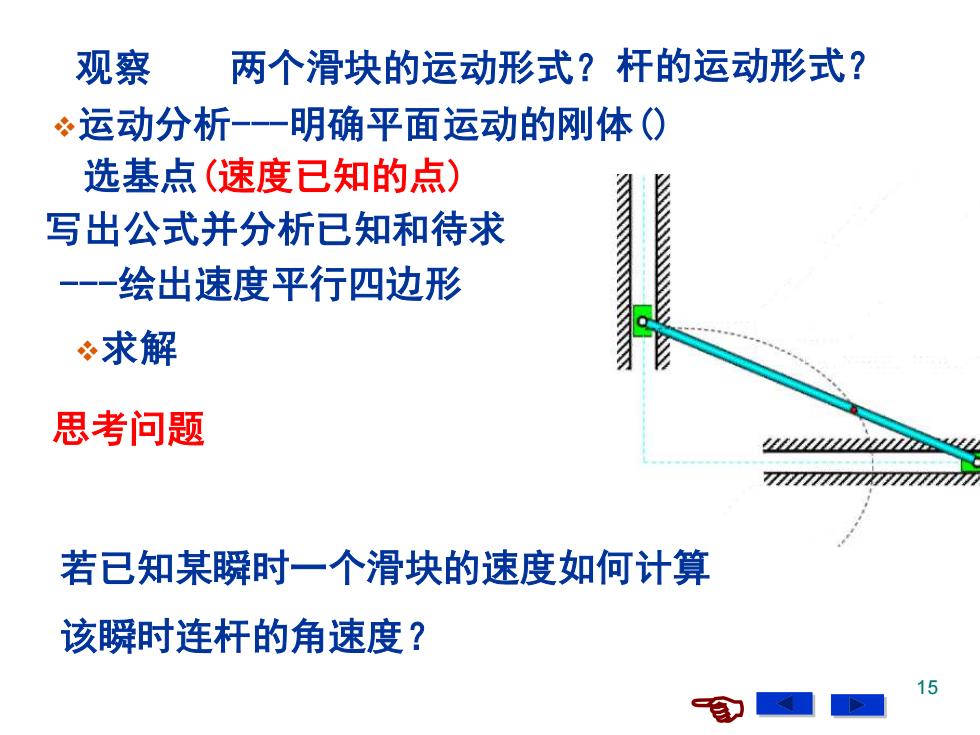
观察 两个滑块的运动形式?杆的运动形式? ÷运动分析-一明确平面运动的刚体0 选基点(速度已知的点) 写出公式并分析已知和待求 一一绘出速度平行四边形 求解 思考问题 若已知某瞬时一个滑块的速度如何计算 该瞬时连杆的角速度? 15
15 观察 两个滑块的运动形式?杆的运动形式? 思考问题 若已知某瞬时一个滑块的速度如何计算 该瞬时连杆的角速度? 选基点(速度已知的点) ❖运动分析-明确平面运动的刚体() 写出公式并分析已知和待求 -绘出速度平行四边形 ❖求解