
一海大理学院表号髁件 大学物理学电子教案 电磁感应— 磁场的能量 电磁场基本方程
大学物理学电子教案 海大理学院教学课件 电磁感应——磁场的能量 电磁场基本方程

复习 ·感生电动势 f.=-儿西 ·自感 Φ=LI 8,=-L dt ·互感 Φ21=MM1④12=M 821= dΦ21=-M dt dt dΦ2 =-M dt dt
复 习 • 感生电动势 dS t B E dl L S k = − • 互感 dt dI i = −L • 自感 F=LI F21 = MI 1 F12 = MI 2 dt dI M dt d 21 1 21 = − F =- dt dI M dt d 12 2 12 = − F =-
13-5磁场的能量 引入: 电容器充电,储存电场能量 w.-1qv-1cu 电场能量密度 w20000000 1 。=。E2 电流激发磁场,也要供给能量,所以磁场具有能量。 当线圈中通有电流时,在其周围建立了磁场,所储存的磁能 等于建立磁场过程中,电源反抗自感电动势所做的功
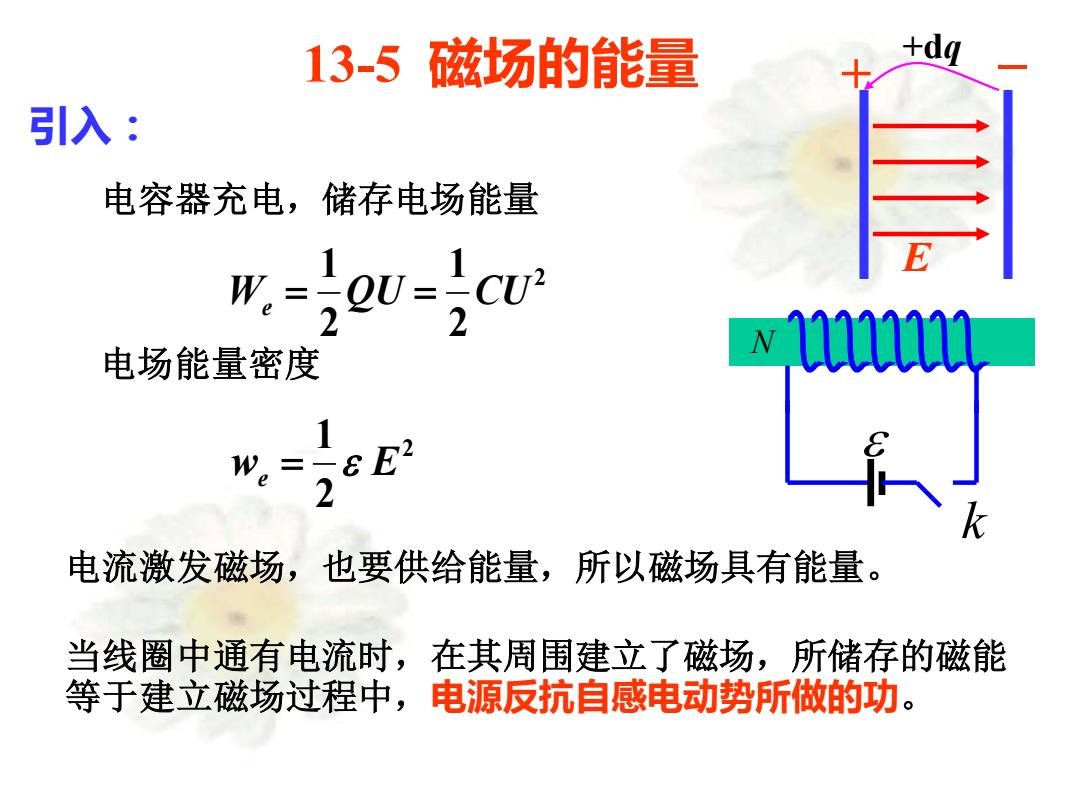
13-5 磁场的能量 引入: 电容器充电,储存电场能量 2 2 1 2 1 We = QU = CU 电流激发磁场,也要供给能量,所以磁场具有能量。 当线圈中通有电流时,在其周围建立了磁场,所储存的磁能 等于建立磁场过程中,电源反抗自感电动势所做的功。 N k 电场能量密度 2 2 1 we = E E +dq + _
线圈贮存的能量 自感磁能: 对于如图所示的电路 ε-L =RI d dt aldt LIdI RI'dt ∫sdt=∫LIdl+∫Rr2M 焦耳热 电源供给 磁场 的能量 的能量 自感线圈贮存的磁场 W.= LIdl=-LI 0
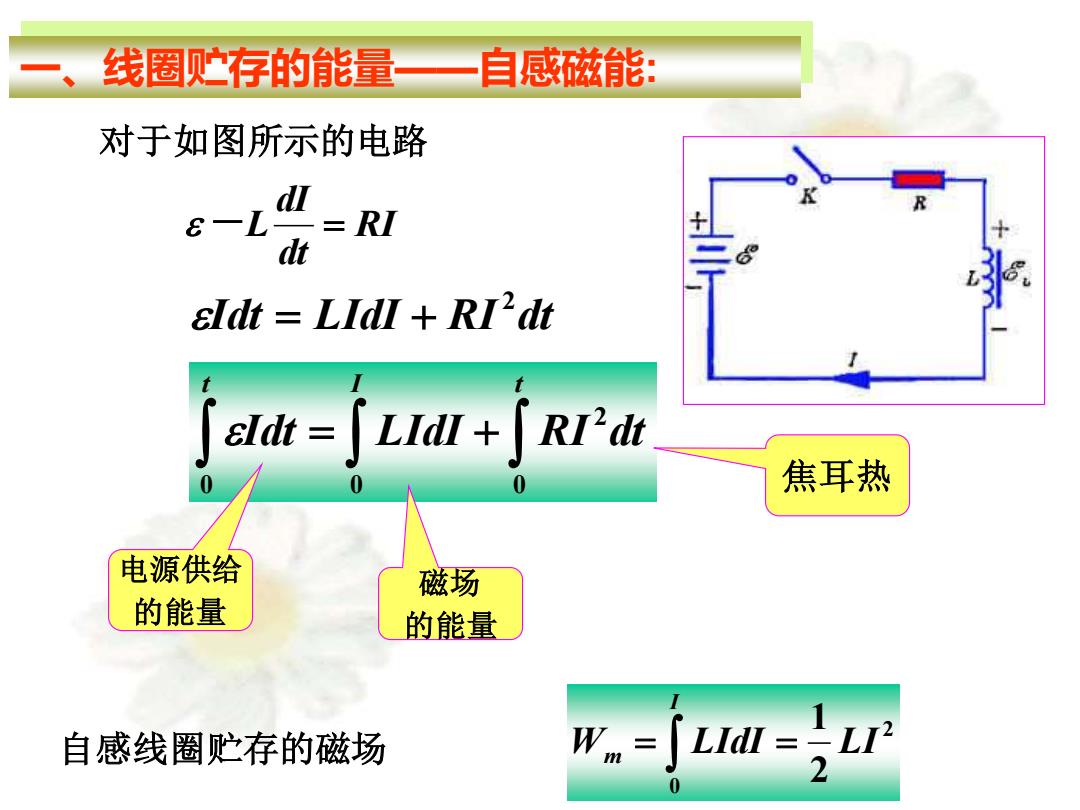
一、线圈贮存的能量——自感磁能: 对于如图所示的电路 RI dt dI -L = Idt LIdI RI dt 2 = + = + t I t Idt LIdI RI dt 0 2 0 0 电源供给 的能量 磁场 的能量 焦耳热 自感线圈贮存的磁场 2 0 2 1 W LIdI LI I m = =

二、 磁场的能量 以长直螺线管为例:当流有电流时 B=unl I=- B un L=un'y 长直螺线管的磁场能量:, 对于一般情况: 定义磁场的能量密度: B2 =-8. Wm Wm 2 24 磁场所储存的总能量: 磁场所储存的总能量: Wm = 2 dy 积分遍及磁场存在的全空间
二、磁场的能量 以长直螺线管为例:当流有电流I时 长直螺线管的磁场能量: 定义磁场的能量密度: 2 2 B wm = 磁场所储存的总能量: = = dV B Wm wm dV 2 2 B = nI n B I = L n V 2 = V B n B Wm LI n V 2 2 1 2 1 2 2 2 2 = = = 磁场所储存的总能量: = V m dV H B W 2 对于一般情况: 积分遍及磁场存在的全空间。 wm B H = 2 1