广东海洋大学：《大学物理》课程教学资源（PPT课件）lesson34 磁场的性质

海大理学院教学裸件 大学物理学电子教案 磁场的性质 11-3磁通量磁场的高斯定律 11-4安培环路定理

大学物理学电子教案 海大理学院教学课件 磁场的性质 11-3 磁通量 磁场的高斯定律 11-4 安培环路定理

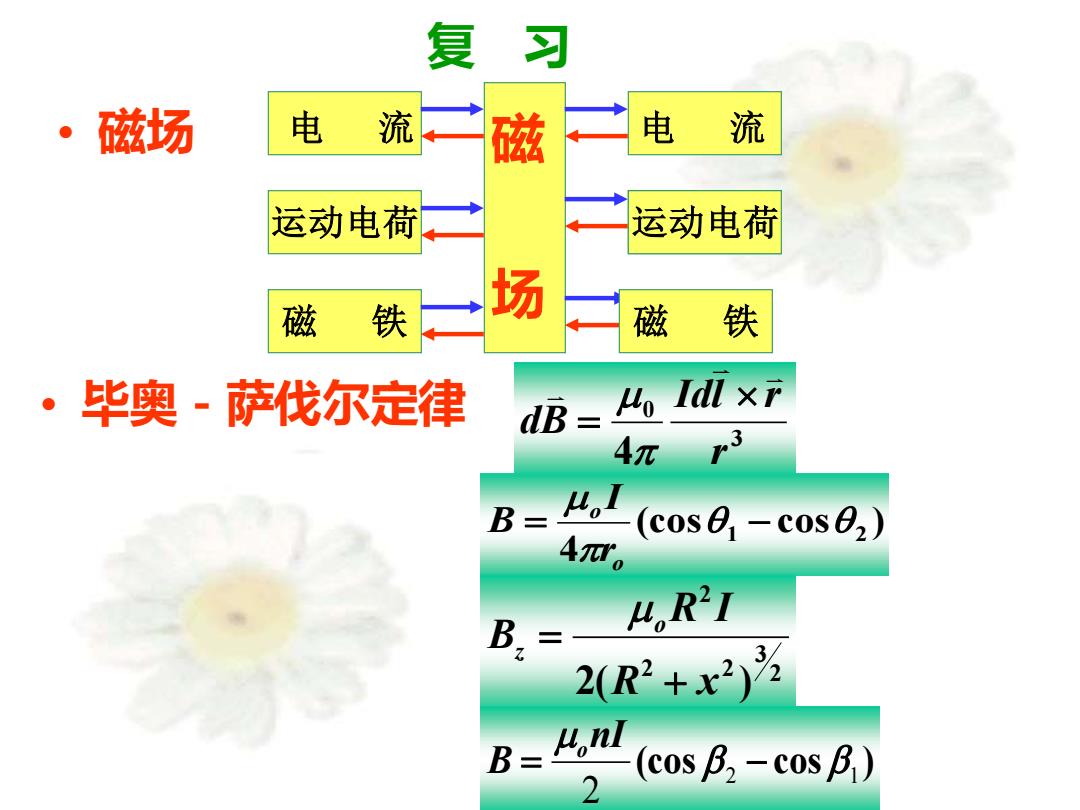
复习 磁场 电流一磁 二电流 运动电荷 运动电荷 磁 场 铁 磁铁 ·毕奥-萨伐尔定律 dB=Ho Idl x 4π B=(cos0-cose) AYo B.= 4,R27 2R2+x2)为 B=H.nl (cos B2 -cos B) 2

复 习 • 磁场 运动电荷 磁 铁 电 流 电 流 运动电荷 磁 铁 磁 场 3 0 4 r Idl r dB     =   (cos cos ) 4  1  2   = − o o r I B 2 3 2 2 2 2(R x ) R I B o z + =  (cos cos ) 2 1 2    = − nI B o • 毕奥－萨伐尔定律

三、运动电荷的磁场 dB=。,Ix示 B 4元 3 Idl nqvSdl Idl导线中运动电荷数目 dN=nSdl 所以运动电荷产生的磁场 dB 3_4。.nqSl×F 4。.q×F dN 4π nSdl.r3 4元 3 B= 4。,9×n 4π 1911年，俄国物理学家约飞最早提供实验验证

三、运动电荷的磁场 3 3 4 4 r qv r nSdl r nqvSdl r dN dB o o       =    =      Idl导线中运动电荷数目 dN=nSdl 所以运动电荷产生的磁场 Idl nqvSdl   = 3 4 r Idl r dB o     =    r  Idl  dB  3 4 r qv r B o     =    1911年，俄国物理学家约飞最早提供实验验证

例题：一半径为r的圆盘，其电荷面密度为σ，设 圆盘以角速度ω绕通过盘心垂直于盘面的轴转动， 求圆盘中心的磁感强度。 解法1：设圆盘带正电荷，绕轴O逆时针旋转， 在圆盘上取一半径分别为p与p+dp的细环带， 此环带的电量为dq=ods=o2πpdp,考虑到圆盘 以角速度o绕0轴旋转，周期为T=2m/o,于是 此环带上的圆电流为： 盘心O的磁感应强 度为 d= dq o2rplp 2π/0 _=oopdp B=goxp 己知圆电流在圆心处的磁感应强度为 J02 B=I/2R,其中I为圆电流，R为圆电流半 径，因此，圆盘转动时，圆电流在盘心O 的磁感应强度为： 磁感应强度的方向垂 直纸面向外。 20 2p

例题：一半径为r 的圆盘，其电荷面密度为σ，设 圆盘以角速度ω绕通过盘心垂直于盘面的轴转动， 求圆盘中心的磁感强度。 解法1：设圆盘带正电荷，绕轴O逆时针旋转， 在圆盘上取一半径分别为ρ与ρ+dρ的细环带， 此环带的电量为dq=σds=σ2πρdρ，考虑到圆盘 以角速度ω绕O轴旋转，周期为T=2π/ω，于是 此环带上的圆电流为：         d d T dq dI 2 / 2 = = = 已知圆电流在圆心处的磁感应强度为 B=μ0 I/2R，其中I为圆电流，R为圆电流半 径，因此，圆盘转动时，圆电流在盘心O 的磁感应强度为： 盘心O的磁感应强 度为           d d dI dB 2 2 2 0 0 0 = = = r B d r        0 0 0 2 1 2 = =  磁感应强度的方向垂 直纸面向外

解法2：取小微元dpd0 小微元所带的电荷为：dq=opdpd0 运动速度为=Qp，方向垂直于矢径 小微元在盘心0点产生在磁场为： dB=AP_cppd9p·p=1 3 4πp 4元 p uoaxpdo π 方向垂直于纸面向外，各个小微元在盘心处产生的磁场方向 都向外，积分得盘心处的磁感应强度为： B=玩4oan0=24oa

解法2：取小微元dρdθ 小微元所带的电荷为：dq=σρdρdθ 运动速度为v=ω ρ ，方向垂直于矢径 小微元在盘心O点产生在磁场为：                     d d dqv d d dB 3 0 0 3 0 4 1 4 4 =   = = 方向垂直于纸面向外，各个小微元在盘心处产生的磁场方向 都向外，积分得盘心处的磁感应强度为： B d d r r           0 0 2 0 0 2 1 4 1 = =  