
海大理学院表号裸件 大学物理学电子教案 静电场中的电介质2 9一5静电场的能量能量密度 9一6静电的应用 9一7电场的边界条件 9一8压电效应铁电体驻极体
大学物理学电子教案 海大理学院教学课件 静电场中的电介质2 9-5 静电场的能量 能量密度 9-6 静电的应用 9-7 电场的边界条件 9-8 压电效应 铁电体 驻极体

复习 静电场中的电介质 i=fo 电位移 D=50E+P=EE 电介质中的高斯定理 月D.s=g
复 习 •静电场中的电介质 r E E 0 = D E P r E = + = 0 D dS Q S = •电位移 •电介质中的高斯定理

9-5静电场的能量1 能量密度 电容器的电能 设在某时刻两极板之间的电势差为U, 此时若把+dg电荷从带负电的负极板 搬运到带正电的正极板,外力所作的 功为 dW Udg=1 dq 若使电容器的两极板分别带有士Q的电荷,则外力所作的功为 W- 2C 20w-cw2 电容器所储存的静电能 外力克服静电场力作功, 把非静电能转换为带电 W CU2 体系的静电能 2C1
9-5 静电场的能量 能量密度 一、电容器的电能 设在某时刻两极板之间的电势差为U, 此时若把+dq电荷从带负电的负极板 搬运到带正电的正极板,外力所作的 功为 E +dq + _ dq C q dW = Udq = 若使电容器的两极板分别带有±Q的电荷,则外力所作的功为 2 2 0 2 1 2 1 2 Q U CU C Q dq C q W Q = = = = 电容器所储存的静电能 2 2 2 1 2 CU C Q We = = 外力克服静电场力作功, 把非静电能转换为带电 体系的静电能

静电场的能量能量密度 1、静电场的能量 对于极板面积为S、极板间距为平板电容器,电场所 占的体积为Sd,电容器储存的静电能为 2 d 电容器所具有的能量与极板间电场E和D有关,E和D是极板 间每一点电场大小的物理量,所以能量与电场存在的空间有 关,电场携带了能量。 2、电场的能量密度 定义:单位体积内的能量 0。 对于任意电场,本结论都是成立的
二、静电场的能量 能量密度 1、静电场的能量 对于极板面积为S、极板间距为d平板电容器,电场所 占的体积为Sd,电容器储存的静电能为 (Ed) SE d d S We CU2 2 2 2 1 2 1 2 1 = = = 2、电场的能量密度 定义:单位体积内的能量 2 2 1 e = E 对于任意电场,本结论都是成立的。 电容器所具有的能量与极板间电场E和D有关,E和D是极板 间每一点电场大小的物理量,所以能量与电场存在的空间有 关,电场携带了能量
例1、球形电容器的内、外半径分别为R, 和R2,所带的电量为士9。若在两球之间 充满电容率为ε的电介质,问此电容器电 场的能量为多少。 解:若电容器两极板上电荷的分布是均匀的, 则测球壳间的电场是对称的。由高斯定理可求得 球壳间的电场强度的大小为 E= 电场总能量为 4r8r2 电场的能量密度为 w.=[ dr 2 32π2εr4 取半径为r厚为dr的球壳,其体 =0' 1 积为d=4πr2dr。所以此体积元内 8π8 R R, 的电场的能量为 dW。=o.dV= 42d= 32π2er4 8πr2
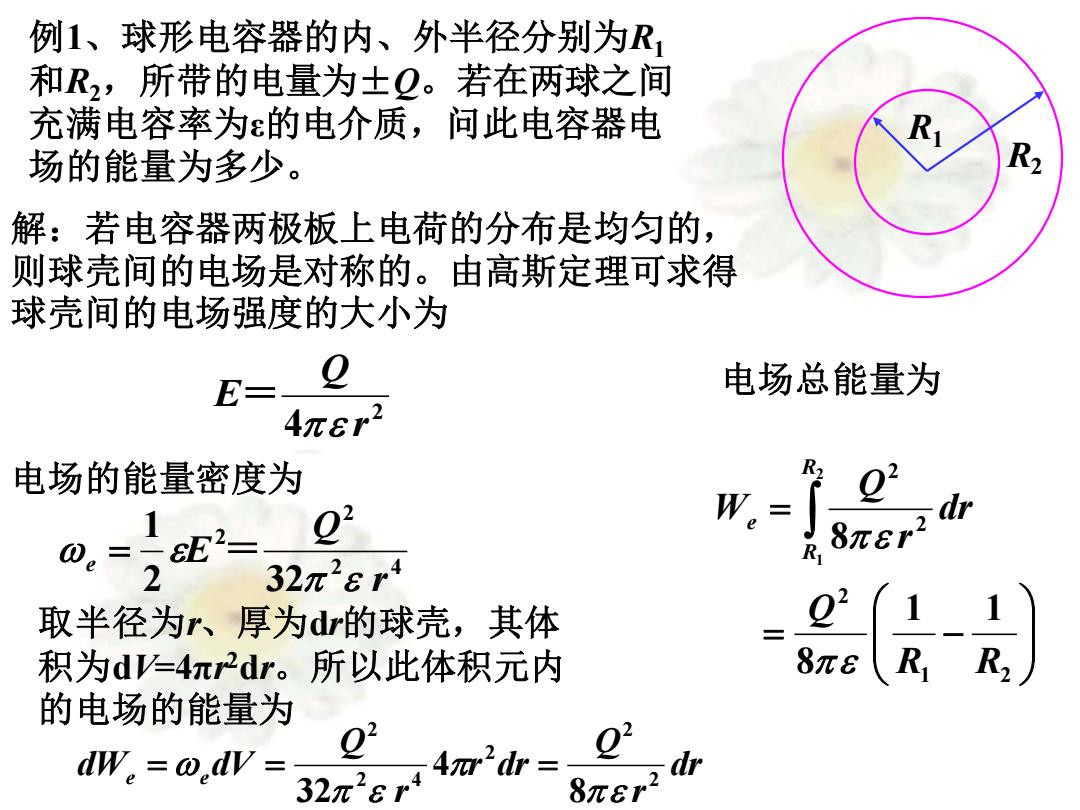
例1、球形电容器的内、外半径分别为R1 和R2,所带的电量为±Q。若在两球之间 充满电容率为ε的电介质,问此电容器电 场的能量为多少。 R1 R2 解:若电容器两极板上电荷的分布是均匀的, 则球壳间的电场是对称的。由高斯定理可求得 球壳间的电场强度的大小为 2 4 r Q E = 电场的能量密度为 2 4 2 2 2 32 1 r Q e E = = 取半径为r、厚为dr的球壳,其体 积为dV=4πr 2dr。所以此体积元内 的电场的能量为 dr r Q r dr r Q dWe e dV 2 2 2 2 4 2 8 4 32 = = = 电场总能量为 = − = 1 2 2 2 2 1 1 8 8 2 1 R R Q dr r Q W R R e