
海大理学院教学裸件 大学物理学电子教案 感生电动势、自感与互感 13-2动生电动势和感生电动势 (下花 13-3自感与互感 13-4RL电路
大学物理学电子教案 海大理学院教学课件 感生电动势、自感与互感 13-2 动生电动势和感生电动势(下) 13-3 自感与互感 13-4 RL电路

复习 电磁感应定律 ·电磁感应的基本现象 ·法拉第电磁感应定律 。1 楞次定律 ·动生电动势和感生电动势 ·动生电动势
复 习 • 电磁感应定律 • 电磁感应的基本现象 • 法拉第电磁感应定律 • 楞次定律 • 动生电动势和感生电动势 • 动生电动势
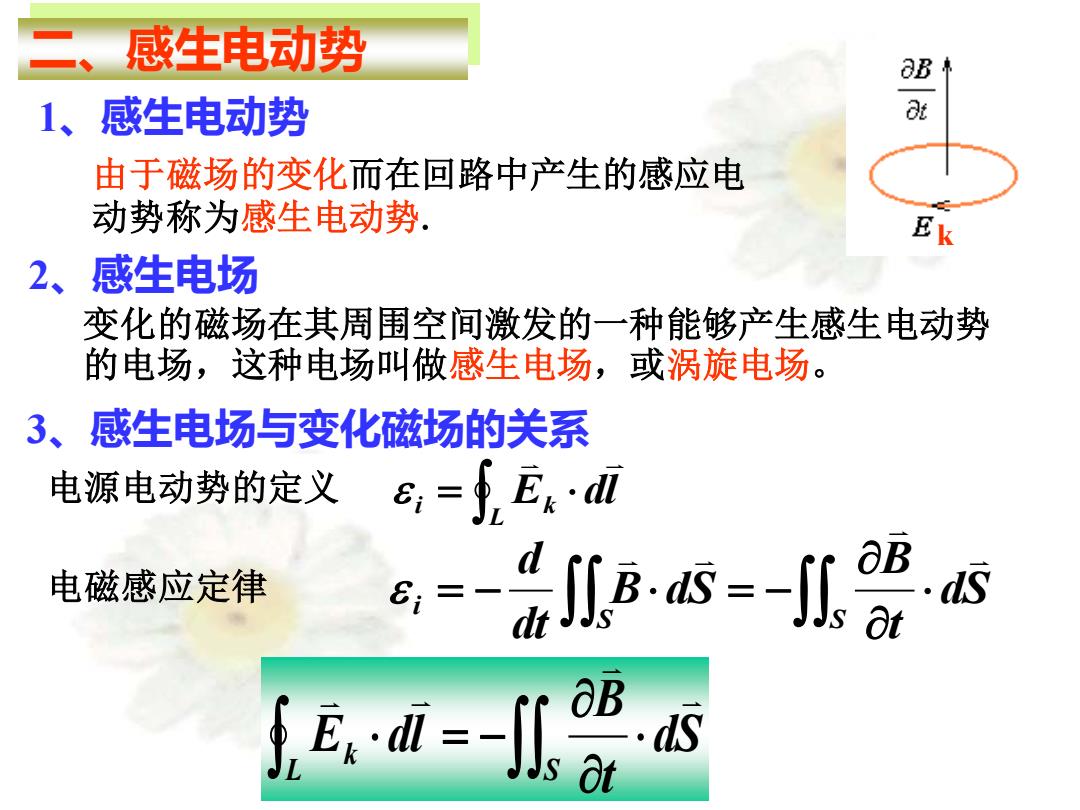
二、感生电动势 1、感生电动势 由于磁场的变化而在回路中产生的感应电 动势称为感生电动势. 2、感生电场 变化的磁场在其周围空间激发的一种能够产生感生电动势 的电场,这种电场叫做感生电场,或涡旋电场。 3、感生电场与变化磁场的关系 电源电动势的定义 e,=fEk·dl 电磁感应定律 话8s=-s Ra=-9内
二、感生电动势 由于磁场的变化而在回路中产生的感应电 动势称为感生电动势. 1、感生电动势 2、感生电场 变化的磁场在其周围空间激发的一种能够产生感生电动势 的电场,这种电场叫做感生电场,或涡旋电场。 3、感生电场与变化磁场的关系 = − = − S S i dS t B B dS dt d = L i k E dl 电源电动势的定义 电磁感应定律 dS t B E dl L S k = − k

4、说明: •感生电场的电场线是无头无尾的闭合曲线,所以又叫涡旋电场。 E面=八西 5B.l=八j ·感生电场和磁感应强度的变化连在一起。变化 的磁场和它所激发的感生电场,在方向上满足 反右手螺旋关系—左手螺旋关系。 感生电场与静电场相比 相同处: 不相同处: 对电荷都有作用力。 涡旋电场不是由电荷激发, 是由变化磁场激发。 若有导体存在都 涡旋电场电场线不是有头有尾, 能形成电流 是闭合曲线。 5、感生电动势的计算: e:=3 Ex'di dΦ 8:= dt
•感生电场的电场线是无头无尾的闭合曲线,所以又叫涡旋电场。 dS t B E dl L S k = − = L S B dl j dS 0 •感生电场和磁感应强度的变化连在一起。变化 的磁场和它所激发的感生电场,在方向上满足 反右手螺旋关系——左手螺旋关系。 •感生电场与静电场相比 相同处: 对电荷都有作用力。 若有导体存在都 能形成电流 不相同处: 涡旋电场不是由电荷激发, 是由变化磁场激发。 涡旋电场电场线不是有头有尾, 是闭合曲线。 4、说明: k 5、感生电动势的计算: = L i k E dl dt d i = −

例1.设空间有磁场存在的圆柱形区域的半径 为R=5cm,磁感应强度对时间的变化率为 dB/dt=0.2Ts,试计算离开轴线的距离等于 2cm、5cm及10cm处的涡旋电场。 解:如图所示,以为半径作一圆形闭合回路 L,根据磁场分布的轴对称性和感生电场的 电场线呈闭合曲线特点,可知回路上感生电 场的电场线处在垂直于轴线的平面内,它们 是以轴为圆心的一系列同心圆,同一同心圆 上任一点的感生电场的E大小相等,并且方 向必然与回路相切。于是沿L取E的线积分, 有: fE:i=E2知 Ek2=-π2 dB dt 若r<R,则Φ=Br2 r dB E=-恤=-a2B Ek 2 dt
例1.设空间有磁场存在的圆柱形区域的半径 为R=5cm,磁感应强度对时间的变化率为 dB/dt=0.2T/s,试计算离开轴线的距离r等于 2cm、5cm及10cm处的涡旋电场。 解:如图所示,以为半径r作一圆形闭合回路 L,根据磁场分布的轴对称性和感生电场的 电场线呈闭合曲线特点,可知回路上感生电 场的电场线处在垂直于轴线的平面内,它们 是以轴为圆心的一系列同心圆,同一同心圆 上任一点的感生电场的Ek大小相等,并且方 向必然与回路相切。于是沿L取Ek的线积分, 有: E dl E r k L k = 2 若r<R,则 2 = Br dt dB r dt d E dl L k 2 = − = - dt dB E r r k 2 2 = − dt r dB Ek 2 = −