
海大理学院教学裸件 大学物理学电子教案 波的衍射与干涉 15-3波的能量 15一4惠更斯原理波的衍射、反 射和折射 15一5波的干涉
大学物理学电子教案 海大理学院教学课件 波的衍射与干涉 15-3 波的能量 15-4 惠更斯原理 波的衍射、反 射和折射 15-5 波的干涉

复习 波动的基本概念 •横波和纵波 ·波长、波的周期和频率、波速 儿= 平面简谐波的波函数 y-Ac 波函数的物理意义
复 习 波动的基本概念 •横波和纵波 •波长、波的周期和频率、波速 = = T u •平面简谐波的波函数 = - + u x y Acos t •波函数的物理意义
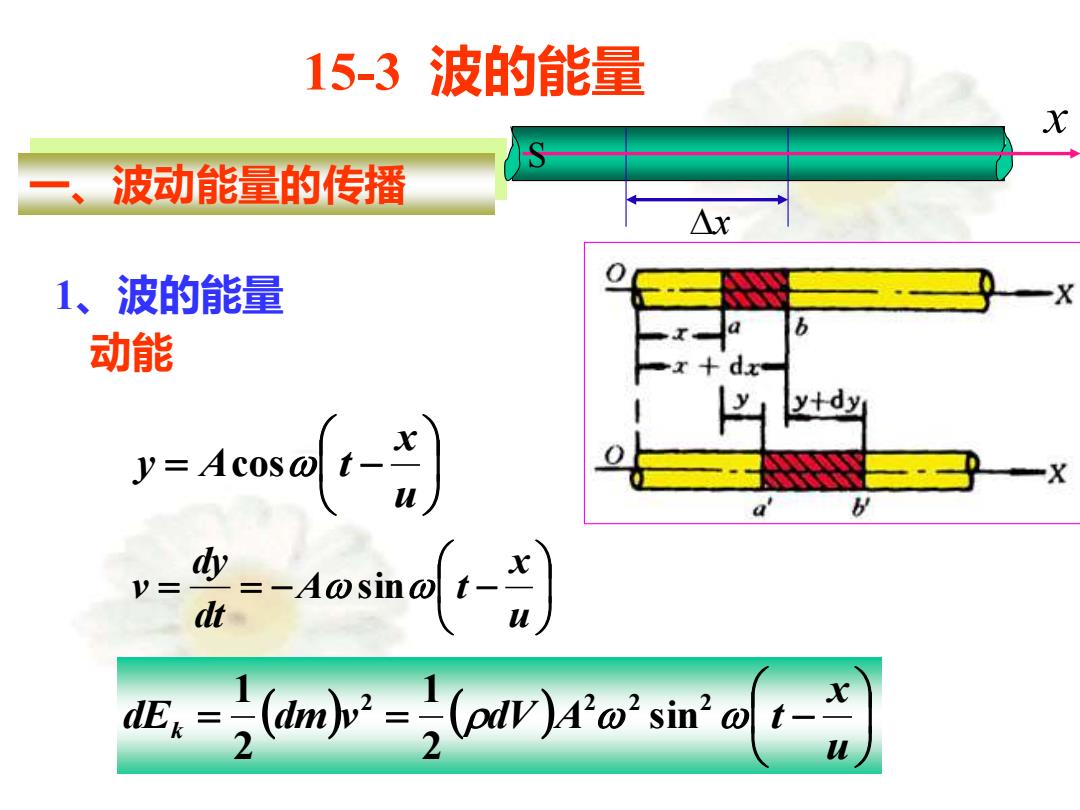
15-3 波的能量 波动能量的传播 △x 1、波的能量 动能 y+dy dE,=(dm)v=(odV)&o'sinot
15-3 波的能量 一、波动能量的传播 1、波的能量 动能 = − u x y Acos t = = − − u x A t dt dy v sin ( ) ( ) = = − u x dE dm v dV A t k 2 2 2 2 sin 2 1 2 1 x x S
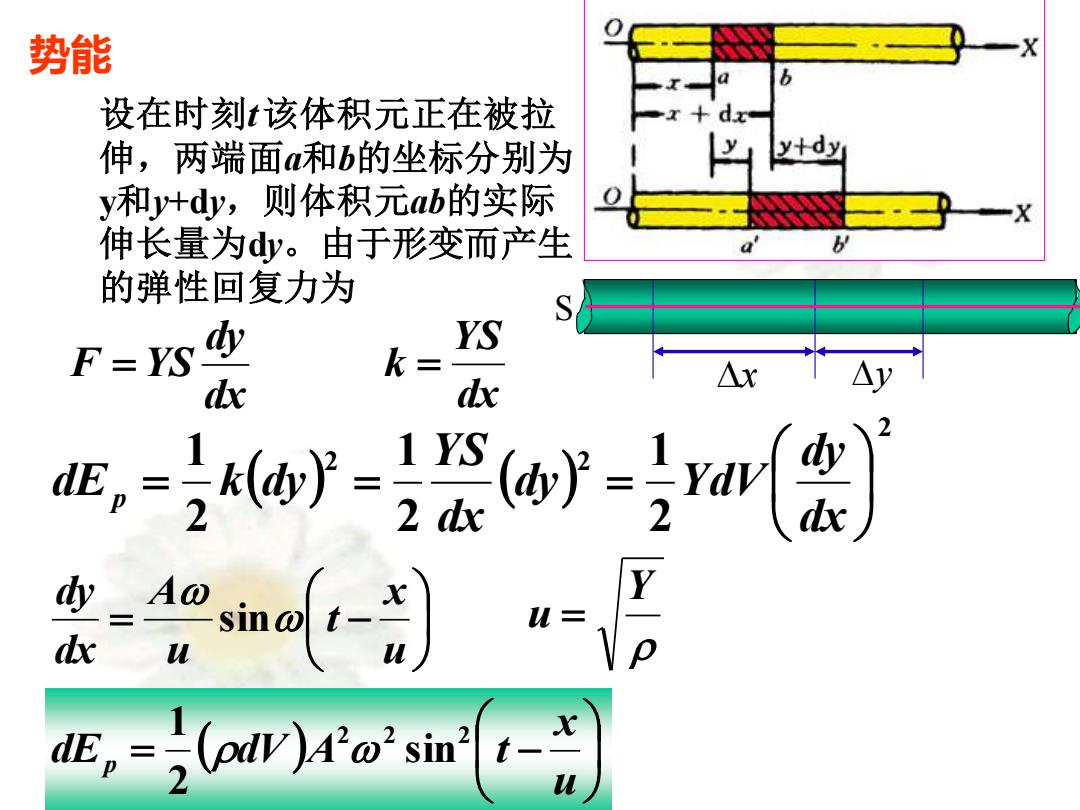
势能 设在时刻该体积元正在被拉 伸,两端面a和b的坐标分别为 y+dy y和y+dy,则体积元ab的实际 伸长量为dy。由于形变而产生 的弹性回复力为 S F=YS 西 YS k= dx d △y 2 2 dE,=,(oW))Ao2sin
势能 设在时刻t该体积元正在被拉 伸,两端面a和b的坐标分别为 y和y+dy,则体积元ab的实际 伸长量为dy。由于形变而产生 的弹性回复力为 dx dy F = YS dx YS k = ( ) ( ) 2 2 2 2 1 2 1 2 1 = = = dx dy dy YdV dx YS dE k dy p = − u x t u A dx dy sin Y u = ( ) = − u x dE dV A t p 2 2 2 sin 2 1 x y S
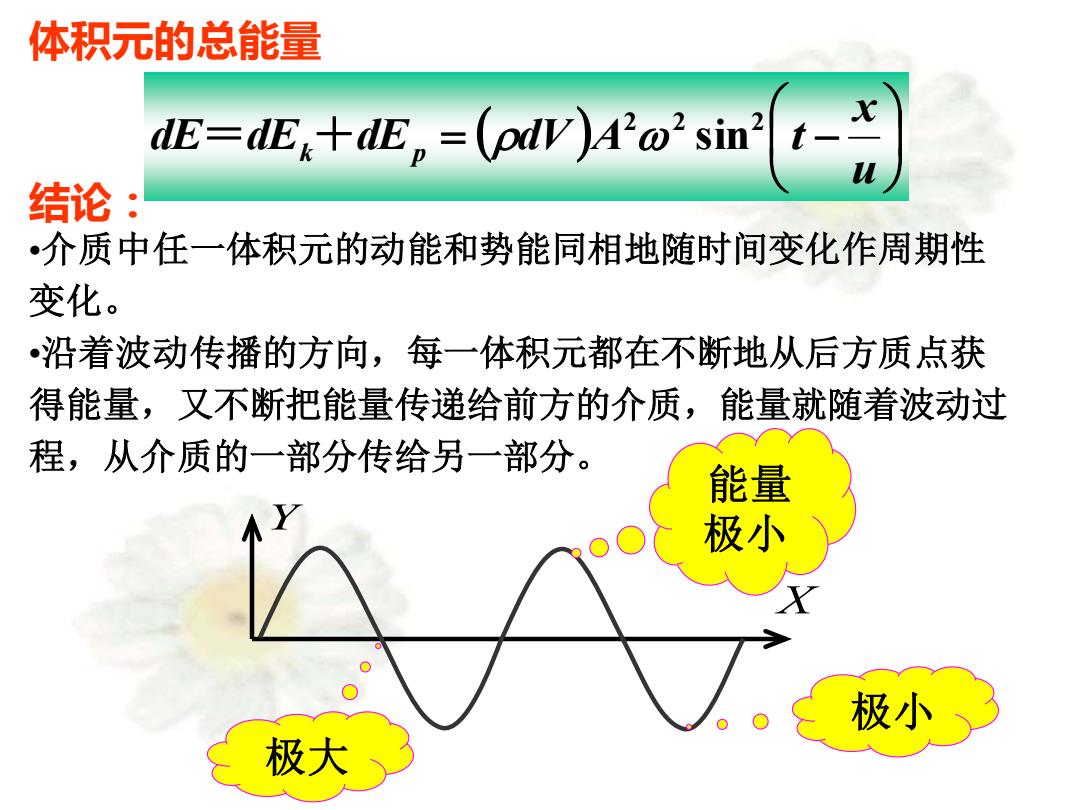
体积元的总能量 dE=dEx+dE,=(pdv)A'a2 sin2 结论 •介质中任一体积元的动能和势能同相地随时间变化作周期性 变化。 •沿着波动传播的方向,每一体积元都在不断地从后方质点获 得能量,又不断把能量传递给前方的介质,能量就随着波动过 程,从介质的一部分传给另一部分。 能量 极小 极小 极大
体积元的总能量 ( ) = − u x dE dE dE dV A t k p 2 2 2 = + sin 结论: •介质中任一体积元的动能和势能同相地随时间变化作周期性 变化。 •沿着波动传播的方向,每一体积元都在不断地从后方质点获 得能量,又不断把能量传递给前方的介质,能量就随着波动过 程,从介质的一部分传给另一部分。 X Y 极大 能量 极小 极小