
2、波的能量密度 定义:单位体积介质中的能量就是能量密度 花=pois-周 平均能量密度一一个周期内的能量密度的平均值 osiw)
2、波的能量密度 定义:单位体积介质中的能量就是能量密度 − u x A t dV dE w 2 2 2 = = sin 平均能量密度——一个周期内的能量密度的平均值 2 2 0 2 2 2 2 1 sin 1 A dt u x A t T w T = − =
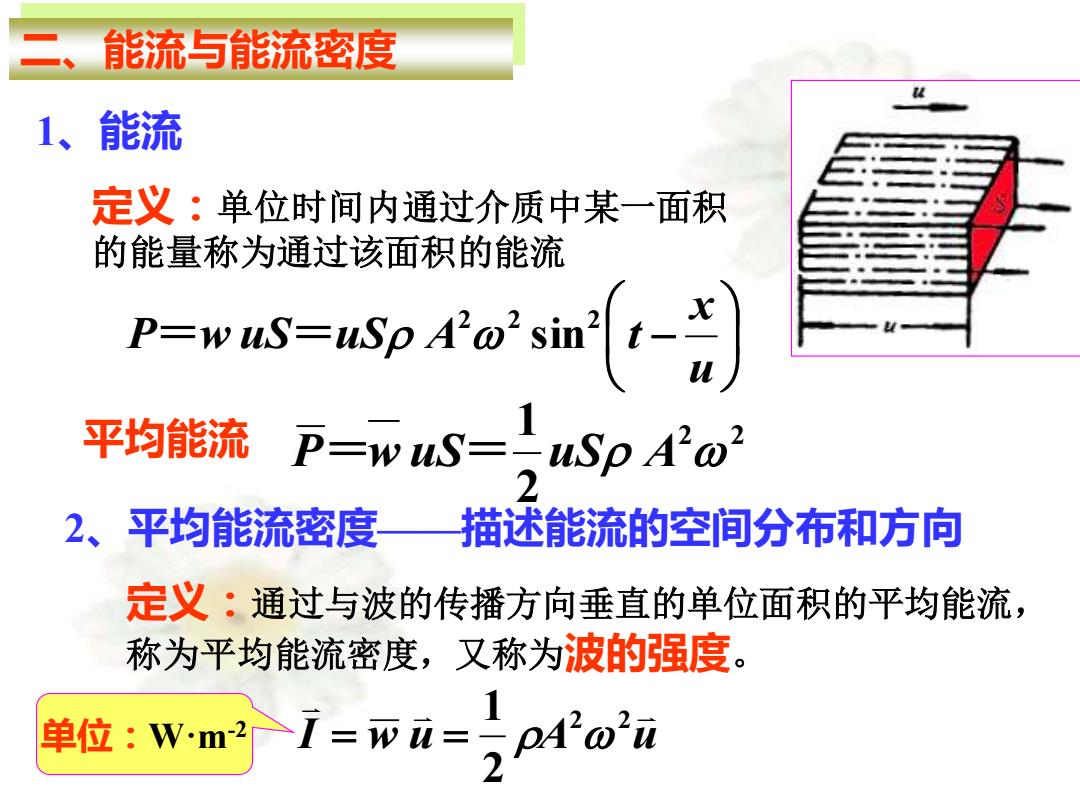
能流与能流密度 1、 能流 定义:单位时间内通过介质中某一面积 的能量称为通过该面积的能流 P=ww=ap4os气- 平均能流P=wS=。uSp A'a2 2、平均能流密度描述能流的空间分布和方向 定义:通过与波的传播方向垂直的单位面积的平均能流, 称为平均能流密度,又称为波的强度。 单位:Wm2 7=西三)212ω2z
二、能流与能流密度 1、能流 定义:单位时间内通过介质中某一面积 的能量称为通过该面积的能流 − u x P w uS uS A t 2 2 2 = = sin 平均能流 2 2 2 1 P=w uS= uS A 2、平均能流密度——描述能流的空间分布和方向 定义:通过与波的传播方向垂直的单位面积的平均能流, 称为平均能流密度,又称为波的强度。 I w u A u 2 2 2 1 单位:W·m-2 = =

例1、一球面波在均匀无吸收的介质中一波速u传播。在距离波 源r=1处质元的振幅为A。设波源振动的角频率为o,初相位 为零,试写出球面简谐波的表达式。 解:以点波源O以圆心作半径为和,的两 个球面,如图所示。由于介质不吸收波的 能量,因此,单位时间内通过球面的总平 均能量应该相等,即 41211=4m2212 An=A5 由于振动的相位随距离的增加而落后的 所以振幅与离波源的 关系,与平面波类似,球面简谐波的波 距离成反比。如果距 函数: 波源单位距离的振幅 A 为A,则距波源r处的 y=一 coso(t-- 振幅为A/r
1 r 2 r 由于振动的相位随距离的增加而落后的 关系,与平面波类似,球面简谐波的波 函数: cos ( ) u r t r A y = − 解:以点波源O以圆心作半径为r1和r2的两 个球面,如图所示。由于介质不吸收波的 能量,因此,单位时间内通过球面的总平 均能量应该相等,即 所以振幅与离波源的 距离成反比。如果距 波源单位距离的振幅 为A,则距波源r处的 振幅为A/ r 例1、一球面波在均匀无吸收的介质中一波速u传播。在距离波 源r1=1m处质元的振幅为A。设波源振动的角频率为ω ,初相位 为零,试写出球面简谐波的表达式。 2 2 1 2 2 4r1 I = 4r I I A u 2 1 2 1 2 1 = I A u 2 2 2 2 2 1 = 1 1 2 2 A r = A r