
海大理学院放学裸件 大学物理学电子教案 简谐运动的应用 14-6简谐运动的合成 14-7阻尼振动、受迫振动、共振
大学物理学电子教案 海大理学院教学课件 简谐运动的应用 14-6 简谐运动的合成 14-7 阻尼振动、受迫振动、共振

复习 单摆和复摆 简谐运动的能量 E=m'o-
复习 单摆和复摆 简谐运动的能量 2 2 2 2 1 2 1 E= mA = kA

14-6简谐运动的合成 两个同方向同频率简谐运动的合成 某质点同时参与两个同频率且在同一条直线上的简谐运动 七1=Ac0s(ot+p,) Asino=A sing+A2 sinp2 x2 A2 cos(@t+o2) Acoso=A coso+42 cos2 合振动 x=x+x x=Acosocos@t-Asinosin@t =Acos(@t+o) 1、应用解析法 x=x+x2 A=+2+244 cos(2-) =A cos(@t+o:HA cos(@t+oz) =(A coso:+A2 cosp2)cos@t g0= A sinp+A2 sinpz -(A sing+A,sing,)sin@t A coso+4 cos
14-6 简谐运动的合成 一、两个同方向同频率简谐运动的合成 某质点同时参与两个同频率且在同一条直线上的简谐运动 ( ) ( ) 2 2 2 1 1 1 cos cos = + = + x A t x A t 合振动 x = x1 + x2 1、应用解析法 ( ) ( ) ( ) (A A ) t A A t A t A t x x x sin sin sin cos cos cos cos cos 1 1 2 2 1 1 2 2 1 1 2 2 1 2 − + = + + + = + = + 1 1 2 2 1 1 2 2 cos cos cos sin sin sin A A A A A A = + = + ( ) + − A t x A t A t cos cos cos sin sin = = 2 cos( ) 1 2 2 1 2 2 2 A = A1 + A + A A − 1 1 2 2 1 1 2 2 cos cos sin sin A A A A tg + + = 令
2、应用旋转矢量法 合成振动 是简谐运动 A sin p2 D A sin AC0Sp1A2c0sp≤ X 演示 x=Acos(@t+o) A=A2+A2+2442 cos(o2-g) A sin+42 sin t8⑩= A coso+42 cosp2
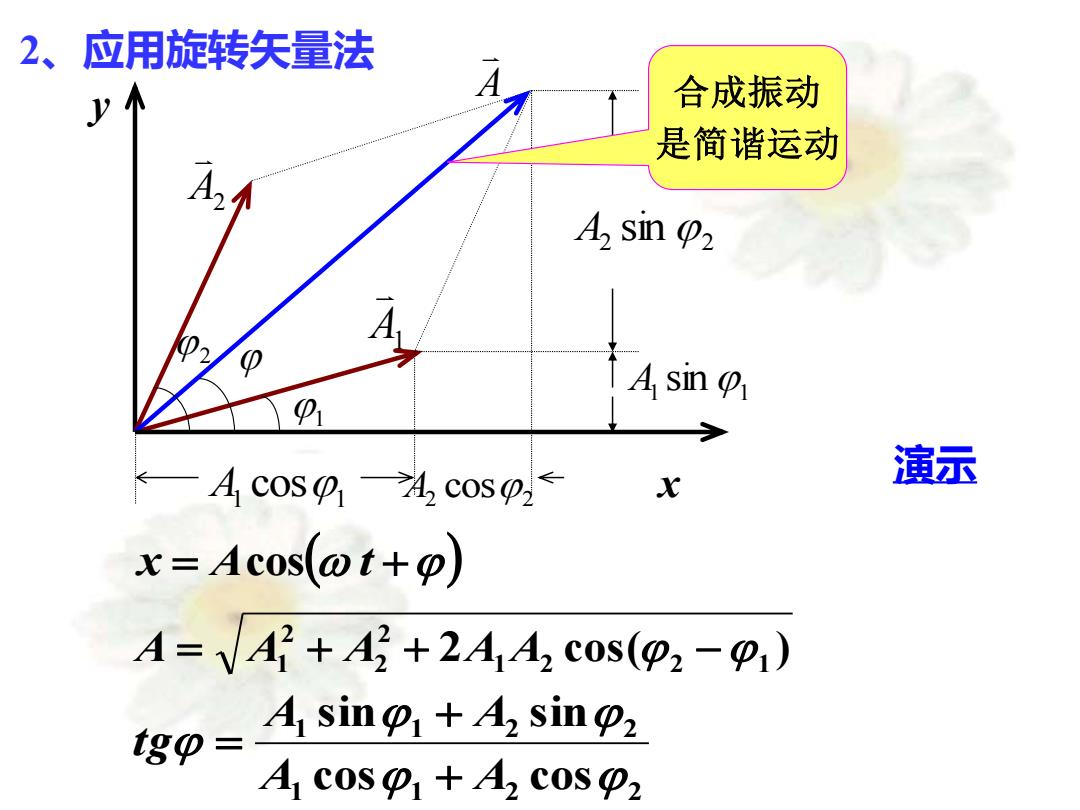
2、应用旋转矢量法 A2 A A1 2 1 x y 1 1 A cos 2 2 A cos 1 1 A sin 2 2 A sin 2 cos( ) 1 2 2 1 2 2 2 A = A1 + A + A A − 1 1 2 2 1 1 2 2 cos cos sin sin A A A A t g + + = 合成振动 是简谐运动 x = Acos( t +) 演示

3、讨论 情况1 P2-P1=±2kπ k=0,1,2,… A=A1十A2 合振幅最大 当A1=A称为干涉相长A=2A 情况2 92-91=±(2k-1)π k=1,2,3, A A=A1一A2合振幅最小 当A1=A,称为干涉相消A=0 情况3:一般情况 P2-91≠kπ A21 4-4kA<4+44
3、讨论 2 −1 = 2k k = 0,1,2, A= A1 + A2 合振幅最大 A2 A A1 情况1 当 A1 = A2 称为干涉相长 A= 2A1 A2 A A1 A1 A2 A | | | | A1 − A2 A A1 + A2 2 −1 k 情况2 2 −1 = (2k −1) k = 1,2,3, A = A1 − A2 合振幅最小 当 A1 = A2 称为干涉相消 A= 0 情况3:一般情况