
腔内体源J=0 由方程(3.2.52)得: u登+-m亦nEaa 收+=出H 而面,有女卷 将其代入上式,有 dg+kr。-eR,d+》RO。i drm -oE+m=-j0eR.0+》RQ @mM -02+0+0(-1+=0 +o01--2=0
将其代入上式,有 腔内体源J=0 S’=0 由方程(3.2.52)得: ' 2 2 ' 2 2 2 2 2 ( ) ( ) m m m m m m m V S S m m m m m m m m S S d r d k r k J E dv n H E ds n E H ds dt dt d r dr d k r Z H H ds Z H ds dt dt dt 2 m m S m m H ds R Q 而由前面,有 2 2 2 =- (1 ) m m m m m m m m d r dr k r R j dt R Q dt 2 2 2 2 + ( 1 ) 0 (1 ) 0 m m m m m m j Q j Q 2 2 (1 ) m m m m m j R j R Q m j t m m r B e

→ 0= 20m 生®心园} 20m 因m>1→ 为得正频率,故上式“±”中只取“+”号: →0=-石)12- 腔壁损耗,使得第m次模式的谐振角频率下降了一个 )因子,并有衰减常数
因 腔壁损耗,使得第m次模式的谐振角频率下降了一个 因子,并有衰减常数 2 (1 ) 2 2 4 m m m m m m j j Q Q Q 1 Qm 为得正频率,故上式“ ”中只取“+”号: 1 1 (1 ) (1 ) 2 2 2 m m m m m j Q Q Q 1 (1 ) 2Qm 1 (1 ) 2 2 m m m j Q Q
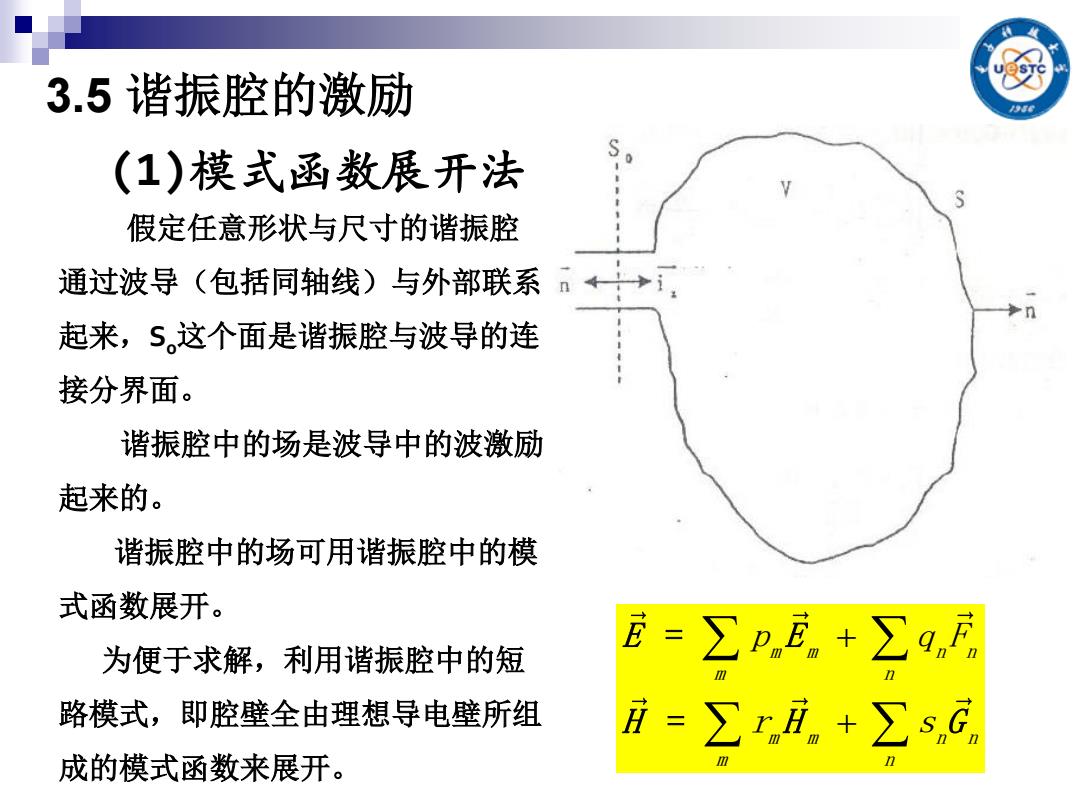
3.5谐振腔的激励 (1)模式函数展开法 假定任意形状与尺寸的谐振腔 通过波导(包括同轴线)与外部联系 起来,S,这个面是谐振腔与波导的连 接分界面。 谐振腔中的场是波导中的波激励 起来的。 谐振腔中的场可用谐振腔中的模 式函数展开。 为便于求解,利用谐振腔中的短 E=∑pE。+∑gF 路模式,即腔壁全由理想导电壁所组 月=∑r五。+∑sG 成的模式函数来展开
3.5 谐振腔的激励 假定任意形状与尺寸的谐振腔 通过波导(包括同轴线)与外部联系 起来,S0这个面是谐振腔与波导的连 接分界面。 谐振腔中的场是波导中的波激励 起来的。 谐振腔中的场可用谐振腔中的模 式函数展开。 为便于求解,利用谐振腔中的短 路模式,即腔壁全由理想导电壁所组 成的模式函数来展开。 (1)模式函数展开法 m m n n m n m m n n m n p q F r s = = E E H H G

E=∑p,E。+∑9方 腔中的场可展开为月=∑,i。+∑G。 其中E、i。、F,和G为短路模式函数。 在谐振腔的入口So面上,电场的切向 分量是由外部的波导场激发起来,并为已知。 S面上的波导场可用波导中正规波型电场的横向分量来展开。 令E,m表示波导中第n次波型的横向电场, 丑n表示第n次波型的横向磁场, Em、i是正交归一化场,它们满足
腔中的场可展开为 在谐振腔的入口S0面上,电场的切向 分量是由外部的波导场激发起来,并为已知。 S0面上的波导场可用波导中正规波型电场的横向分量来展开。 a a b b a b a a b b a b E p E q F H r H s G 其中E H F G a a b b 、 、 和 为短路模式函数。 tn tn tn tn E n H n E H 令 表示波导中第 次波型的横向电场, 表示第 次波型的横向磁场, 、 是正交归一化场,它们满足

i.×En/in=Zm =0, m≠n ∬in·Imds=dn→ S =1, m=n rEn·Endk=dnZm So 其中Z为第n次波型的波阻抗 v人会 对7波乙-臣3
=0, m≠n =1, m=n z tn tn on i E H Z 其中Z n on 为第 次波型的波阻抗 0 on g TM Z 对 波 0 0 2 tn tm mn S tn tm mn om S H H ds E E ds Z 0 0 g TE Z n 对 波