电子科技大学：《铁磁学》课程教学资源（课件讲稿）第五章 自旋波理论

§5.2自旋波的半经典理论 自旋S在磁场H中的Hamilton为： H=-u.H=-yhS.H (1) 如H∥Z轴，即H(0,0,H)则 H=-yhS.Hz(y:旋磁比) (2) 无阻尼时自旋在磁场H作用下的运动方程为： =s×i.(3③) dt 考虑一简单的一维无穷链，每个格点有相同的自旋§，相邻 格点之间存在交换作用（A>0),则第个格点交换作用 Hamilton:

§5.2自旋波的半经典理论 自旋S在磁场H中的Hamilton为： 如 轴，即 则 无阻尼时自旋在磁场H作用下的运动方程为： 考虑一简单的一维无穷链，每个格点有相同的自旋 ，相邻 格点之间存在交换作用（A>0），则第n个格点交换作用 Hamilton: S H......(3) dt dS      H H S H (1)            H // Z  H(0,0,H ) z  H S H ( : ( )   Z Z  旋磁比） ２   S 

Hn=-2ASn·∑Sn0 =-2ASn[Sn1+Sn-].(4) 比较（2)、（4)两式 用等效场H替代相邻格点自旋的交换作用 风，-6+815 (5)代入(3)： =5n×H dt 21s,×⑤+S.(6)

      1 1 2  n n  H n AS S  2 [ ]......(4) 1  1    ASn Sn Sn    比较（2）、（4）两式 用等效场Heff替代相邻格点自旋的交换作用 （5）代入（3）： ( )......(5) 2 eff  n1  n1 S S A H      n eff n S H dt dS      ( )......(6) 2  n  n1  n1 S S S A    

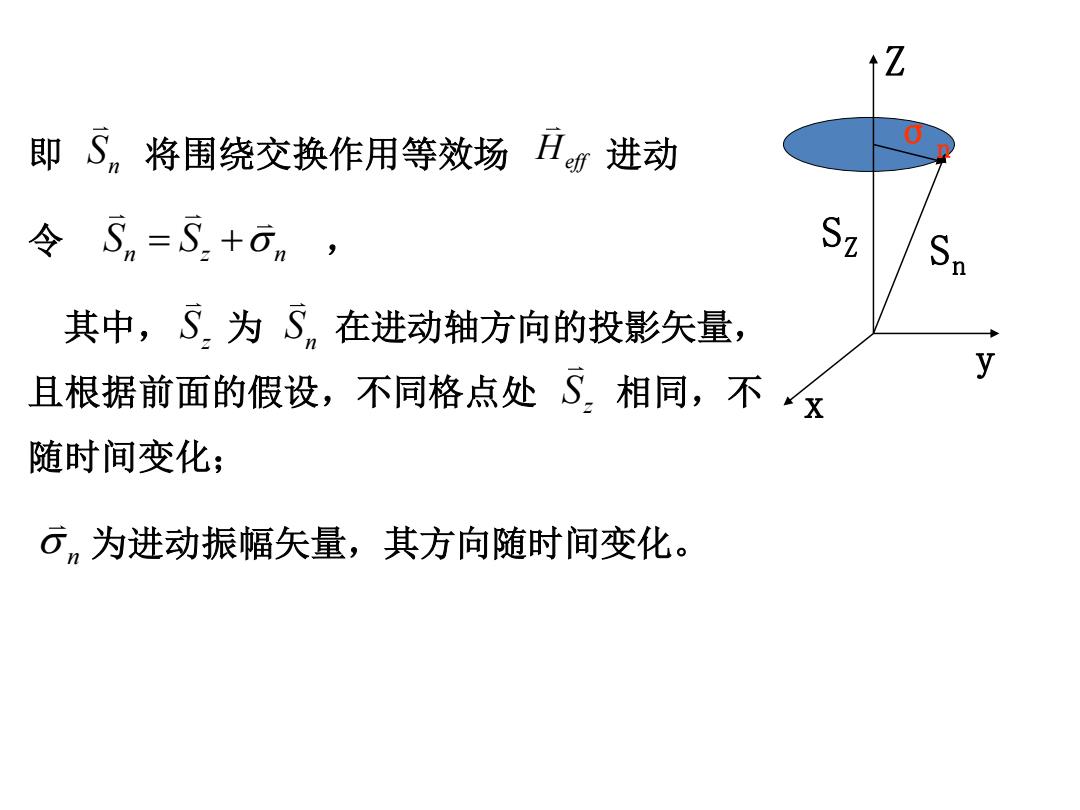
Z 即S,将围绕交换作用等效场H进动 0 令Sn=5.+6m, Sz Sn 其中，S为Sn 在进动轴方向的投影矢量， 且根据前面的假设，不同格点处S相同，不父 y 随时间变化； 云，为进动振幅矢量，其方向随时间变化

即 将围绕交换作用等效场 进动 令 ， 其中， 为 在进动轴方向的投影矢量， 且根据前面的假设，不同格点处 相同，不 随时间变化； 为进动振幅矢量，其方向随时间变化。 n S Heff n z n S S    n z S σ n SZ Sn Z x y n S z S

.自旋S,在交换作用等效场下的运动方程(P2s5): do= 24 2(S+6n)×(2S+6n+1+m-1) dt 如振幅很小，即ō<S时，略去二次以上项得线性方程： hdG=245.x(G41-2Gn+6-(7) dt (分量形式见P2ss) 如令o*=O+io,，则写成标量方程： ih80=-24S.(oi1-2o+o）(8) Ot 可取所有整数值，o0个形式相同的联立线性齐次方程

如振幅很小，即 时，略去二次以上项得线性方程： (分量形式见P255) 如令 ，则写成标量方程： ∴ 1 1 2 ( ) (2 ) n z n z n n d A S S dt            z   S 2 ( 2 )......(7)  z  n1  n  n1 n AS dt d          x y   i    2 ( 2 )......(8) 1 1             z n n n n AS t i      自旋 在交换作用等效场下的运动方程（P255 Sn )： n可取所有整数值，∞个形式相同的联立线性齐次方程

其解应当具有如下形式： ei(nka--o）. (9) a为相邻格点的间距，(9)代入（⑧）中 h0=84S.5m(9l0) →一维铁磁链的自旋波色散关系 如共有N个格点，则可以有N个k 的取值，即可以有N个波长不同 8AS/h 的自旋波存在。k的取值决定于 边界条件，在周期性边界条件下 ka -π 元

其解应当具有如下形式： ~ ......(9) i(nka t) n e     a为相邻格点的间距，(9)代入(8)中 ⇒一维铁磁链的自旋波色散关系 )......(10) 2 8 ( 2 k a   ASz Sin 如共有N个格点，则可以有N个k 的取值，即可以有N个波长不同 的自旋波存在。k的取值决定于 边界条件，在周期性边界条件下   n n Na     ω -π π 8 / AS ka