
代入(8)式有: =2mch'(L+12)2(n。+1)=(n。+1(64.6m) 3.The Huckel MO method Ha-H () H (g,=ep (12) -2f (13) 由线性变分法有:
代入(8)式有: 1 2 1 2 2 ( ) ( 1) ( 1)(64.6 ) m ch l l n n nm e c c − = + + = + 3 . The Huckel MO method ^ ^ ( ) eff i n H H i = (11) 1 c ri i r r n c f = = ^ ( ) eff i i i H i = e (12) (13) 由线性变分法有:

2H-s-e)c.1=0=1,23…n (14 久期方程 det H-s,e,=0 (15) 积分 H=∫fr)H)f),≡a (16) Hf(H()f (i)dv,=B for C &C,bonded =0 for CC,not bonded together (17 sn=∫f,0f,0)本=δ (18)
1 [( ) ] 0 c eff rs rs i si s n H sec = − = r=1,2,3,….nc (14) 久期方程: det | | 0 eff H S e rs rs i − = (15) 积分 * ( ) ( ) ( ) eff eff H f i H i f i dv rr r r i = ^ * ( ) ( ) ( ) eff eff i rs r r H H = f f i i i dv for Cr & Cs bonded (16) 0 eff H rs = for Cr & Cs not bonded together * ( ) ( ) i rs rs r s f f i i dv s = = (17) (18)

f≡C,2p. (19) 归一化条件(normalization condition) leaf =1 (20) 4.Conjugated Chain Molecules 1234n C-C-C-C..C (21)
2 r r f C p 归一化条件(normalization condition ) (19) 2 1 c ri r s n c = = (20) 4. Conjugated Chain Molecules 1 2 3 4 ... n c c c c c −−− (21)
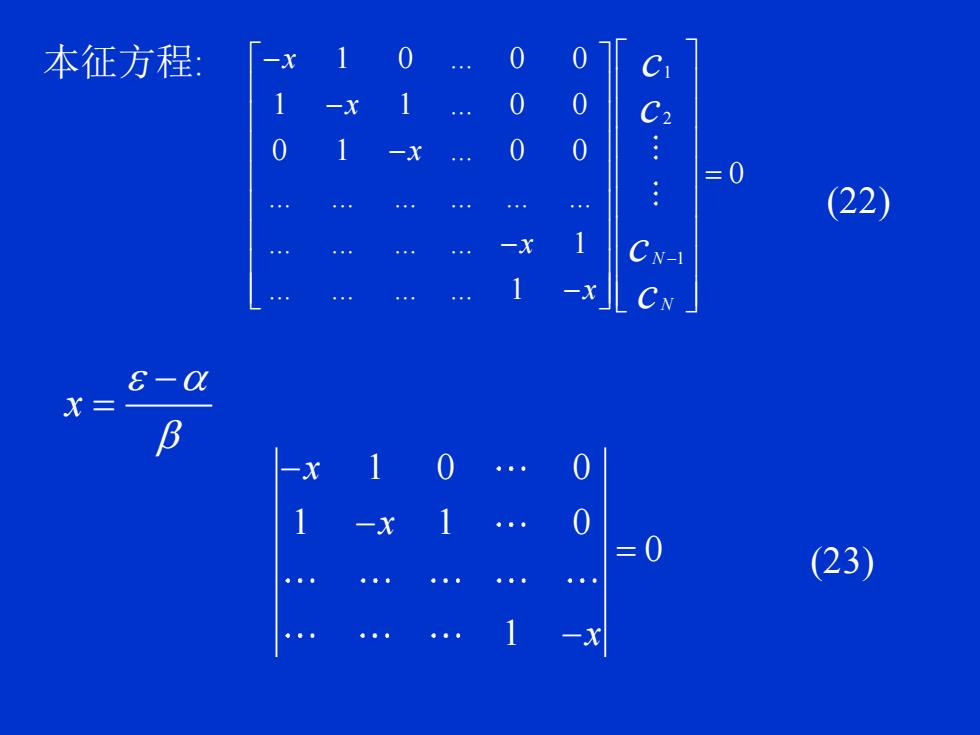
本征方程 0 C 1 0 0 一X 0 .: (22) CN- CN 8-Q X= 一X 0 (23)
本征方程: 1 2 1 1 0 ... 0 0 1 1 ... 0 0 0 1 ... 0 0 0 ... ... ... ... ... ... ... ... ... ... 1 ... ... ... ... 1 N N x x x x x c c c c − − − − = − − (22) x − = 1 0 0 1 1 0 0 1 x x x − − = − (23)

由行列式理论有 Ek=a+xB kπ (24) X=2cos N+1 k=1,2,3,,N 2 kuπ CN+1 in k=1,2,3,,N N+1 u=1,2,3,,N (25) 123 4 例子:丁二烯 H,C=C-C=CH, 2π X=2cos π X2=2cos 5 (26) 3π An X;=2cos X=2cos 5 5
由行列式理论有: k = + k 2cos 1 k k N x = + k=1, 2, 3, …, N (24) 2 sin 1 1 uk ku N N c = + + k=1, 2, 3, …, N u=1, 2, 3, …, N (25) 例子:丁二烯 1 2 3 4 H C C C C H 2 2 = − = 1 2cos 5 x = 3 3 2cos 5 x = 2 2 2cos 5 x = 4 4 2cos 5 x = (26)