
4.3.3AR(2)的方差、自协方差与自相关函数 由 y=C+C必1y-1+C2y-2+8, c=u(1-01-02) 可得 y,=I(1-01-02)+C%1y,-1+C2y-2+8
4.3.3 AR(2)的方差、自协方差与自相关函数 1 1 2 2 1 2 1 2 1 1 2 2 (1 ) (1 ) t t t t t t t t y c y y c y y y − − − − = + + + = − − = − − + + + 由 可得

并进而整理得 y,-u=(y,-1-4)+02(y,-2-4)+E, 两侧同乘以y,-4,然后取期望,得 Y)=01Yj-1+02Yj-2 根据自相关函数的定义,得关系式 P,=O1Pi-1+02Pj-2
1 1 2 2 1 1 2 2 1 1 2 2 ( ) ( ) , t t t t t j j j j j j j y y y y − − − − − − − − = − + − + − = + = + 并进而整理得 两侧同乘以 然后取期望,得 根据自相关函数的定义,得关系式

因此, p=a1po+a2p P2=ap+a2Po 又因为自相关函数具有以下性质 P=P’P=0=1 可得自相关函数在前2期的解析表达式 1-02 a-a3+&2 P2= 1-02
因此, 又因为自相关函数具有以下性质 可得自相关函数在前2期的解析表达式 1 1 0 2 1 2 1 1 2 0 = + − = + 0 0 0 1 j j = = = − , 1 1 2 2 2 1 2 2 2 2 1 1 = − − + = −

进而可推导出平稳AR(2)模型的 方差解析表达式: (1-a2) (1+a2)[(1-o2)-02]
进而可推导出平稳AR(2)模型的 方差解析表达式: 2 2 0 2 2 2 2 1 (1 ) (1 )[(1 ) ] − = + − −
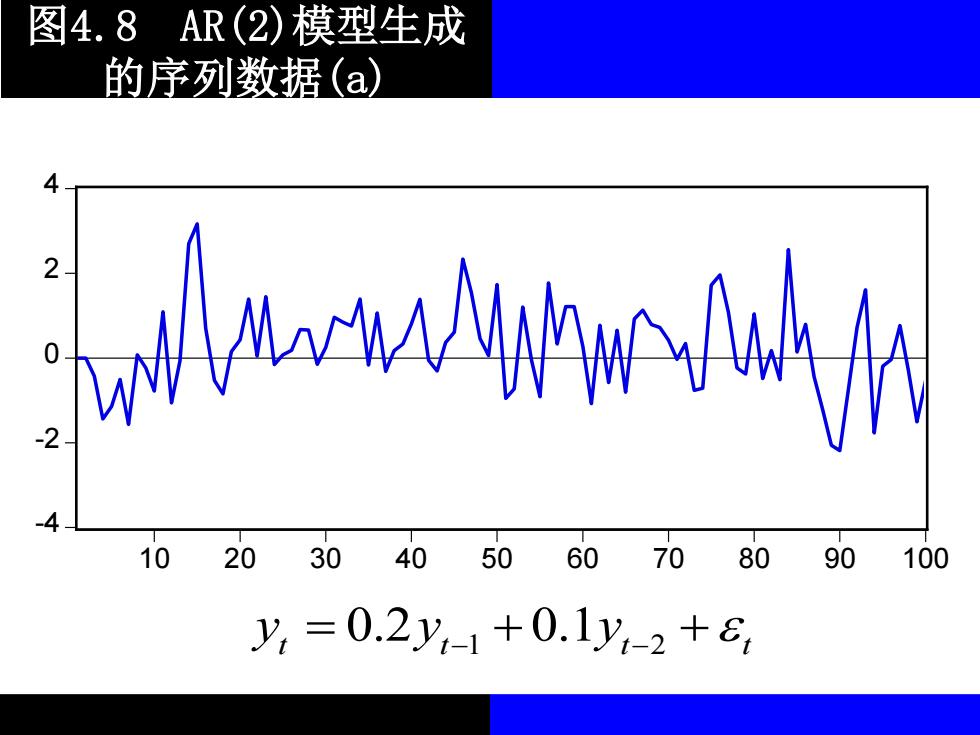
图4.8AR(2)模型生成 的序列数据(a) 44N山的 102030 4050 6070 8090100 y,=0.2y,-1+0.1y,-2+e
图4.8 AR(2)模型生成 的序列数据(a) -4 -2 0 2 4 10 20 30 40 50 60 70 80 90 100 t t t t 0.2 0.1 1 2 y y y = + + − −