
13.3 门限模型 门限模型的核心不涉及概率转移矩 阵,而是根据设定的门限,来分析模型 在不同区制的变化。在门限模型中,区 制的变化可以体现在模型在两个不同状 态下的变化,也可以是平滑性的变化。 一般以自回归模型为研究对象,所以前 者对应的是门限自回归模型,而后者对 应的是平滑自回归模型
13.3 门限模型 门限模型的核心不涉及概率转移矩 阵,而是根据设定的门限,来分析模型 在不同区制的变化。在门限模型中,区 制的变化可以体现在模型在两个不同状 态下的变化,也可以是平滑性的变化。 一般以自回归模型为研究对象,所以前 者对应的是门限自回归模型,而后者对 应的是平滑自回归模型

13.3.1基本的门限模型 假设对于一个AR(1)模型,如果其 均值在某个时刻发生变化,这种情况就 是门限模型的一种。如图11-2所示,对 于一个样本为T的y,序列,在d时刻之前 均值为,而在d时刻后,其均值跳跃 到41
13.3.1 基本的门限模型 假设对于一个AR(1)模型,如果其 均值在某个时刻发生变化,这种情况就 是门限模型的一种。如图11-2所示,对 于一个样本为T的 序列,在d时刻之前 均值为 ,而在d时刻后,其均值跳跃 到 。 t y 0 1

这样我们可以把AR(1)模型写成: y,-4=4(y-1-4w)+6,S=0,1 更一般地,TAR模型可以写成如下形式: y=C+9以t+0p-p+,,=0,1
这样我们可以把AR(1)模型写成: 更一般地,TAR模型可以写成如下形式: 1 1 ( ) , 0,1 t st t st t t y y s − − = − + = , ,1 1 , 0,1 t t t t s s t s p t p t t y c y y s − − = + + + + =
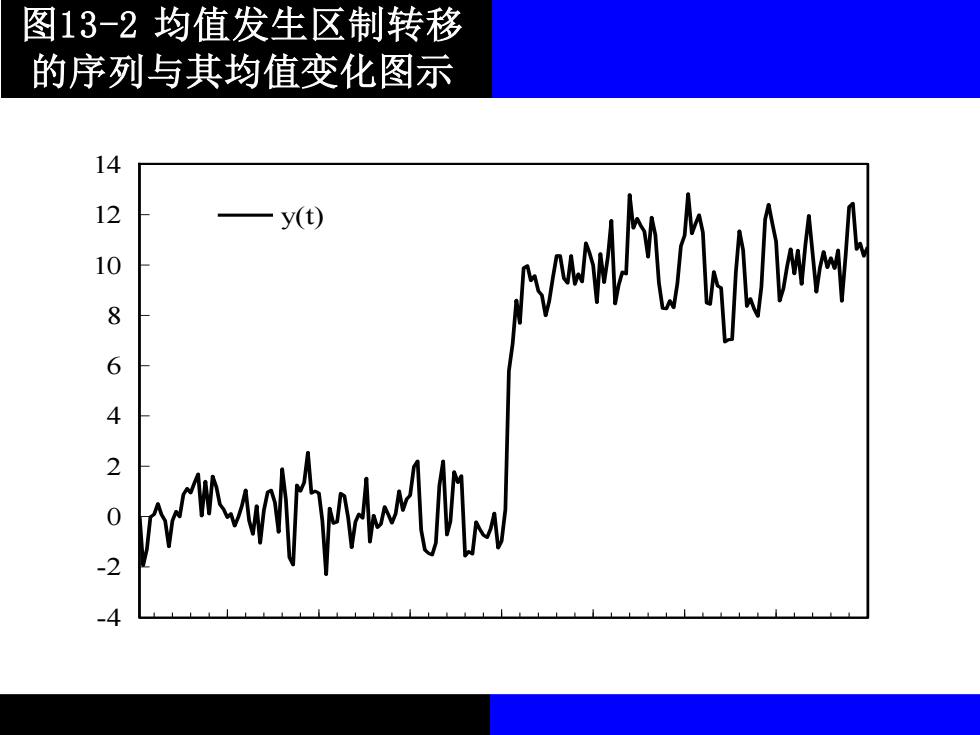
图13-2均值发生区制转移 的序列与其均值变化图示 14 12 y(t) 8 M wiwb
图13-2 均值发生区制转移 的序列与其均值变化图示 -4 -2 0 2 4 6 8 10 12 14 y(t)
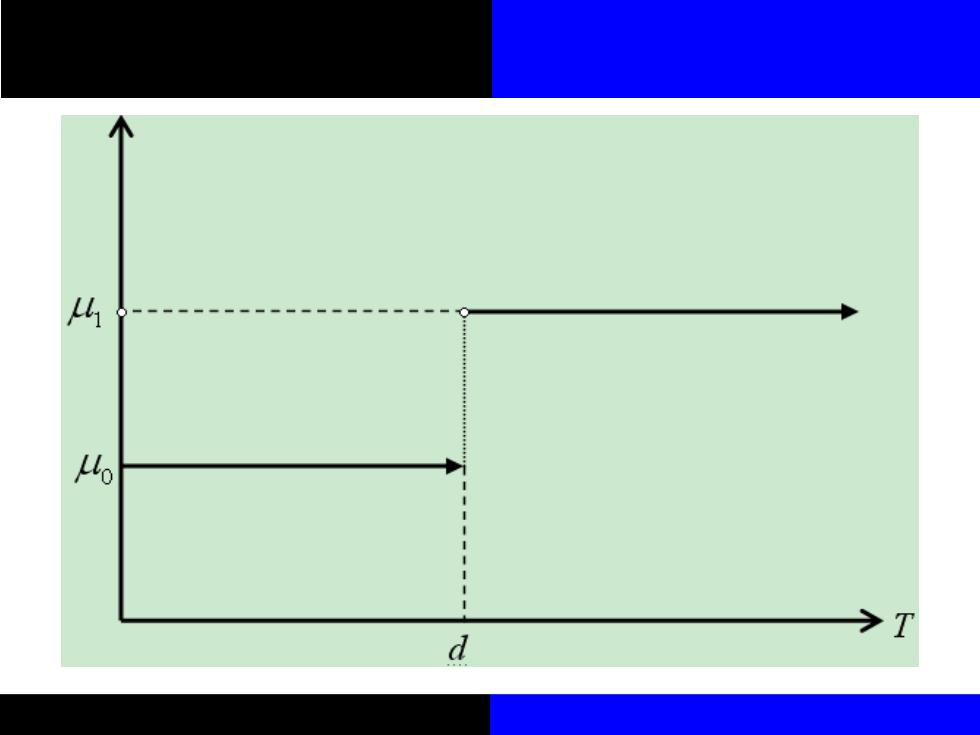
4 4 d